Chủ đề phương trình chuyển động ném ngang: Phương trình chuyển động ném ngang là một chủ đề quan trọng trong vật lý, đặc biệt hữu ích trong việc giải thích các hiện tượng trong đời sống và kỹ thuật. Bài viết này sẽ giới thiệu chi tiết về khái niệm, công thức tính toán, và bài tập ứng dụng liên quan đến chuyển động ném ngang, giúp bạn nắm vững kiến thức và áp dụng hiệu quả trong học tập cũng như thực tế.
Mục lục
- Phương trình chuyển động ném ngang
- 1. Giới thiệu về chuyển động ném ngang
- 2. Phương trình chuyển động ném ngang
- 4. Phân tích và so sánh chuyển động ném ngang với chuyển động ném xiên
- 5. Ứng dụng thực tế của chuyển động ném ngang
- 6. Bài tập vận dụng và lời giải về chuyển động ném ngang
- 7. Tài liệu tham khảo và nguồn học tập
Phương trình chuyển động ném ngang
Chuyển động ném ngang là một dạng chuyển động trong vật lý, nơi một vật được ném theo phương ngang với một vận tốc ban đầu \(v_0\). Đây là một loại chuyển động hai chiều, bao gồm chuyển động theo phương ngang (Ox) và chuyển động theo phương thẳng đứng (Oy). Dưới đây là các thông tin chi tiết liên quan đến phương trình và các đặc điểm của chuyển động ném ngang.
1. Khái niệm và đặc điểm của chuyển động ném ngang
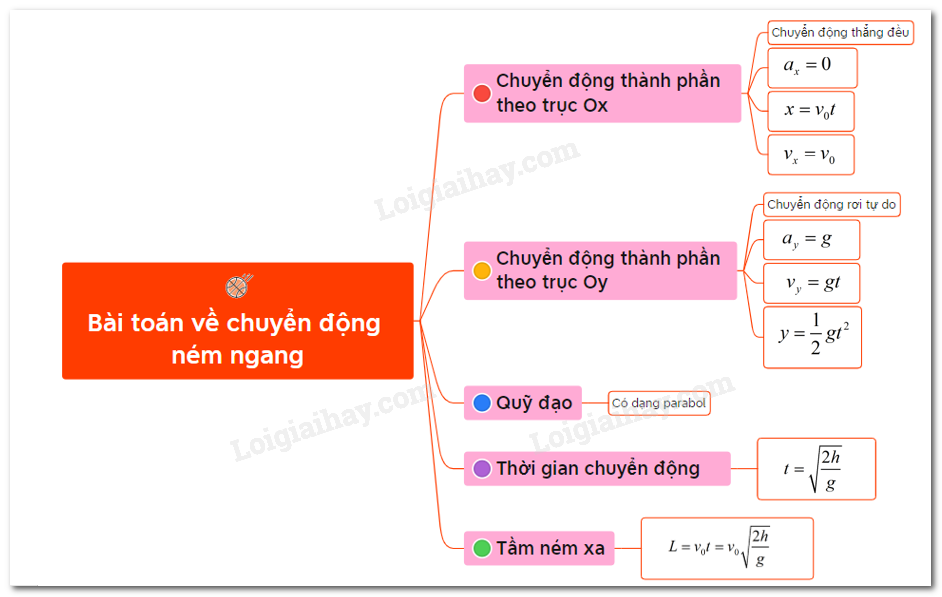
- Chuyển động ném ngang là sự kết hợp của chuyển động thẳng đều theo phương ngang và chuyển động rơi tự do theo phương thẳng đứng.
- Phương trình chuyển động theo phương ngang (Ox) được mô tả bởi:
\[
x = v_0 \cdot t
\]
trong đó:
- \(x\) là khoảng cách theo phương ngang
- \(v_0\) là vận tốc ban đầu theo phương ngang
- \(t\) là thời gian chuyển động
- Phương trình chuyển động theo phương thẳng đứng (Oy) là chuyển động rơi tự do dưới tác dụng của trọng lực, được mô tả bởi:
\[
y = \frac{1}{2} g t^2
\]
trong đó:
- \(y\) là độ cao rơi theo phương thẳng đứng
- \(g\) là gia tốc trọng trường (thường lấy \(g = 9.8 \, m/s^2\))
- \(t\) là thời gian rơi
2. Quỹ đạo của vật ném ngang
Quỹ đạo của vật ném ngang là một đường parabol. Kết hợp hai phương trình chuyển động theo phương ngang và phương thẳng đứng, ta có phương trình quỹ đạo của chuyển động ném ngang:
Phương trình này cho thấy rằng khi vật được ném ngang, nó sẽ di chuyển theo một quỹ đạo parabol trong mặt phẳng đứng.
3. Các yếu tố ảnh hưởng đến chuyển động ném ngang
- Vận tốc ném ban đầu (\(v_0\)): Vận tốc này xác định quãng đường đi được theo phương ngang trước khi vật chạm đất.
- Độ cao ban đầu (\(h\)): Độ cao từ nơi ném đến mặt đất sẽ ảnh hưởng đến thời gian rơi và do đó, ảnh hưởng đến quãng đường theo phương ngang.
- Gia tốc trọng trường (\(g\)): Ảnh hưởng trực tiếp đến chuyển động theo phương thẳng đứng.
4. Ví dụ minh họa
Giả sử một vật được ném theo phương ngang từ độ cao \(h = 20 \, m\) với vận tốc ban đầu \(v_0 = 15 \, m/s\). Tính thời gian rơi và khoảng cách theo phương ngang mà vật đi được.
- Thời gian rơi: Sử dụng phương trình \(y = \frac{1}{2} g t^2\), ta có: \[ 20 = \frac{1}{2} \cdot 9.8 \cdot t^2 \implies t \approx 2.02 \, s \]
- Khoảng cách theo phương ngang: Sử dụng phương trình \(x = v_0 \cdot t\), ta có: \[ x = 15 \cdot 2.02 \approx 30.3 \, m \]
5. Ứng dụng của chuyển động ném ngang
Chuyển động ném ngang có nhiều ứng dụng trong thực tế và khoa học, ví dụ như:
- Thiết kế quỹ đạo của đạn pháo, bóng đá, hoặc bất kỳ vật thể nào được ném theo phương ngang.
- Tính toán quỹ đạo của các vật thể trong các trò chơi thể thao, như bóng rổ hoặc bóng chày.
- Ứng dụng trong các bài toán kỹ thuật như thiết kế cầu, xây dựng, và trong nhiều lĩnh vực khoa học khác.
Kết luận
Phương trình chuyển động ném ngang cung cấp một cái nhìn sâu sắc về các nguyên tắc cơ bản của vật lý chuyển động. Hiểu rõ về nó giúp chúng ta áp dụng vào nhiều tình huống thực tế và phát triển các giải pháp kỹ thuật hiệu quả.

.png)
1. Giới thiệu về chuyển động ném ngang
Chuyển động ném ngang là một loại chuyển động trong cơ học, thuộc phần cơ học Newton, được nghiên cứu rộng rãi trong các chương trình vật lý phổ thông và đại học. Đây là chuyển động của một vật khi nó được ném theo phương ngang với vận tốc ban đầu \(v_0\), dưới tác dụng của trọng lực. Trong chuyển động này, vật chịu tác dụng của hai thành phần chuyển động:
- Chuyển động thẳng đều theo phương ngang (Ox): Vật chuyển động với vận tốc không đổi \(v_0\) do không có lực nào tác dụng lên nó theo phương ngang (bỏ qua sức cản của không khí).
- Chuyển động rơi tự do theo phương thẳng đứng (Oy): Dưới tác dụng của trọng lực, vật sẽ chuyển động với gia tốc \(g\) theo phương thẳng đứng. Phương trình mô tả chuyển động này là:
\[
y = \frac{1}{2}gt^2
\]
trong đó:
- \(y\) là khoảng cách rơi theo phương thẳng đứng
- \(g\) là gia tốc trọng trường (khoảng \(9.8 \, m/s^2\))
- \(t\) là thời gian rơi
Khi kết hợp hai chuyển động trên, quỹ đạo của vật ném ngang sẽ là một đường parabol. Phương trình tổng quát mô tả quỹ đạo của chuyển động ném ngang được viết dưới dạng:
Trong phương trình này, \(x\) là khoảng cách di chuyển theo phương ngang và \(y\) là khoảng cách di chuyển theo phương thẳng đứng.
Chuyển động ném ngang có nhiều ứng dụng trong thực tế, bao gồm tính toán quỹ đạo của các vật thể trong thể thao, kỹ thuật quân sự, và cả trong nghiên cứu khoa học. Việc hiểu rõ chuyển động này giúp chúng ta phân tích và dự đoán các tình huống khác nhau khi một vật được ném ra từ một độ cao nào đó với vận tốc ban đầu theo phương ngang.
2. Phương trình chuyển động ném ngang
Phương trình chuyển động ném ngang mô tả quỹ đạo của một vật thể khi nó được ném theo phương ngang với một vận tốc ban đầu. Trong chuyển động ném ngang, vật thể chuyển động theo hai chiều: chiều ngang (Ox) và chiều thẳng đứng (Oy). Các phương trình chuyển động này giúp ta tính toán và dự đoán được vị trí của vật thể tại bất kỳ thời điểm nào.
2.1. Phương trình chuyển động theo phương ngang (Ox)
Chuyển động theo phương ngang là chuyển động thẳng đều với vận tốc không đổi \(v_0\). Phương trình mô tả vị trí của vật thể theo thời gian \(t\) là:
- \(x\): Khoảng cách theo phương ngang từ vị trí ban đầu.
- \(v_0\): Vận tốc ban đầu theo phương ngang.
- \(t\): Thời gian chuyển động.
2.2. Phương trình chuyển động theo phương thẳng đứng (Oy)
Chuyển động theo phương thẳng đứng là chuyển động rơi tự do với gia tốc \(g\) do trọng lực. Phương trình mô tả vị trí của vật thể theo thời gian \(t\) là:
- \(y\): Độ cao rơi theo phương thẳng đứng từ vị trí ban đầu.
- \(g\): Gia tốc trọng trường (thường lấy \(g = 9.8 \, m/s^2\)).
- \(t\): Thời gian rơi.
2.3. Phương trình quỹ đạo của chuyển động ném ngang
Quỹ đạo của chuyển động ném ngang là một đường parabol. Để tìm phương trình quỹ đạo, ta kết hợp hai phương trình chuyển động theo phương ngang và phương thẳng đứng. Bằng cách loại bỏ biến thời gian \(t\), ta có:
Thay giá trị của \(t\) vào phương trình chuyển động theo phương thẳng đứng:
Phương trình này cho thấy quỹ đạo của vật ném ngang là một parabol, với chiều cao \(y\) tỉ lệ thuận với bình phương của khoảng cách ngang \(x\).
2.4. Tầm xa của chuyển động ném ngang
Tầm xa là khoảng cách xa nhất theo phương ngang mà vật thể có thể đạt được trước khi chạm đất. Tầm xa được tính khi \(y = h\) (với \(h\) là độ cao ban đầu) và có thể được tính bằng cách tìm thời gian \(t\) khi \(y = h\):
Thay giá trị của \(t\) vào phương trình chuyển động theo phương ngang để tìm tầm xa \(R\):
Phương trình này giúp xác định khoảng cách xa nhất mà vật có thể đi được theo phương ngang trước khi rơi xuống mặt đất.

4. Phân tích và so sánh chuyển động ném ngang với chuyển động ném xiên
Chuyển động ném ngang và chuyển động ném xiên là hai loại chuyển động phổ biến trong vật lý, mỗi loại có những đặc điểm và phương trình chuyển động riêng biệt. Việc hiểu rõ sự khác nhau giữa hai loại chuyển động này giúp chúng ta nắm bắt các nguyên lý cơ bản và áp dụng chúng vào các tình huống thực tế một cách hiệu quả.
4.1. Chuyển động ném ngang
Chuyển động ném ngang xảy ra khi một vật được ném theo phương ngang với một vận tốc ban đầu nhất định và chỉ chịu tác dụng của lực trọng trường theo phương thẳng đứng. Các đặc điểm của chuyển động ném ngang bao gồm:
- Quỹ đạo: Quỹ đạo của chuyển động ném ngang là một nhánh của đường parabol.
- Phương trình chuyển động: \[ x = v_0 \cdot t \] \[ y = \frac{1}{2}gt^2 \] với \(x\) là khoảng cách theo phương ngang, \(y\) là độ cao theo phương thẳng đứng, \(v_0\) là vận tốc ban đầu theo phương ngang, và \(g\) là gia tốc trọng trường.
- Tầm xa (R): Tầm xa của chuyển động ném ngang được tính bằng công thức \(R = v_0 \cdot \sqrt{\frac{2h}{g}}\), trong đó \(h\) là độ cao ban đầu.
4.2. Chuyển động ném xiên
Chuyển động ném xiên xảy ra khi một vật được ném với một góc nhất định so với phương ngang. Vật thể di chuyển theo hai phương: ngang và thẳng đứng, tạo thành một quỹ đạo parabol. Các đặc điểm của chuyển động ném xiên bao gồm:
- Quỹ đạo: Quỹ đạo của chuyển động ném xiên cũng là một nhánh của đường parabol, nhưng khác với ném ngang, nó có cả thành phần vận tốc theo phương ngang và phương thẳng đứng.
- Phương trình chuyển động: \[ x = v_0 \cdot \cos(\theta) \cdot t \] \[ y = v_0 \cdot \sin(\theta) \cdot t - \frac{1}{2}gt^2 \] với \(v_0\) là vận tốc ban đầu, \(\theta\) là góc ném, \(x\) và \(y\) lần lượt là tọa độ theo phương ngang và phương thẳng đứng.
- Tầm xa (R): Tầm xa của chuyển động ném xiên được tính bằng công thức \(R = \frac{v_0^2 \cdot \sin(2\theta)}{g}\). Tầm xa phụ thuộc vào vận tốc ban đầu và góc ném.
- Chiều cao cực đại (H): Chiều cao cực đại mà vật đạt được trong chuyển động ném xiên được tính bằng công thức \(H = \frac{v_0^2 \cdot \sin^2(\theta)}{2g}\).
4.3. So sánh chuyển động ném ngang và ném xiên
| Đặc điểm | Chuyển động ném ngang | Chuyển động ném xiên |
|---|---|---|
| Quỹ đạo | Parabol (chỉ có thành phần theo phương ngang) | Parabol (có cả thành phần theo phương ngang và phương thẳng đứng) |
| Phương trình chuyển động |
\(x = v_0 \cdot t\) \(y = \frac{1}{2}gt^2\) |
\(x = v_0 \cdot \cos(\theta) \cdot t\) \(y = v_0 \cdot \sin(\theta) \cdot t - \frac{1}{2}gt^2\) |
| Tầm xa (R) | \(R = v_0 \cdot \sqrt{\frac{2h}{g}}\) | \(R = \frac{v_0^2 \cdot \sin(2\theta)}{g}\) |
| Yếu tố ảnh hưởng | Độ cao, vận tốc ban đầu | Vận tốc ban đầu, góc ném |
| Chiều cao cực đại (H) | Không có | \(H = \frac{v_0^2 \cdot \sin^2(\theta)}{2g}\) |
Nhìn chung, chuyển động ném ngang và chuyển động ném xiên đều có quỹ đạo parabol, nhưng chúng khác nhau về cách vật thể di chuyển và các yếu tố ảnh hưởng đến chuyển động. Chuyển động ném ngang đơn giản hơn, chỉ có thành phần vận tốc theo phương ngang, trong khi chuyển động ném xiên phức tạp hơn, bao gồm cả thành phần vận tốc theo phương ngang và phương thẳng đứng.
5. Ứng dụng thực tế của chuyển động ném ngang
Chuyển động ném ngang không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng trong thực tế, đặc biệt là trong các lĩnh vực thể thao, kỹ thuật, và giáo dục. Dưới đây là một số ứng dụng nổi bật:
5.1. Ứng dụng trong thể thao
- Ném bóng rổ: Khi cầu thủ thực hiện cú ném từ xa, quả bóng sẽ di chuyển theo quỹ đạo ném ngang trước khi rơi xuống rổ. Kỹ thuật này đòi hỏi sự chính xác và tính toán quỹ đạo bay của bóng để đạt được mục tiêu.
- Phóng dao: Trong các cuộc thi phóng dao, dao sẽ di chuyển theo quỹ đạo ném ngang. Độ chính xác của phóng dao phụ thuộc vào khả năng tính toán quỹ đạo của người chơi.
5.2. Ứng dụng trong kỹ thuật và công nghệ
- Đạn đạo học: Trong lĩnh vực quân sự, khi bắn đạn từ súng, viên đạn sẽ chuyển động theo quỹ đạo ném ngang trước khi rơi xuống đất. Hiểu rõ nguyên lý này giúp cải thiện độ chính xác của việc bắn đạn ở các khoảng cách khác nhau.
- Máy bay thả hàng: Khi máy bay thả hàng cứu trợ từ trên cao, các kiện hàng sẽ di chuyển theo quỹ đạo ném ngang trước khi chạm đất. Điều này giúp đảm bảo hàng hóa được thả chính xác tại vị trí mong muốn.
5.3. Ứng dụng trong giáo dục và đào tạo
- Thí nghiệm vật lý: Các thí nghiệm kiểm chứng chuyển động ném ngang, chẳng hạn như thả viên bi từ một độ cao nhất định và quan sát quỹ đạo của nó, thường được sử dụng để giảng dạy về các nguyên tắc vật lý cơ bản trong các trường học.
- Bài tập thực hành: Học sinh có thể thực hiện các bài tập liên quan đến tính toán quỹ đạo, thời gian bay, và quãng đường di chuyển của vật khi ném ngang. Điều này giúp củng cố kiến thức lý thuyết và phát triển kỹ năng phân tích.

6. Bài tập vận dụng và lời giải về chuyển động ném ngang
Dưới đây là một số bài tập vận dụng liên quan đến chuyển động ném ngang kèm theo lời giải chi tiết. Các bài tập này giúp củng cố kiến thức và ứng dụng các công thức đã học vào việc giải quyết các vấn đề thực tế.
6.1. Bài tập cơ bản
-
Bài tập 1: Một vật được ném theo phương ngang từ độ cao 50 m so với mặt đất với vận tốc ban đầu \(v_0 = 18 \, \text{m/s}\). Tính thời gian và vận tốc của vật khi chạm đất.
Lời giải:
- Thời gian rơi tự do: \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 50}{9.8}} \approx 3.19 \, \text{s} \]
- Vận tốc khi chạm đất: \[ v = \sqrt{v_0^2 + (gt)^2} = \sqrt{18^2 + (9.8 \times 3.19)^2} \approx 36.1 \, \text{m/s} \]
-
Bài tập 2: Một vật được ném theo phương ngang với vận tốc 10 m/s từ độ cao 40 m. Tính tọa độ của vật sau 2 giây và vị trí chạm đất theo phương ngang.
Lời giải:
- Tọa độ sau 2 giây: \[ x = v_0 t = 10 \times 2 = 20 \, \text{m} \], \[ y = \frac{1}{2} g t^2 = 0.5 \times 9.8 \times 2^2 = 19.6 \, \text{m} \]
- Vị trí chạm đất: \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 40}{9.8}} \approx 2.86 \, \text{s} \], \[ x = v_0 t \approx 10 \times 2.86 = 28.6 \, \text{m} \]
6.2. Bài tập nâng cao
-
Bài tập 3: Một quả bóng được ném theo phương ngang từ độ cao 80 m với vận tốc ban đầu \(v_0 = 20 \, \text{m/s}\). Sau 3 giây, vận tốc của quả bóng hợp với phương ngang một góc \(45^\circ\). Tính vận tốc ban đầu và vị trí chạm đất.
Lời giải:
- Vận tốc ban đầu: \[ v_0 = \frac{L}{\sqrt{\frac{2h}{g}}} = \frac{20}{\sqrt{\frac{2 \times 80}{9.8}}} \approx 20 \, \text{m/s} \]
- Vị trí chạm đất: \[ x = v_0 t = 20 \times 3 = 60 \, \text{m} \]
-
Bài tập 4: Một vật được ném ngang từ độ cao 9 m với vận tốc ban đầu sao cho tầm xa là 18 m. Tính vận tốc ban đầu.
Lời giải:
- Vận tốc ban đầu: \[ v_0 = \frac{L}{\sqrt{\frac{2h}{g}}} = \frac{18}{\sqrt{\frac{2 \times 9}{10}}} \approx 10 \, \text{m/s} \]
6.3. Hướng dẫn giải chi tiết
Các bài tập trên không chỉ giúp nắm vững lý thuyết mà còn rèn luyện kỹ năng phân tích và giải quyết vấn đề. Đối với mỗi bài tập, bạn nên:
- Xác định đúng các thông số đầu vào: độ cao, vận tốc ban đầu, gia tốc trọng trường.
- Chọn hệ trục tọa độ và viết các phương trình chuyển động tương ứng.
- Giải phương trình để tìm ra các đại lượng cần tính, như thời gian, tọa độ, vận tốc.
- Sử dụng MathJax để đảm bảo các công thức toán học được hiển thị chính xác và rõ ràng.
Thực hiện bài tập nhiều lần sẽ giúp bạn nâng cao kỹ năng và tự tin hơn trong việc giải quyết các vấn đề liên quan đến chuyển động ném ngang.
XEM THÊM:
7. Tài liệu tham khảo và nguồn học tập
Để học tập và nghiên cứu sâu hơn về chuyển động ném ngang, dưới đây là một số tài liệu tham khảo và nguồn học tập hữu ích:
7.1. Sách giáo khoa và tài liệu tham khảo
- Sách giáo khoa Vật lý lớp 10: Đây là tài liệu cơ bản, cung cấp nền tảng lý thuyết về chuyển động ném ngang cùng với các bài tập vận dụng từ cơ bản đến nâng cao.
- Giáo trình Vật lý đại cương: Cung cấp kiến thức nâng cao và các phương pháp giải bài tập phức tạp về chuyển động ném ngang.
- Các sách bài tập chuyên sâu: Một số cuốn sách tập trung vào bài tập về chuyển động ném ngang, giúp rèn luyện kỹ năng giải bài tập thực tế.
7.2. Các trang web giáo dục uy tín
- : Một trang web cung cấp nhiều tài liệu học tập, trong đó có các bài giảng và bài tập về chuyển động ném ngang, ném xiên.
- : Trang web tổng hợp các bài giảng điện tử và giáo án Vật lý, bao gồm các bài giảng chi tiết về chuyển động ném ngang.
- : Trang web chia sẻ nhiều tài liệu học tập từ sách giáo khoa đến các bài tập nâng cao và giáo trình đại học.
7.3. Video và khóa học trực tuyến
- Youtube: Có nhiều kênh giáo dục cung cấp video giảng dạy về chuyển động ném ngang, giải thích chi tiết từng bước giải bài tập.
- Coursera và edX: Các nền tảng này cung cấp khóa học trực tuyến về Vật lý cơ bản, trong đó có nội dung về chuyển động ném ngang.
Các tài liệu và nguồn học tập trên sẽ hỗ trợ bạn nắm vững lý thuyết và kỹ năng giải bài tập về chuyển động ném ngang một cách hiệu quả.