Chủ đề chuyển động quay của vật rắn: Chuyển động quay của vật rắn là một khái niệm quan trọng trong cơ học, giúp hiểu rõ các hiện tượng tự nhiên và ứng dụng trong nhiều lĩnh vực. Bài viết này sẽ giới thiệu các kiến thức cơ bản, phương trình liên quan và những ứng dụng thực tiễn trong cuộc sống hàng ngày.
Mục lục
Chuyển Động Quay Của Vật Rắn
Chuyển động quay của vật rắn là một hiện tượng vật lý quan trọng, đặc biệt trong lĩnh vực cơ học. Đây là một loại chuyển động đặc biệt, trong đó mọi điểm trên vật rắn đều quay quanh một trục cố định.
1. Định nghĩa và khái niệm cơ bản
Chuyển động quay của vật rắn xảy ra khi tất cả các phần của vật rắn đều quay quanh một trục cố định. Trục này có thể nằm trong hoặc ngoài vật. Một ví dụ điển hình là chuyển động của bánh xe khi xe di chuyển.
2. Phương trình và đại lượng mô tả chuyển động quay
- Tốc độ góc \(\omega\): Là đại lượng mô tả tốc độ quay của vật quanh trục cố định, được tính bằng đơn vị radian trên giây (rad/s).
- Gia tốc góc \(\alpha\): Là đại lượng mô tả sự thay đổi của tốc độ góc theo thời gian, đơn vị là radian trên giây bình phương (rad/s²).
- Mômen quán tính \(I\): Là đại lượng đặc trưng cho sự phân bố khối lượng của vật rắn quanh trục quay, được tính bằng công thức: \[ I = \sum m_i r_i^2 \] trong đó \(m_i\) là khối lượng phần tử nhỏ của vật, và \(r_i\) là khoảng cách từ phần tử đó đến trục quay.
- Mômen lực \(M\): Là đại lượng đặc trưng cho tác động làm vật quay quanh trục, được tính bằng công thức: \[ M = I\alpha \] trong đó \(M\) là mômen lực, \(I\) là mômen quán tính và \(\alpha\) là gia tốc góc.
3. Các loại chuyển động quay
- Chuyển động quay đều: Là loại chuyển động mà tốc độ góc của vật không đổi theo thời gian, tức là \(\alpha = 0\).
- Chuyển động quay biến đổi đều: Là chuyển động trong đó gia tốc góc \(\alpha\) là hằng số, làm tốc độ góc thay đổi đều theo thời gian.
4. Các ứng dụng của chuyển động quay
Chuyển động quay của vật rắn có nhiều ứng dụng quan trọng trong thực tế, từ việc vận hành các thiết bị cơ khí, động cơ đến các hiện tượng thiên văn như sự quay của các hành tinh quanh mặt trời.
5. Bài toán và ví dụ minh họa
Để hiểu rõ hơn về chuyển động quay, ta có thể xét một ví dụ đơn giản: Tính mômen quán tính của một bánh xe có khối lượng 2kg và bán kính 0.5m quay quanh trục của nó.
Công thức tính mômen quán tính:
\[
I = m r^2
\]
Thay số ta được:
\[
I = 2 \times 0.5^2 = 0.5 \text{ kg.m}^2
\]
6. Kết luận
Chuyển động quay của vật rắn là một phần không thể thiếu trong cơ học, giúp chúng ta hiểu rõ hơn về cách thức các vật thể di chuyển và tương tác trong thế giới tự nhiên.

.png)
1. Khái Niệm Cơ Bản Về Chuyển Động Quay Của Vật Rắn
Chuyển động quay của vật rắn là một dạng chuyển động trong đó mọi điểm của vật đều di chuyển trên những quỹ đạo tròn, có tâm nằm trên một đường thẳng gọi là trục quay. Đây là hiện tượng thường thấy trong tự nhiên và kỹ thuật, đóng vai trò quan trọng trong nhiều lĩnh vực như cơ khí, điện tử và thiên văn học.
1.1 Định nghĩa chuyển động quay
Chuyển động quay của vật rắn được định nghĩa là chuyển động của một vật khi nó quay xung quanh một trục cố định. Trong chuyển động này, các phần tử của vật rắn sẽ có vận tốc khác nhau tùy thuộc vào khoảng cách của chúng đến trục quay.
1.2 Các đại lượng đặc trưng trong chuyển động quay
- Góc quay \(\theta\): Là góc mà vật rắn quay quanh trục, đo bằng radian.
- Tốc độ góc \(\omega\): Là đại lượng đo sự thay đổi của góc quay theo thời gian, đơn vị là radian/giây \(\left(\text{rad/s}\right)\).
- Gia tốc góc \(\alpha\): Là đại lượng đo sự thay đổi của tốc độ góc theo thời gian, đơn vị là radian/giây bình phương \(\left(\text{rad/s}^2\right)\).
- Mômen quán tính \(I\): Là đại lượng đặc trưng cho sự phân bố khối lượng của vật rắn xung quanh trục quay, công thức tổng quát là \[I = \sum m_i r_i^2\], trong đó \(m_i\) là khối lượng của phần tử thứ \(i\), và \(r_i\) là khoảng cách từ phần tử đó đến trục quay.
1.3 Phân loại chuyển động quay
Chuyển động quay có thể được phân loại dựa trên sự ổn định của trục quay và tốc độ quay:
- Chuyển động quay đều: Khi tốc độ góc \(\omega\) của vật rắn không thay đổi theo thời gian, tức là \(\alpha = 0\).
- Chuyển động quay không đều: Khi tốc độ góc \(\omega\) của vật rắn thay đổi theo thời gian, tức là \(\alpha \neq 0\).
- Chuyển động quay quanh trục cố định: Trục quay của vật rắn không thay đổi vị trí trong không gian.
- Chuyển động quay quanh trục di động: Trục quay của vật rắn có thể thay đổi vị trí trong không gian, ví dụ như chuyển động precession của con quay hồi chuyển.
2. Phương Trình Và Đại Lượng Trong Chuyển Động Quay
Trong chuyển động quay của vật rắn, có nhiều phương trình và đại lượng quan trọng giúp chúng ta hiểu rõ hơn về cách vật rắn quay quanh trục cố định. Những phương trình này mô tả mối quan hệ giữa các đại lượng như góc quay, tốc độ góc, gia tốc góc, và mômen lực.
2.1 Phương trình tốc độ góc và gia tốc góc
Giống như chuyển động tịnh tiến, chuyển động quay cũng có các phương trình mô tả sự thay đổi của tốc độ và gia tốc:
- Tốc độ góc \(\omega\): Là đại lượng mô tả tốc độ thay đổi góc quay theo thời gian, được tính bằng công thức: \[ \omega = \frac{d\theta}{dt} \] trong đó \(\theta\) là góc quay, \(t\) là thời gian.
- Gia tốc góc \(\alpha\): Là đại lượng mô tả tốc độ thay đổi của tốc độ góc theo thời gian, được tính bằng công thức: \[ \alpha = \frac{d\omega}{dt} = \frac{d^2\theta}{dt^2} \]
2.2 Mômen quán tính và các yếu tố ảnh hưởng
Mômen quán tính \(I\) là một đại lượng quan trọng trong chuyển động quay, đặc trưng cho sự phân bố khối lượng của vật rắn quanh trục quay. Nó được tính theo công thức:
trong đó:
- \(m_i\) là khối lượng của phần tử thứ \(i\) trong vật rắn.
- \(r_i\) là khoảng cách từ phần tử \(i\) đến trục quay.
Các yếu tố ảnh hưởng đến mômen quán tính bao gồm khối lượng của vật và cách phân bố khối lượng đó xung quanh trục quay. Vật có khối lượng phân bố càng xa trục quay thì mômen quán tính càng lớn.
2.3 Mômen lực và phương trình động lực học
Mômen lực \(\tau\) là đại lượng đặc trưng cho khả năng gây ra chuyển động quay của một lực tác dụng lên vật rắn. Nó được tính bằng công thức:
trong đó:
- \(r\) là khoảng cách từ trục quay đến điểm đặt lực.
- \(F\) là độ lớn của lực tác dụng.
- \(\theta\) là góc giữa vector lực và vector khoảng cách.
Phương trình động lực học của chuyển động quay được mô tả bằng công thức:
Trong đó, \(\tau\) là mômen lực, \(I\) là mômen quán tính và \(\alpha\) là gia tốc góc. Phương trình này tương tự như định luật II Newton cho chuyển động tịnh tiến, trong đó lực được thay bằng mômen lực, khối lượng được thay bằng mômen quán tính, và gia tốc tịnh tiến được thay bằng gia tốc góc.

3. Ứng Dụng Của Chuyển Động Quay
Chuyển động quay của vật rắn không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tế trong đời sống hàng ngày, từ các lĩnh vực công nghiệp, thiên văn học cho đến cơ khí và công nghệ. Dưới đây là một số ứng dụng tiêu biểu của chuyển động quay:
3.1 Trong cơ khí và động cơ
Các bộ phận như bánh răng, trục, và bánh xe trong các hệ thống cơ khí đều hoạt động dựa trên nguyên lý của chuyển động quay. Đặc biệt, trong các động cơ đốt trong, piston di chuyển tạo ra chuyển động tịnh tiến, sau đó được chuyển đổi thành chuyển động quay để vận hành trục khuỷu, từ đó dẫn động các bánh xe.
- Ví dụ: Bánh đà trong động cơ xe hơi giúp lưu trữ năng lượng dưới dạng động năng quay, giúp duy trì tốc độ ổn định.
- Các hệ thống băng tải trong nhà máy sử dụng các trục quay để di chuyển sản phẩm từ điểm này sang điểm khác một cách hiệu quả.
3.2 Trong thiên văn học
Chuyển động quay là hiện tượng tự nhiên phổ biến trong vũ trụ. Các hành tinh quay quanh trục của mình và quanh mặt trời tạo ra các chu kỳ ngày và đêm, mùa và năm.
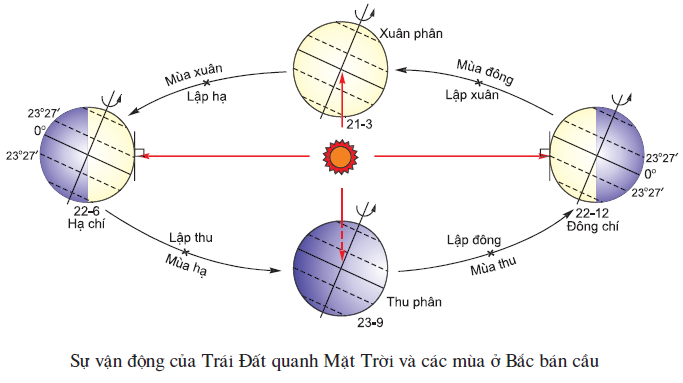
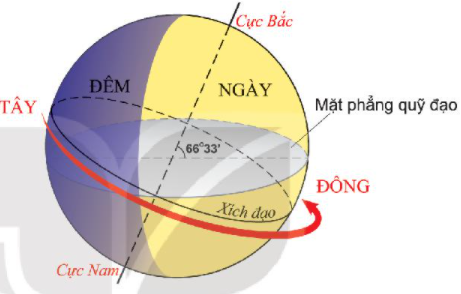
- Ví dụ: Trái Đất quay quanh trục tạo ra ngày và đêm, trong khi quay quanh mặt trời tạo ra các mùa trong năm.
- Sự quay của các thiên thể lớn như sao và hành tinh còn ảnh hưởng đến quỹ đạo của các vật thể nhỏ hơn trong không gian.
3.3 Trong đời sống hàng ngày
Chuyển động quay có thể được quan sát dễ dàng trong các thiết bị hàng ngày như quạt, máy giặt, và cả trong các môn thể thao.
- Ví dụ: Trong các trận bóng đá, chuyển động quay của quả bóng tạo ra hiện tượng "xoáy" khiến đường đi của bóng trở nên khó dự đoán.
- Các thiết bị gia dụng như máy giặt sử dụng nguyên lý quay để giặt và vắt quần áo.

4. Bài Tập Và Ví Dụ Minh Họa
Dưới đây là một số bài tập và ví dụ minh họa về chuyển động quay của vật rắn. Những bài tập này giúp bạn nắm vững các khái niệm và công thức liên quan đến chuyển động quay, từ tính mômen quán tính cho đến việc áp dụng phương trình động lực học.
4.1 Tính mômen quán tính của các vật thể đơn giản
Mômen quán tính \(I\) của một vật thể rắn đối với một trục quay là đại lượng quan trọng để đặc trưng cho mức độ khó khăn khi làm vật thể đó quay. Công thức chung cho mômen quán tính là:
Với \(m_i\) là khối lượng của phần tử \(i\) và \(r_i\) là khoảng cách từ phần tử đó đến trục quay. Ví dụ, tính mômen quán tính của một thanh đồng nhất dài \(L\) quay quanh một trục nằm ngang đi qua đầu thanh:
4.2 Giải bài toán về mômen lực
Mômen lực \(\tau\) được định nghĩa là tích của lực \(F\) và cánh tay đòn \(r\):
Ví dụ: Một lực \(F = 10N\) tác dụng lên một điểm trên vật rắn với cánh tay đòn \(r = 0.5m\) và góc giữa lực và cánh tay đòn là \(90^\circ\). Mômen lực tác dụng lên vật rắn là:
4.3 Phân tích chuyển động quay của các hệ thống phức tạp
Trong các hệ thống phức tạp, ta cần sử dụng nhiều công thức và phương pháp khác nhau để phân tích chuyển động quay. Một ví dụ là hệ thống gồm nhiều đĩa quay với các mômen quán tính khác nhau. Để phân tích chuyển động, ta sử dụng phương trình động lực học:
Trong đó, \(\alpha\) là gia tốc góc của hệ thống. Nếu hệ thống chịu tác động của nhiều mômen lực, ta cộng các mômen lực lại để tìm tổng mômen tác dụng lên hệ thống.
Những bài tập và ví dụ này không chỉ giúp bạn củng cố kiến thức về chuyển động quay mà còn ứng dụng trong các lĩnh vực thực tiễn như cơ khí và kỹ thuật.

5. Các Công Cụ Hỗ Trợ Học Tập Và Mô Phỏng
Để hỗ trợ việc học và nghiên cứu về chuyển động quay của vật rắn, có rất nhiều công cụ và phần mềm mô phỏng hữu ích mà bạn có thể sử dụng. Các công cụ này không chỉ giúp trực quan hóa các khái niệm phức tạp mà còn cung cấp môi trường thực hành thực tế.
5.1. Phần Mềm Mô Phỏng Chuyển Động
- Matlab: Đây là một công cụ mạnh mẽ cho việc mô phỏng và phân tích chuyển động của vật rắn, cho phép bạn thực hiện các bài toán động lực học và kiểm tra các kết quả một cách trực quan.
- Python với Thư Viện NumPy và Matplotlib: Python là một lựa chọn tuyệt vời khác với các thư viện hỗ trợ tính toán và vẽ đồ thị, giúp mô phỏng chuyển động quay với độ chính xác cao.
5.2. Các Mô Phỏng Tương Tác Trực Quan
Các phần mềm trực quan và tương tác là cách tốt nhất để nắm vững các khái niệm về chuyển động quay:
- Stellarium: Phần mềm bản đồ sao này có thể được sử dụng để nghiên cứu về chuyển động quay trong thiên văn học, giúp học sinh hiểu rõ hơn về quỹ đạo và tốc độ quay của các hành tinh.
- Stuff in Space: Công cụ này cho phép theo dõi và mô phỏng quỹ đạo vệ tinh trong không gian, một ứng dụng thực tế của chuyển động quay.
5.3. Các Bài Tập Mô Phỏng
Việc áp dụng các mô phỏng vào bài tập là một cách tuyệt vời để thực hành và củng cố kiến thức:
- Sử dụng Matlab để mô phỏng chuyển động quay của một vật rắn quanh trục cố định và phân tích các đại lượng như tốc độ góc \(\omega\) và gia tốc góc \(\alpha\).
- Sử dụng Python để tạo đồ thị biểu diễn sự thay đổi của vận tốc và gia tốc của một điểm trên vật rắn trong quá trình quay, với các phương trình mô tả:
- Ví dụ, phương trình vận tốc dài \(v\) của một điểm trên vật rắn là \(v = \omega r\), với \(r\) là bán kính quỹ đạo của điểm đó.
XEM THÊM:
6. Kết Luận
Chuyển động quay của vật rắn quanh một trục cố định là một hiện tượng quan trọng trong vật lý, liên quan đến nhiều yếu tố như tốc độ góc, mômen lực, và mức quán tính. Qua việc nghiên cứu, ta thấy rằng mọi vật quay quanh một trục đều có mức quán tính riêng, phụ thuộc vào khối lượng và sự phân bố khối lượng của vật.
Trong quá trình học tập và nghiên cứu về chuyển động quay của vật rắn, việc hiểu rõ các định luật Newton và áp dụng đúng vào từng trường hợp cụ thể là rất quan trọng. Điều này không chỉ giúp hiểu sâu hơn về các hiện tượng vật lý mà còn hỗ trợ trong việc giải quyết các bài toán liên quan.
Việc áp dụng thực tiễn từ các bài toán và mô phỏng chuyển động quay giúp học sinh nắm vững hơn về cách hoạt động của các cơ chế trong cuộc sống hàng ngày, từ bánh xe cho đến động cơ.
Qua đây, có thể kết luận rằng, việc nắm bắt các kiến thức cơ bản về chuyển động quay của vật rắn sẽ là nền tảng quan trọng để học sinh phát triển các kỹ năng giải quyết vấn đề và ứng dụng vào thực tiễn.