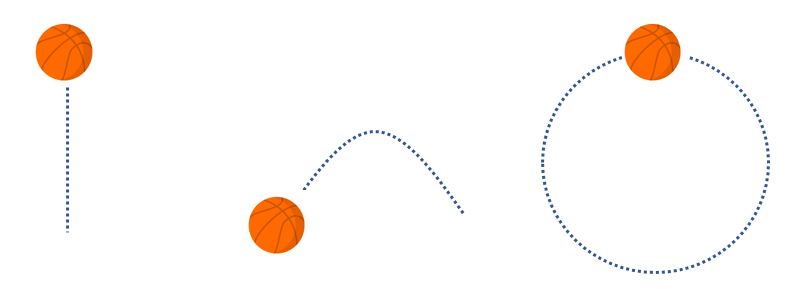
Chủ đề một vật đang chuyển động với vận tốc 3m/s: Một vật đang chuyển động với vận tốc 3m/s là một khái niệm cơ bản trong vật lý học, liên quan đến chuyển động thẳng đều và các định luật Newton. Bài viết này sẽ giúp bạn hiểu rõ hơn về định nghĩa, ứng dụng thực tế và các yếu tố ảnh hưởng đến chuyển động của một vật khi nó duy trì vận tốc cố định, giúp bạn nắm bắt được các khái niệm vật lý một cách dễ dàng và thực tế.
Mục lục
- Thông Tin Về Chuyển Động Vật Lý Với Vận Tốc 3 m/s
- Tổng Quan Về Chuyển Động Thẳng Đều
- Phân Tích Chuyển Động Của Một Vật Với Vận Tốc 3m/s
- Định Luật Bảo Toàn Động Lượng
- Ứng Dụng Thực Tế Của Chuyển Động Thẳng Đều
- Thực Hành Và Bài Tập Liên Quan
- Những Khái Niệm Liên Quan Đến Vận Tốc Và Gia Tốc
- Tài Liệu Tham Khảo Và Nguồn Học Tập
Thông Tin Về Chuyển Động Vật Lý Với Vận Tốc 3 m/s
Khi nghiên cứu về vật lý, việc tìm hiểu về chuyển động của các vật thể đóng vai trò quan trọng trong việc hiểu các khái niệm cơ bản của cơ học. Một trong những ví dụ thường gặp là một vật đang chuyển động với vận tốc 3 m/s. Dưới đây là tổng hợp các thông tin liên quan đến chủ đề này.
1. Định Nghĩa Vận Tốc
Vận tốc là đại lượng vector biểu diễn độ nhanh và hướng của chuyển động của một vật. Đơn vị vận tốc thường được sử dụng là mét trên giây (m/s). Vận tốc có thể được xác định bằng công thức:
\[
v = \frac{s}{t}
\]
trong đó:
- \(v\): Vận tốc (m/s)
- \(s\): Quãng đường đi được (m)
- \(t\): Thời gian (s)
2. Chuyển Động Thẳng Đều
Một vật chuyển động với vận tốc không đổi được gọi là chuyển động thẳng đều. Trong trường hợp này, vật di chuyển với vận tốc 3 m/s là một ví dụ về chuyển động thẳng đều. Vận tốc này có nghĩa là vật sẽ di chuyển một quãng đường 3 mét trong mỗi giây.
- Định luật 1 Newton: Nếu không có lực nào tác dụng lên vật, hoặc các lực tác dụng lên vật cân bằng, thì vật đang chuyển động sẽ tiếp tục chuyển động thẳng đều.
- Ví dụ: Nếu một vật đang chuyển động với vận tốc 3 m/s và không chịu tác dụng của bất kỳ lực nào, nó sẽ tiếp tục chuyển động với vận tốc này.
3. Ảnh Hưởng Của Các Lực Đối Với Chuyển Động
Nếu các lực tác dụng lên vật, như lực ma sát hoặc lực cản, chúng có thể thay đổi vận tốc của vật. Ví dụ:
- Nếu một lực ma sát tác dụng ngược chiều với hướng chuyển động, nó sẽ làm giảm vận tốc của vật từ 3 m/s.
- Nếu có lực tác dụng cùng chiều với chuyển động, vận tốc của vật có thể tăng lên từ 3 m/s.
Vận tốc có thể thay đổi theo các định luật Newton khác, bao gồm định luật 2 và 3 Newton.
4. Ứng Dụng Thực Tiễn
Hiểu về vận tốc và chuyển động thẳng đều có nhiều ứng dụng trong đời sống thực tiễn:
- Trong giao thông, vận tốc của xe cộ được đo và giám sát để đảm bảo an toàn.
- Trong thể thao, vận động viên cần duy trì một vận tốc cụ thể để đạt được thành tích tốt nhất.
- Trong kỹ thuật, các kỹ sư thiết kế máy móc cần tính toán vận tốc để đảm bảo hiệu suất và an toàn.
5. Bài Tập Liên Quan Đến Vận Tốc
Các bài tập vật lý thường yêu cầu học sinh tính toán vận tốc, quãng đường hoặc thời gian dựa trên các dữ liệu cho trước. Ví dụ, nếu một vật đang chuyển động với vận tốc 3 m/s và ta biết thời gian chuyển động là 5 giây, ta có thể tính được quãng đường:
\[
s = v \times t = 3 \, \text{m/s} \times 5 \, \text{s} = 15 \, \text{m}
\]
6. Kết Luận
Vận tốc là một khái niệm cơ bản trong vật lý học, giúp ta hiểu rõ hơn về cách các vật thể chuyển động. Việc nắm vững kiến thức về vận tốc và các nguyên tắc liên quan sẽ hỗ trợ trong nhiều lĩnh vực khoa học và ứng dụng thực tiễn.
.png)
Tổng Quan Về Chuyển Động Thẳng Đều
Chuyển động thẳng đều là chuyển động của một vật khi nó di chuyển theo một đường thẳng với vận tốc không đổi. Trong quá trình này, vật không chịu ảnh hưởng của lực nào thay đổi vận tốc, do đó gia tốc của vật bằng 0.
- Định nghĩa: Chuyển động thẳng đều là chuyển động mà trong đó vật di chuyển theo đường thẳng với vận tốc không đổi theo thời gian.
- Công thức tính vận tốc: Vận tốc trong chuyển động thẳng đều được xác định bằng công thức:
\[
v = \frac{s}{t}
\]
trong đó:
- \(v\) là vận tốc (m/s).
- \(s\) là quãng đường đi được (m).
- \(t\) là thời gian đi hết quãng đường đó (s).
- Đặc điểm:
- Quỹ đạo di chuyển của vật là một đường thẳng.
- Vận tốc của vật luôn không đổi về cả độ lớn và hướng.
- Gia tốc của vật bằng 0, nghĩa là không có sự thay đổi về tốc độ hay hướng của vật.
- Ứng dụng trong thực tế: Chuyển động thẳng đều xuất hiện trong nhiều tình huống đời sống như xe chạy đều trên đường cao tốc, dòng nước chảy đều trong kênh mương, hay vệ tinh quay quanh Trái Đất trong quỹ đạo tròn đều.
- Phân biệt với các loại chuyển động khác:
- Chuyển động thẳng biến đổi đều: Vật di chuyển theo đường thẳng nhưng có vận tốc thay đổi (có gia tốc).
- Chuyển động cong: Vật di chuyển theo quỹ đạo cong và có sự thay đổi về hướng vận tốc.
Việc hiểu rõ chuyển động thẳng đều giúp giải quyết các bài toán vật lý liên quan đến tính toán quãng đường, thời gian và vận tốc, đồng thời áp dụng vào thực tế đời sống và khoa học kỹ thuật.
Phân Tích Chuyển Động Của Một Vật Với Vận Tốc 3m/s
Chuyển động của một vật với vận tốc 3 m/s là một dạng chuyển động thẳng đều, nghĩa là vật di chuyển theo một đường thẳng với vận tốc không đổi. Để hiểu rõ hơn về chuyển động này, ta cần xem xét các yếu tố ảnh hưởng đến nó như lực tác dụng, quán tính và định luật Newton.
- Vận tốc và gia tốc: Vận tốc của vật là 3 m/s, và vì chuyển động là thẳng đều nên gia tốc của vật bằng 0. Điều này có nghĩa là không có sự thay đổi về vận tốc theo thời gian.
- Quy luật Newton: Theo định luật I Newton, nếu không có lực tác dụng, một vật đang chuyển động sẽ tiếp tục chuyển động thẳng đều. Do đó, nếu lực tác dụng lên vật mất đi, vật vẫn tiếp tục chuyển động với vận tốc ban đầu là 3 m/s.
- Ứng dụng trong thực tế: Chuyển động với vận tốc không đổi được ứng dụng trong nhiều lĩnh vực, như nghiên cứu chuyển động của các phương tiện giao thông, phân tích lực tác dụng lên vật di chuyển, hoặc mô phỏng chuyển động trong không gian.
Chuyển động thẳng đều với vận tốc 3 m/s giúp chúng ta hiểu rõ hơn về các khái niệm vật lý cơ bản, đồng thời giải thích được nhiều hiện tượng trong tự nhiên và ứng dụng trong đời sống hàng ngày.
| Thành phần | Mô tả |
|---|---|
| Vận tốc | 3 m/s (không đổi) |
| Gia tốc | 0 m/s² |
| Lực tác dụng | Không có lực tác dụng thêm (vật tiếp tục chuyển động theo định luật I Newton) |

Định Luật Bảo Toàn Động Lượng
Định luật bảo toàn động lượng phát biểu rằng: "Tổng động lượng của một hệ kín không thay đổi trong quá trình tương tác, bất kể những biến đổi nào xảy ra trong hệ thống đó". Điều này có nghĩa là trong mọi sự kiện như va chạm hoặc các quá trình khác trong một hệ kín, tổng động lượng trước và sau sự kiện vẫn giữ nguyên.
Để hiểu rõ hơn về định luật này, ta xét trường hợp của một hệ hai vật có khối lượng \(m_1\) và \(m_2\), với vận tốc ban đầu tương ứng là \(v_1\) và \(v_2\). Sau khi va chạm, chúng có vận tốc mới là \(v_1'\) và \(v_2'\). Theo định luật bảo toàn động lượng, ta có phương trình:
Trong đó:
- \(m_1\), \(m_2\): Khối lượng của vật 1 và vật 2.
- \(v_1\), \(v_2\): Vận tốc của vật 1 và vật 2 trước va chạm.
- \(v_1'\), \(v_2'\): Vận tốc của vật 1 và vật 2 sau va chạm.
Ứng Dụng Định Luật Bảo Toàn Động Lượng
Định luật bảo toàn động lượng được áp dụng rộng rãi trong các tình huống như:
- Va chạm mềm: Khi hai vật va chạm và gắn kết với nhau sau va chạm, như khi một viên đạn xuyên qua và mắc kẹt vào một tấm gỗ.
- Va chạm đàn hồi: Khi hai vật bật ngược lại sau khi va chạm, như khi hai quả bóng bàn va vào nhau mà không mất động lượng.
- Chuyển động bằng phản lực: Tên lửa khi phóng ra khí nóng phía sau sẽ tạo phản lực để di chuyển về phía trước.
Biểu Thức Động Lượng và Xung Lượng
Động lượng của một vật được xác định bằng công thức:
Trong đó:
- \(p\): Động lượng của vật (kg·m/s).
- \(m\): Khối lượng của vật (kg).
- \(v\): Vận tốc của vật (m/s).
Xung lượng của lực được định nghĩa là tích của lực \(F\) và thời gian tác dụng \(\Delta t\), và được liên hệ với biến thiên động lượng của vật:
Định luật bảo toàn động lượng có tầm quan trọng lớn trong nhiều lĩnh vực như cơ học, vũ trụ học, và kỹ thuật, giúp giải thích các hiện tượng từ va chạm giữa các vật thể nhỏ như hạt nguyên tử cho đến các vụ nổ lớn trong vũ trụ.

Ứng Dụng Thực Tế Của Chuyển Động Thẳng Đều
Chuyển động thẳng đều là một dạng chuyển động cơ bản trong vật lý, trong đó một vật thể di chuyển với vận tốc không đổi theo một đường thẳng. Ứng dụng của chuyển động thẳng đều rất phổ biến trong nhiều lĩnh vực thực tế khác nhau, từ giao thông, vận tải đến thiết kế kỹ thuật và cơ học.
- Ứng dụng trong giao thông:
Trong ngành giao thông vận tải, nguyên lý của chuyển động thẳng đều được áp dụng để điều khiển các phương tiện di chuyển với tốc độ ổn định. Ví dụ, khi một ô tô chạy trên đường cao tốc với vận tốc không đổi, nó đang thực hiện chuyển động thẳng đều. Điều này giúp giảm thiểu nguy cơ tai nạn và tối ưu hóa hiệu suất nhiên liệu.
- Ứng dụng trong kỹ thuật và công nghiệp:
Trong các hệ thống sản xuất công nghiệp, chuyển động thẳng đều được sử dụng trong các băng tải và hệ thống vận chuyển tự động. Các băng tải này chuyển các sản phẩm từ một vị trí này đến vị trí khác với tốc độ không đổi, đảm bảo quá trình sản xuất diễn ra liên tục và hiệu quả.
- Ứng dụng trong thiết kế thiết bị:
Chuyển động thẳng đều cũng được áp dụng trong thiết kế các thiết bị như thang máy, thang cuốn và các hệ thống nâng hạ. Những thiết bị này được thiết kế để di chuyển một cách đều đặn, an toàn, và tiết kiệm năng lượng khi vận chuyển người hoặc hàng hóa lên xuống các tầng khác nhau.
Chuyển động thẳng đều là một phần quan trọng trong các mô hình mô phỏng và tính toán vật lý. Việc nắm vững nguyên lý này giúp chúng ta hiểu rõ hơn về cách các vật thể di chuyển và tương tác trong thế giới thực, từ đó có thể ứng dụng vào việc thiết kế và tối ưu hóa các hệ thống và thiết bị hàng ngày.
Sử dụng các công thức vật lý, chúng ta có thể tính toán các yếu tố như quãng đường đi được và thời gian cần thiết khi biết vận tốc không đổi của vật thể. Ví dụ:
Trong đó:
- \(s\) là quãng đường đi được (mét).
- \(v\) là vận tốc không đổi (mét/giây).
- \(t\) là thời gian chuyển động (giây).
Nhờ đó, chúng ta có thể dự đoán được chuyển động và thực hiện các điều chỉnh cần thiết để đạt được hiệu suất tối ưu trong các hệ thống sử dụng chuyển động thẳng đều.

Thực Hành Và Bài Tập Liên Quan
Để hiểu rõ hơn về chuyển động thẳng đều, chúng ta có thể áp dụng các bài tập thực hành và câu hỏi liên quan. Những bài tập này sẽ giúp bạn củng cố kiến thức và kỹ năng tính toán các yếu tố như quãng đường, vận tốc, và thời gian trong chuyển động thẳng đều.
Bài Tập 1: Tính Quãng Đường Đi Được
Một vật đang chuyển động với vận tốc không đổi là \(3 \, \text{m/s}\). Hãy tính quãng đường mà vật đi được sau các khoảng thời gian sau:
- a) Sau \(5\) giây.
- b) Sau \(10\) giây.
- c) Sau \(15\) giây.
Lời giải:
Áp dụng công thức tính quãng đường:
Trong đó:
- \(v = 3 \, \text{m/s}\) (vận tốc không đổi)
- \(t\) là thời gian chuyển động (giây)
Bài Tập 2: Tính Thời Gian Chuyển Động
Một vật di chuyển quãng đường \(60\) mét với vận tốc \(3 \, \text{m/s}\). Tính thời gian cần thiết để vật đi hết quãng đường này.
Lời giải:
Sử dụng công thức:
Trong đó:
- \(s = 60 \, \text{m}\) (quãng đường)
- \(v = 3 \, \text{m/s}\) (vận tốc không đổi)
Bài Tập 3: Tính Vận Tốc
Một vật đi hết quãng đường \(150\) mét trong thời gian \(50\) giây. Hãy tính vận tốc của vật.
Lời giải:
Sử dụng công thức:
Trong đó:
- \(s = 150 \, \text{m}\) (quãng đường)
- \(t = 50 \, \text{giây}\) (thời gian)
Bài Tập Thực Hành Thực Tế
Bạn có thể thực hiện các bài tập thực tế bằng cách sử dụng đồng hồ bấm giờ và một đoạn đường đã biết trước quãng đường. Di chuyển với tốc độ đều và đo thời gian để tính vận tốc. Thử lặp lại nhiều lần để thấy sự khác biệt và tính chính xác trong kết quả đo lường.
Các bài tập trên giúp bạn nắm vững cách tính toán và ứng dụng định luật chuyển động thẳng đều trong các tình huống thực tế. Hãy tự thực hành và kiểm tra lại kết quả của mình để hiểu rõ hơn về nguyên lý vật lý này.
XEM THÊM:
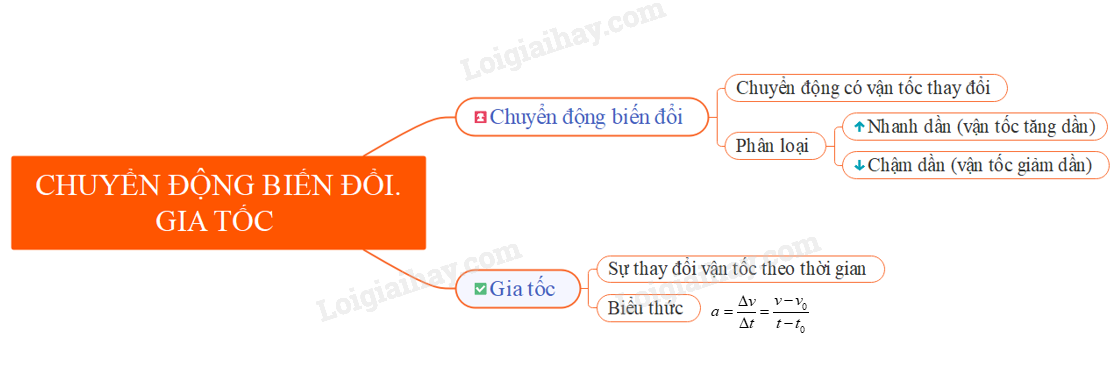
Những Khái Niệm Liên Quan Đến Vận Tốc Và Gia Tốc
Trong chuyển động, vận tốc và gia tốc là hai khái niệm cơ bản nhưng dễ nhầm lẫn nếu không hiểu rõ. Cùng tìm hiểu kỹ hơn về hai đại lượng này và cách chúng tương tác trong chuyển động thẳng đều.
Vận tốc: Định nghĩa và Công thức tính toán
Vận tốc là đại lượng vector thể hiện sự thay đổi vị trí của một vật theo thời gian. Đơn vị của vận tốc trong hệ SI là mét trên giây (m/s). Vận tốc có thể được xác định bằng công thức:
\[ v = \frac{\Delta s}{\Delta t} \]
Trong đó:
- \( v \) là vận tốc của vật (m/s)
- \( \Delta s \) là quãng đường đi được (m)
- \( \Delta t \) là khoảng thời gian (s)
Gia tốc: Khái niệm và Phân biệt với Vận tốc
Gia tốc cũng là một đại lượng vector, nhưng nó thể hiện sự thay đổi vận tốc của một vật theo thời gian. Gia tốc được tính bằng công thức:
\[ a = \frac{\Delta v}{\Delta t} \]
Trong đó:
- \( a \) là gia tốc (m/s²)
- \( \Delta v \) là sự thay đổi vận tốc (m/s)
- \( \Delta t \) là khoảng thời gian thay đổi (s)
Nếu \( a = 0 \), điều đó có nghĩa là vật đang chuyển động thẳng đều (vận tốc không đổi).
Gia tốc trong Chuyển động Thẳng Đều
Trong chuyển động thẳng đều, vận tốc của vật là không đổi, tức là gia tốc bằng 0. Điều này có nghĩa là không có sự thay đổi nào về vận tốc theo thời gian. Nếu một vật đang chuyển động với vận tốc 3 m/s trong một khoảng thời gian dài mà không có lực nào tác dụng thêm, vật sẽ tiếp tục chuyển động với vận tốc đó.
Tính Toán Vận Tốc Và Gia Tốc Từ Các Bài Tập Thực Tế
Ví dụ, nếu một vật đang chuyển động với vận tốc 3 m/s trên một mặt phẳng không ma sát, và lực tác dụng lên nó đột ngột mất đi, vật sẽ tiếp tục chuyển động với vận tốc 3 m/s. Điều này phù hợp với định luật I Newton, tức là vật sẽ duy trì trạng thái chuyển động thẳng đều nếu không có lực tác dụng làm thay đổi trạng thái của nó.
Hãy xem xét một bài toán khác: Nếu một vật đang chuyển động với vận tốc ban đầu \( v_0 \), và lực tác dụng làm tăng tốc độ của nó lên \( v_1 \) sau một khoảng thời gian \( t \), gia tốc có thể được tính như sau:
\[ a = \frac{v_1 - v_0}{t} \]
Như vậy, sự thay đổi vận tốc theo thời gian chính là gia tốc của vật.
Kết luận
Việc nắm vững khái niệm về vận tốc và gia tốc sẽ giúp hiểu rõ hơn về các hiện tượng chuyển động trong thực tế, cũng như giúp giải quyết các bài toán liên quan đến chuyển động một cách hiệu quả.

Tài Liệu Tham Khảo Và Nguồn Học Tập
Việc học và nghiên cứu về chuyển động thẳng đều, vận tốc và gia tốc đòi hỏi sự hiểu biết vững chắc về lý thuyết cũng như khả năng áp dụng vào các bài toán thực tế. Dưới đây là một số tài liệu và nguồn học tập hữu ích để bạn có thể tham khảo và nâng cao kiến thức của mình.
Sách Giáo Khoa Vật Lý Lớp 10
Sách giáo khoa Vật Lý lớp 10 là tài liệu cơ bản và chính thống nhất, cung cấp các kiến thức nền tảng về chuyển động thẳng đều, bao gồm định luật Newton, các công thức tính toán vận tốc và gia tốc. Các bài tập trong sách sẽ giúp bạn rèn luyện khả năng áp dụng lý thuyết vào thực tế.
Tài Liệu Ôn Tập Và Bài Giảng Trực Tuyến
Các trang web giáo dục như Olm.vn và Hoc24.vn cung cấp các bài giảng video, bài tập và câu hỏi trắc nghiệm liên quan đến chuyển động thẳng đều. Bạn có thể dễ dàng truy cập và luyện tập tại nhà.
- Olm.vn: Nền tảng cung cấp bài giảng và bài tập trực tuyến với các chủ đề vật lý đa dạng, bao gồm chuyển động thẳng đều.
- Hoc24.vn: Cung cấp nhiều bài giảng, tài liệu ôn tập và các bài kiểm tra giúp củng cố kiến thức về chuyển động và lực.
Ứng Dụng Của Kiến Thức Vật Lý Trong Các Lĩnh Vực Khác Nhau
Hiểu rõ về vận tốc và gia tốc không chỉ giúp bạn trong học tập mà còn có thể áp dụng vào thực tế. Chẳng hạn, trong ngành giao thông vận tải, kiến thức này giúp thiết kế các phương tiện di chuyển an toàn và hiệu quả hơn. Trong thể thao, nó hỗ trợ việc phân tích kỹ thuật chuyển động của vận động viên để cải thiện thành tích.
Các Diễn Đàn Học Tập Và Thảo Luận
Tham gia các diễn đàn như Diendan.hocmai.vn hoặc Vatlysupham.com là một cách tuyệt vời để trao đổi kiến thức với những người học khác. Tại đây, bạn có thể đặt câu hỏi, chia sẻ kinh nghiệm học tập và tìm kiếm lời giải cho các bài toán khó.
- Diendan.hocmai.vn: Diễn đàn hỗ trợ học sinh trao đổi kiến thức và giải đáp thắc mắc về các bài tập vật lý.
- Vatlysupham.com: Cộng đồng giáo viên và học sinh với nhiều tài liệu và thảo luận hữu ích về vật lý.
Kết Luận
Việc sử dụng đa dạng các nguồn tài liệu tham khảo và công cụ học tập sẽ giúp bạn hiểu sâu hơn về các khái niệm liên quan đến chuyển động thẳng đều, vận tốc và gia tốc. Hãy tận dụng các tài nguyên này để nâng cao kiến thức và ứng dụng chúng vào thực tế.