Chủ đề chuyển động brown: Chuyển động Brown là hiện tượng chuyển động ngẫu nhiên của các hạt nhỏ trong môi trường chất lỏng hoặc khí, được phát hiện bởi nhà thực vật học Robert Brown vào năm 1827. Không chỉ là một khái niệm quan trọng trong vật lý và hóa học, chuyển động Brown còn có ứng dụng rộng rãi trong các lĩnh vực như kinh tế học, đặc biệt là trong việc dự báo giá cổ phiếu trên thị trường chứng khoán, giúp hiểu rõ hơn về các hiện tượng tài chính phức tạp.
Mục lục
- Chuyển động Brown: Khái niệm và Ứng dụng
- Giới thiệu về Chuyển động Brown
- Nguyên lý và Toán học của Chuyển động Brown
- Ứng dụng của Chuyển động Brown
- Thí nghiệm và Mô phỏng Chuyển động Brown
- Chuyển động Brown và các lý thuyết liên quan
- Tầm quan trọng của Chuyển động Brown trong nghiên cứu khoa học
- Những thách thức và giới hạn của nghiên cứu về Chuyển động Brown
Chuyển động Brown: Khái niệm và Ứng dụng
Chuyển động Brown là một hiện tượng quan sát được khi các hạt nhỏ lơ lửng trong chất lỏng hoặc khí di chuyển một cách ngẫu nhiên. Được đặt theo tên của nhà thực vật học Robert Brown, người đã quan sát hiện tượng này lần đầu tiên vào năm 1827, chuyển động này là kết quả của các va chạm không đồng đều giữa các hạt nhỏ với các phân tử chất lỏng hoặc khí xung quanh chúng.
1. Đặc điểm của Chuyển động Brown
- Chuyển động Brown xảy ra liên tục và không có quy luật rõ ràng.
- Hiện tượng này có thể được mô tả bằng các phương trình vi phân ngẫu nhiên, đặc biệt là phương trình Langevin.
- Các hạt càng nhỏ, chuyển động Brown càng rõ ràng.
2. Ứng dụng trong Khoa học và Công nghệ
Chuyển động Brown đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và công nghệ:
- Vật lý: Chuyển động Brown là một minh chứng thực nghiệm cho sự tồn tại của các phân tử và nguyên tử, hỗ trợ phát triển thuyết động học phân tử.
- Hóa học: Hiện tượng này giúp hiểu rõ hơn về các quá trình khuếch tán, nơi mà các chất hòa tan di chuyển từ vùng có nồng độ cao đến vùng có nồng độ thấp.
- Sinh học: Trong sinh học tế bào, chuyển động Brown giải thích cách thức các phân tử và ion di chuyển trong môi trường tế bào.
- Tài chính: Mô hình chuyển động Brown được ứng dụng trong lý thuyết thị trường tài chính để mô tả biến động giá cổ phiếu và các tài sản tài chính khác.
3. Mô hình Toán học của Chuyển động Brown
Chuyển động Brown được mô hình hóa bằng một quá trình ngẫu nhiên liên tục có giá trị thực \( W(t) \) với các đặc điểm:
- \( W(0) = 0 \): Quá trình bắt đầu từ gốc tọa độ.
- \( W(t) - W(s) \sim \mathcal{N}(0, t-s) \): Các gia số của quá trình tuân theo phân phối chuẩn với giá trị trung bình 0 và phương sai tỷ lệ với \( t-s \).
- Quá trình \( W(t) \) có các gia số độc lập: Nếu \( 0 \leq s_1 \leq t_1 \leq s_2 \leq t_2 \), thì \( W(t_1) - W(s_1) \) và \( W(t_2) - W(s_2) \) là các biến ngẫu nhiên độc lập.
4. Ứng dụng trong Dự báo Giá Cổ phiếu
Chuyển động Brown được sử dụng trong các mô hình tài chính để dự báo biến động giá cổ phiếu. Các mô hình này giả định rằng giá cổ phiếu biến đổi theo một quá trình tương tự như chuyển động Brown, từ đó có thể ước lượng rủi ro và lợi nhuận trong đầu tư.
Một ví dụ điển hình là việc sử dụng chuyển động Brown để mô tả các dao động của chỉ số chứng khoán. Nhờ đó, các nhà kinh tế học và nhà đầu tư có thể phân tích và dự báo xu hướng thị trường.
Kết luận
Chuyển động Brown không chỉ là một khái niệm quan trọng trong vật lý và hóa học mà còn có ứng dụng rộng rãi trong sinh học và tài chính. Khả năng mô tả các quá trình ngẫu nhiên một cách chính xác giúp chuyển động Brown trở thành một công cụ hữu ích trong nghiên cứu khoa học và ứng dụng thực tế.
.png)
Giới thiệu về Chuyển động Brown
Chuyển động Brown là hiện tượng các hạt nhỏ, chẳng hạn như hạt phấn hoặc bụi, chuyển động ngẫu nhiên khi được đặt trong chất lỏng hoặc chất khí. Hiện tượng này lần đầu tiên được nhà thực vật học người Scotland, Robert Brown, quan sát vào năm 1827 khi ông theo dõi chuyển động của các hạt phấn hoa dưới kính hiển vi. Ông nhận thấy các hạt này chuyển động không ngừng và không theo một hướng cụ thể nào.
Chuyển động này được gây ra bởi các va chạm liên tục và ngẫu nhiên của các phân tử chất lỏng hoặc khí với các hạt nhỏ. Các phân tử này chuyển động nhanh chóng và không ngừng, đẩy các hạt theo mọi hướng, dẫn đến chuyển động ngẫu nhiên mà chúng ta quan sát được.
- Chuyển động Brown được xem như một ví dụ của quá trình ngẫu nhiên, đóng vai trò quan trọng trong việc chứng minh sự tồn tại của các phân tử và nguyên tử.
- Mô hình toán học cho chuyển động Brown được mô tả bởi quá trình Wiener, một quá trình ngẫu nhiên liên tục với phân phối chuẩn, được phát triển bởi nhà toán học Norbert Wiener.
- Hiện tượng này có ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý, hóa học, sinh học, và tài chính, giúp hiểu rõ hơn về các hệ thống phức tạp và dự đoán sự biến đổi ngẫu nhiên.
Công trình nghiên cứu của Albert Einstein vào đầu thế kỷ 20 đã giải thích lý thuyết cơ bản về chuyển động Brown, góp phần vào sự phát triển của lý thuyết nguyên tử và cũng đóng góp cho sự phát triển của thống kê và xác suất trong khoa học hiện đại.
Nguyên lý và Toán học của Chuyển động Brown
Chuyển động Brown là một hiện tượng vật lý mô tả chuyển động ngẫu nhiên của các hạt nhỏ lơ lửng trong chất lỏng hoặc khí. Hiện tượng này lần đầu tiên được quan sát bởi nhà thực vật học người Anh, Robert Brown, vào năm 1827 khi ông quan sát chuyển động của các hạt phấn hoa trong nước qua kính hiển vi.
Nguyên lý cơ bản của chuyển động Brown là do các va chạm ngẫu nhiên giữa các hạt nhỏ và các phân tử của môi trường xung quanh. Sự va chạm này gây ra sự di chuyển không ngừng và không theo hướng nhất định của các hạt, dẫn đến chuyển động zigzag không có quy tắc. Mức độ chuyển động phụ thuộc vào nhiệt độ của môi trường: nhiệt độ càng cao, chuyển động của các hạt càng mạnh.
Toán học mô tả chuyển động Brown thường sử dụng các mô hình xác suất và quá trình ngẫu nhiên. Một trong những mô hình toán học nổi tiếng nhất mô tả hiện tượng này là quá trình Wiener. Quá trình Wiener là một quá trình Markov liên tục, trong đó giá trị của nó thay đổi ngẫu nhiên theo thời gian, với sự thay đổi này tuân theo phân phối chuẩn.
- Phương trình cơ bản cho chuyển động Brown có thể được biểu diễn như sau:
Trong đó:
- \(x(t)\): vị trí của hạt tại thời điểm \(t\).
- \(\Delta x\): sự thay đổi vị trí do tác động ngẫu nhiên trong khoảng thời gian \(\Delta t\).
Chuyển động Brown có ứng dụng rộng rãi trong nhiều lĩnh vực, từ vật lý, hóa học cho đến sinh học và tài chính. Trong thị trường chứng khoán, mô hình chuyển động Brown được sử dụng để mô tả giá cổ phiếu và các tài sản tài chính khác theo thời gian, giúp các nhà phân tích dự đoán xu hướng biến động của thị trường.

Ứng dụng của Chuyển động Brown
Chuyển động Brown có rất nhiều ứng dụng trong các lĩnh vực khác nhau của khoa học và công nghệ. Một trong những ứng dụng phổ biến nhất là trong lĩnh vực tài chính, đặc biệt là dự báo và mô phỏng giá cổ phiếu trên thị trường chứng khoán. Mô hình chuyển động Brown giúp mô tả sự biến động ngẫu nhiên của giá cả, từ đó giúp các nhà đầu tư đưa ra quyết định chính xác hơn.
- Trong tài chính, chuyển động Brown được sử dụng để xây dựng các mô hình dự báo giá cổ phiếu và phân tích rủi ro. Những mô hình này giúp dự đoán sự thay đổi giá cả và đo lường biến động của thị trường.
- Trong vật lý và hóa học, chuyển động Brown giúp giải thích các hiện tượng liên quan đến sự khuếch tán của các hạt nhỏ trong chất lỏng hoặc khí. Đây là cơ sở quan trọng để phát triển các phương pháp đo lường kích thước hạt và tốc độ khuếch tán.
- Chuyển động Brown cũng được áp dụng trong sinh học để nghiên cứu các quá trình sinh học ngẫu nhiên, như sự di chuyển của phân tử trong tế bào và sự tương tác của các phân tử sinh học.
- Trong kỹ thuật, các mô hình chuyển động Brown được sử dụng để phân tích độ tin cậy của hệ thống và dự đoán thời gian hỏng hóc của các thiết bị.
Các ứng dụng của chuyển động Brown không chỉ dừng lại ở lý thuyết mà còn có tác động thực tiễn quan trọng trong việc phân tích dữ liệu và dự báo trong nhiều ngành công nghiệp khác nhau. Điều này làm cho chuyển động Brown trở thành một công cụ mạnh mẽ và không thể thiếu trong nghiên cứu khoa học hiện đại.

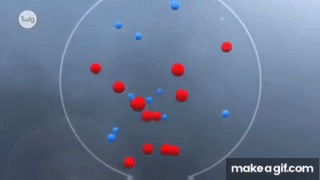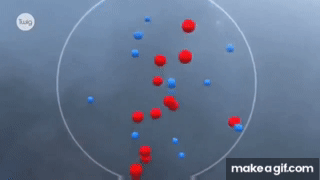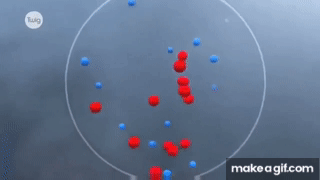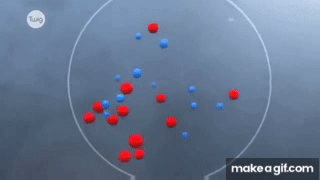
Thí nghiệm và Mô phỏng Chuyển động Brown
Chuyển động Brown là hiện tượng các hạt nhỏ như hạt phấn hoa, khi được thả vào chất lỏng, di chuyển không ngừng dưới tác động của các phân tử môi trường. Để quan sát hiện tượng này, chúng ta có thể thực hiện một số thí nghiệm cơ bản.
Một trong những thí nghiệm phổ biến để quan sát chuyển động Brown là sử dụng kính hiển vi để theo dõi các hạt nhỏ trong nước:
- Đầu tiên, đặt một giọt nước có chứa các hạt nhỏ (như phấn hoa) lên một lam kính.
- Sau đó, dùng kính hiển vi quan sát. Bạn sẽ thấy các hạt này chuyển động ngẫu nhiên và không ngừng.
Để hiểu rõ hơn về chuyển động Brown, chúng ta có thể sử dụng mô phỏng máy tính:
- Các phần mềm mô phỏng như Matlab hoặc Python có thể tạo ra các mô hình chuyển động Brown. Điều này cho phép chúng ta quan sát và phân tích chuyển động của các hạt trong môi trường ảo.
- Mô phỏng giúp minh họa rõ ràng cách mà các phân tử va chạm với hạt lớn hơn, làm cho chúng di chuyển một cách ngẫu nhiên.
Một ứng dụng cụ thể của mô phỏng chuyển động Brown là trong nghiên cứu các hiện tượng nhiệt động lực học và vật lý hạt nhân. Bằng cách mô phỏng chuyển động của các hạt, các nhà khoa học có thể dự đoán và kiểm chứng các lý thuyết về sự phân bố và tương tác của hạt trong các môi trường khác nhau.

Chuyển động Brown và các lý thuyết liên quan
Chuyển động Brown là chuyển động ngẫu nhiên của các hạt rất nhỏ, có thể nhìn thấy dưới kính hiển vi, khi chúng bị các phân tử của chất lỏng hoặc khí xung quanh tác động. Hiện tượng này lần đầu tiên được quan sát bởi nhà thực vật học người Anh, Robert Brown, vào năm 1827 khi ông nghiên cứu các hạt phấn hoa trong nước.
Để hiểu rõ hơn về chuyển động Brown, các nhà khoa học đã phát triển nhiều lý thuyết và mô hình toán học. Một trong những lý thuyết nổi tiếng nhất được đưa ra bởi Albert Einstein vào năm 1905. Ông đã chỉ ra rằng chuyển động Brown có thể được giải thích thông qua động học phân tử, khi các phân tử nước chuyển động hỗn loạn và va chạm vào các hạt nhỏ, tạo nên chuyển động không ngừng của chúng. Điều này giúp khẳng định sự tồn tại của nguyên tử và phân tử, đồng thời xác nhận tính đúng đắn của thuyết động học phân tử.
- Nguyên lý động học phân tử: Chuyển động Brown minh họa cho nguyên lý rằng các phân tử của chất khí hay chất lỏng luôn chuyển động và va chạm liên tục. Sự va chạm này là nguyên nhân chính gây ra chuyển động không ngừng của các hạt nhỏ.
- Liên hệ với nhiệt động học: Chuyển động Brown cũng liên quan đến nhiệt độ. Khi nhiệt độ tăng, năng lượng của các phân tử xung quanh cũng tăng, khiến cho các hạt nhỏ trong chất lỏng hay khí chuyển động nhanh hơn. Điều này giải thích tại sao hiện tượng khuếch tán xảy ra nhanh hơn ở nhiệt độ cao.
- Mô hình toán học: Chuyển động Brown được mô hình hóa thông qua phương trình Langevin và mô hình chuyển động ngẫu nhiên. Các phương trình này cho phép dự đoán vị trí và tốc độ của các hạt nhỏ theo thời gian, dựa trên các lực tác động từ môi trường xung quanh.
Như vậy, chuyển động Brown không chỉ là một hiện tượng vật lý thú vị mà còn cung cấp những bằng chứng quan trọng hỗ trợ cho sự phát triển của các lý thuyết khoa học cơ bản, đặc biệt trong lĩnh vực hóa học và vật lý hiện đại.
XEM THÊM:
Tầm quan trọng của Chuyển động Brown trong nghiên cứu khoa học
Chuyển động Brown đóng vai trò quan trọng trong việc xác nhận sự tồn tại của các nguyên tử và phân tử, là nền tảng cho lý thuyết nguyên tử hiện đại. Những mô hình toán học liên quan đến chuyển động này không chỉ giúp giải thích các hiện tượng vật lý và hóa học mà còn mở ra nhiều ứng dụng trong các lĩnh vực khác như sinh học, tài chính và kỹ thuật.
- Kiểm chứng sự tồn tại của nguyên tử: Những thí nghiệm và quan sát về chuyển động Brown đã giúp chứng minh sự tồn tại của các nguyên tử, một khái niệm mà trước đây chỉ là lý thuyết.
- Ứng dụng trong tài chính: Mô hình toán học của chuyển động Brown được sử dụng để mô phỏng và dự báo các biến động giá cổ phiếu và tài sản tài chính khác.
- Ứng dụng trong sinh học: Trong lĩnh vực sinh học, chuyển động Brown giúp giải thích sự phân tán của các hạt và sự khuếch tán của chất trong tế bào, đóng vai trò quan trọng trong các nghiên cứu y học và sinh học phân tử.
- Ứng dụng trong hóa học: Mô hình này còn được sử dụng để dự đoán phản ứng hóa học và tốc độ phản ứng, hỗ trợ phát triển các quá trình công nghệ hóa học hiệu quả hơn.
Nhờ vào việc mô hình hóa và hiểu rõ chuyển động Brown, các nhà khoa học có thể phát triển các lý thuyết và ứng dụng mới, không chỉ giới hạn trong phòng thí nghiệm mà còn có tác động thực tiễn đến đời sống và công nghiệp.

Những thách thức và giới hạn của nghiên cứu về Chuyển động Brown
Chuyển động Brown đã đóng góp rất lớn cho khoa học, nhưng việc nghiên cứu về nó cũng gặp phải nhiều thách thức và giới hạn đáng kể. Dưới đây là những khó khăn chính mà các nhà nghiên cứu thường gặp phải:
1. Khó khăn trong quan sát thực nghiệm
Việc quan sát chuyển động Brown trong môi trường thực tế không hề dễ dàng. Kích thước nhỏ bé của các hạt và sự nhiễu loạn từ các yếu tố ngoại cảnh làm cho việc theo dõi chính xác chuyển động của các hạt trở nên phức tạp. Các thiết bị đo đạc đòi hỏi phải có độ nhạy cao và thường phải hoạt động trong môi trường được kiểm soát chặt chẽ.
2. Giới hạn của mô phỏng máy tính
Dù đã có sự phát triển vượt bậc trong công nghệ mô phỏng máy tính, nhưng việc tái tạo chính xác chuyển động Brown vẫn gặp nhiều thách thức. Các mô hình toán học thường dựa trên các giả định đơn giản hóa, điều này có thể dẫn đến sai số trong việc dự đoán hành vi thực tế của các hạt. Hơn nữa, việc mô phỏng đòi hỏi một lượng lớn tài nguyên tính toán, điều này giới hạn khả năng của các nghiên cứu quy mô lớn.
3. Ứng dụng trong môi trường thực tế
Mặc dù chuyển động Brown có ứng dụng rộng rãi trong nhiều lĩnh vực, nhưng việc ứng dụng lý thuyết này vào các bài toán thực tế vẫn còn nhiều hạn chế. Các mô hình dựa trên chuyển động Brown thường chỉ áp dụng hiệu quả trong những điều kiện lý tưởng, trong khi các yếu tố như nhiệt độ, áp suất và nhiễu loạn môi trường có thể làm giảm độ chính xác của các dự đoán.
Những thách thức này không chỉ đặt ra yêu cầu về việc phát triển các phương pháp quan sát và mô phỏng tiên tiến hơn, mà còn thúc đẩy sự hiểu biết sâu sắc hơn về các yếu tố tác động đến chuyển động Brown trong môi trường thực tế.