Chủ đề chuyển động song phẳng: Chuyển động song phẳng là một khái niệm cơ bản trong cơ học, giúp giải thích các hiện tượng chuyển động của vật rắn trong một mặt phẳng. Bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện về chuyển động song phẳng, từ khái niệm, phân loại đến các ứng dụng thực tiễn trong đời sống và kỹ thuật.
Mục lục
Chuyển động song phẳng
Chuyển động song phẳng là một khái niệm cơ bản trong cơ học, thuộc phần động học vật rắn. Đây là loại chuyển động mà tất cả các điểm của một vật rắn đều di chuyển theo các đường thẳng song song với nhau và nằm trong cùng một mặt phẳng. Khái niệm này được ứng dụng rộng rãi trong các bài toán cơ học và là nền tảng để hiểu về chuyển động phức tạp hơn của các hệ vật rắn.
Phân loại chuyển động song phẳng
- Chuyển động tịnh tiến: Khi mọi điểm trên vật rắn đều chuyển động theo những quỹ đạo giống nhau và cùng vận tốc.
- Chuyển động quay quanh một trục: Khi mọi điểm trên vật rắn quay quanh một trục cố định trong không gian và nằm trong cùng một mặt phẳng.
- Chuyển động hỗn hợp: Là sự kết hợp giữa chuyển động tịnh tiến và chuyển động quay.
Phương trình chuyển động song phẳng
Để mô tả chuyển động song phẳng của một vật rắn, người ta sử dụng các phương trình sau:
- Phương trình vận tốc: Vận tốc tại bất kỳ điểm nào trên vật rắn có thể được xác định bằng công thức:
- Phương trình gia tốc: Gia tốc tại bất kỳ điểm nào trên vật rắn được xác định bằng:
\[\vec{v} = \vec{v_O} + \vec{\omega} \times \vec{r}\]
\[\vec{a} = \vec{a_O} + \vec{\alpha} \times \vec{r} + \vec{\omega} \times (\vec{\omega} \times \vec{r})\]
Ứng dụng của chuyển động song phẳng
Chuyển động song phẳng có nhiều ứng dụng thực tiễn trong các ngành công nghiệp và kỹ thuật, chẳng hạn như trong thiết kế máy móc, xe cộ, và các hệ thống cơ học phức tạp. Việc hiểu rõ và mô tả chính xác chuyển động này giúp các kỹ sư và nhà khoa học tính toán và tối ưu hóa hoạt động của các thiết bị và hệ thống.
Ví dụ minh họa
Một ví dụ điển hình của chuyển động song phẳng là bánh xe của một chiếc xe khi di chuyển trên mặt đường thẳng. Các điểm trên bánh xe đều nằm trên những mặt phẳng song song và chuyển động theo các đường thẳng song song, làm cho bánh xe quay trơn tru mà không bị lệch.
Kết luận
Chuyển động song phẳng là một phần quan trọng trong cơ học và động học vật rắn, giúp chúng ta hiểu rõ hơn về cách các vật thể di chuyển và tương tác trong không gian. Kiến thức này không chỉ có ý nghĩa học thuật mà còn có ứng dụng rộng rãi trong cuộc sống và công nghiệp.

.png)
1. Giới thiệu về chuyển động song phẳng
Chuyển động song phẳng là một khái niệm quan trọng trong cơ học, mô tả sự di chuyển của vật rắn trong một mặt phẳng cố định. Trong loại chuyển động này, tất cả các điểm trên vật rắn đều di chuyển theo các đường thẳng song song với nhau, giúp việc phân tích và tính toán trở nên đơn giản hơn.
Một cách dễ hiểu, chuyển động song phẳng có thể bao gồm các dạng chuyển động như chuyển động tịnh tiến, nơi mọi điểm trên vật rắn di chuyển cùng một khoảng cách và hướng, hoặc chuyển động quay quanh một trục cố định nằm trong mặt phẳng đó.
Trong toán học, để mô tả chính xác chuyển động này, chúng ta thường sử dụng các phương trình vector và đại số tuyến tính. Chẳng hạn, nếu một điểm O trên vật rắn có vị trí \(\vec{r_O}\) và vận tốc \(\vec{v_O}\), thì vận tốc của một điểm bất kỳ M trên vật rắn có thể được tính bằng công thức:
\[
\vec{v_M} = \vec{v_O} + \vec{\omega} \times \vec{r_{M/O}}
\]
Trong đó, \(\vec{\omega}\) là vector vận tốc góc và \(\vec{r_{M/O}}\) là vector vị trí của điểm M so với điểm O.
Chuyển động song phẳng đóng vai trò quan trọng trong việc thiết kế và phân tích các cơ cấu máy móc, đặc biệt là trong ngành cơ khí và kỹ thuật, nơi các bộ phận cần được đảm bảo di chuyển theo những quỹ đạo chính xác và ổn định.
2. Phân loại chuyển động song phẳng
Chuyển động song phẳng có thể được phân loại dựa trên hình thức di chuyển của vật rắn. Các dạng chính của chuyển động song phẳng bao gồm:
- Chuyển động tịnh tiến: Trong chuyển động tịnh tiến, mọi điểm trên vật rắn di chuyển cùng một khoảng cách theo một hướng xác định. Ví dụ, khi một vật rắn di chuyển trên một mặt phẳng mà không xoay hoặc thay đổi hình dạng, đó là chuyển động tịnh tiến. Tốc độ của các điểm trên vật rắn là giống nhau, và không có sự xuất hiện của vận tốc góc.
- Chuyển động quay: Đây là loại chuyển động mà mọi điểm trên vật rắn di chuyển quanh một trục cố định nằm trong mặt phẳng đó. Trong trường hợp này, các điểm trên vật rắn sẽ mô tả các quỹ đạo tròn, và tốc độ góc \(\omega\) đóng vai trò quan trọng trong việc xác định chuyển động của vật.
- Chuyển động hỗn hợp: Là sự kết hợp của cả chuyển động tịnh tiến và chuyển động quay. Trong chuyển động hỗn hợp, vật rắn không chỉ di chuyển theo một hướng mà còn quay quanh một trục cố định. Một ví dụ phổ biến là chuyển động của các bánh răng trong một hệ thống cơ khí, nơi mỗi bánh răng vừa quay quanh trục của nó vừa di chuyển tịnh tiến cùng với hệ thống.
Để phân tích các loại chuyển động này, người ta thường sử dụng các công cụ toán học như vector vận tốc, gia tốc và các phương trình động lực học. Đặc biệt, trong chuyển động quay, vector vận tốc góc \(\omega\) và gia tốc góc \(\alpha\) là những đại lượng cần thiết để mô tả sự biến đổi của vật rắn.

3. Các phương trình cơ bản
Trong chuyển động song phẳng, các phương trình cơ bản thường được sử dụng để mô tả chuyển động của một vật rắn trong mặt phẳng. Dưới đây là các phương trình chính:
- Phương trình vị trí: Phương trình này mô tả vị trí của một điểm bất kỳ trên vật rắn trong mặt phẳng tại một thời điểm bất kỳ. Vị trí thường được biểu diễn bằng vector vị trí \(\mathbf{r}(t)\), trong đó \(t\) là thời gian.
- Phương trình vận tốc: Vận tốc của một điểm trên vật rắn được định nghĩa là đạo hàm của vector vị trí theo thời gian, biểu diễn bởi công thức: \[ \mathbf{v}(t) = \frac{d\mathbf{r}(t)}{dt} \] Trong đó, \(\mathbf{v}(t)\) là vector vận tốc tại thời điểm \(t\).
- Phương trình gia tốc: Gia tốc của một điểm trên vật rắn là đạo hàm của vector vận tốc theo thời gian, được biểu diễn bởi: \[ \mathbf{a}(t) = \frac{d\mathbf{v}(t)}{dt} = \frac{d^2\mathbf{r}(t)}{dt^2} \] Gia tốc này có thể được phân thành hai thành phần: gia tốc tiếp tuyến và gia tốc pháp tuyến.
- Phương trình động lực học: Định luật thứ hai của Newton áp dụng cho chuyển động song phẳng dưới dạng: \[ \mathbf{F} = m \mathbf{a} \] Trong đó, \(\mathbf{F}\) là tổng lực tác dụng lên vật rắn, \(m\) là khối lượng của vật, và \(\mathbf{a}\) là gia tốc của vật.
- Phương trình mômen: Mômen của lực xung quanh một trục xác định được tính bằng: \[ \mathbf{M} = \mathbf{r} \times \mathbf{F} \] Trong đó, \(\mathbf{M}\) là vector mômen, \(\mathbf{r}\) là vector vị trí, và \(\mathbf{F}\) là lực tác dụng.
Các phương trình này là cơ sở để phân tích và giải quyết các bài toán liên quan đến chuyển động song phẳng của vật rắn trong cơ học.
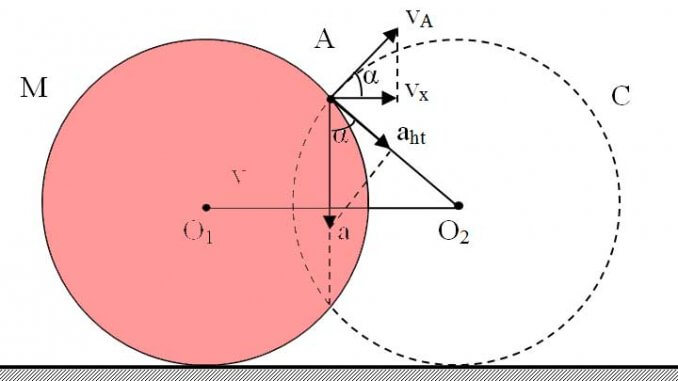
4. Ứng dụng của chuyển động song phẳng trong kỹ thuật
Chuyển động song phẳng có nhiều ứng dụng quan trọng trong kỹ thuật, đặc biệt trong thiết kế và phân tích các hệ thống cơ học. Các ứng dụng này giúp cải thiện hiệu suất và độ chính xác của các máy móc, kết cấu và thiết bị kỹ thuật. Dưới đây là một số ứng dụng phổ biến:
- Thiết kế cơ cấu máy: Chuyển động song phẳng được sử dụng để thiết kế các cơ cấu máy như cơ cấu bốn khâu, cơ cấu cam, và các bộ truyền động, giúp máy móc hoạt động mượt mà và hiệu quả.
- Phân tích kết cấu: Trong xây dựng và cơ khí, chuyển động song phẳng giúp xác định tải trọng, mômen, và ứng suất trong các kết cấu như dầm, cầu và khung nhà, từ đó đảm bảo độ bền và an toàn cho công trình.
- Động lực học của phương tiện: Chuyển động song phẳng là cơ sở để phân tích chuyển động của các phương tiện như ô tô, máy bay, và tàu thuyền. Điều này giúp tối ưu hóa thiết kế và vận hành của các phương tiện, đảm bảo an toàn và hiệu quả.
- Robot và tự động hóa: Trong ngành robot, chuyển động song phẳng được ứng dụng để thiết kế các cánh tay robot, các hệ thống truyền động, và các cơ cấu tự động hóa khác, giúp nâng cao độ chính xác và hiệu suất của robot trong sản xuất và công nghiệp.
- Công nghệ sản xuất: Các quá trình gia công cơ khí như tiện, phay, bào cũng ứng dụng nguyên lý chuyển động song phẳng để đảm bảo chất lượng sản phẩm và tăng cường hiệu suất sản xuất.
Những ứng dụng này cho thấy tầm quan trọng của việc hiểu và áp dụng chuyển động song phẳng trong các lĩnh vực kỹ thuật hiện đại, từ sản xuất công nghiệp đến phát triển công nghệ tiên tiến.

5. Ví dụ thực tế và bài tập vận dụng
Để nắm vững kiến thức về chuyển động song phẳng, việc thực hành thông qua các ví dụ thực tế và bài tập là rất quan trọng. Dưới đây là một số ví dụ minh họa và bài tập giúp bạn áp dụng lý thuyết vào thực tiễn:
Ví dụ thực tế
- Ví dụ 1: Một cần cẩu nâng vật có trọng lượng \(500\) kg theo chuyển động song phẳng. Tính lực căng trong dây cáp và mômen tại các khớp nối khi cần cẩu đang hoạt động.
- Ví dụ 2: Một chiếc ô tô đang di chuyển trên một mặt phẳng nghiêng với vận tốc \(v = 60\) km/h. Phân tích lực tác dụng lên ô tô và xác định quỹ đạo của nó.
Bài tập vận dụng
- Bài tập 1: Một khối gỗ trượt xuống mặt phẳng nghiêng với góc nghiêng \(\theta = 30^\circ\). Hãy xác định gia tốc của khối gỗ khi biết hệ số ma sát trượt giữa khối gỗ và mặt phẳng là \(\mu = 0.2\).
- Bài tập 2: Một vật nặng \(10\) kg được treo vào đầu một sợi dây và thực hiện chuyển động song phẳng trong mặt phẳng đứng. Tính lực căng trong dây tại điểm thấp nhất của chuyển động khi vận tốc của vật tại điểm đó là \(v = 5\) m/s.
- Bài tập 3: Một thanh thép dài \(2\) m quay quanh một trục cố định tại một đầu. Đầu kia của thanh di chuyển theo một quỹ đạo song phẳng. Tính mômen quán tính của thanh thép đối với trục quay.
Các bài tập này giúp củng cố kiến thức về chuyển động song phẳng, giúp bạn hiểu rõ hơn cách áp dụng lý thuyết vào các tình huống thực tế trong kỹ thuật và đời sống.
XEM THÊM:
6. Tổng kết và kết luận
Chuyển động song phẳng là một khái niệm quan trọng trong cơ học, đóng vai trò nền tảng trong việc hiểu rõ các hiện tượng vật lý và ứng dụng trong kỹ thuật. Thông qua các phần trước, chúng ta đã tìm hiểu về khái niệm, phân loại, và các phương trình cơ bản của chuyển động song phẳng. Để kết luận, chúng ta sẽ tóm tắt lại những nội dung chính và nhấn mạnh tầm quan trọng của việc nắm vững kiến thức này.
6.1 Tóm tắt lại các khái niệm và phương trình chính
Chuyển động song phẳng được phân thành ba loại chính: chuyển động tịnh tiến, chuyển động quay quanh trục, và chuyển động hỗn hợp. Mỗi loại chuyển động có các đặc trưng riêng và được mô tả bởi các phương trình vận tốc và gia tốc tương ứng.
- Chuyển động tịnh tiến: Đặc trưng bởi sự di chuyển của vật thể mà tất cả các điểm của vật thể có cùng vận tốc và gia tốc.
- Chuyển động quay quanh trục: Vật thể quay quanh một trục cố định, trong đó các điểm trên vật thể có vận tốc và gia tốc góc.
- Chuyển động hỗn hợp: Kết hợp giữa chuyển động tịnh tiến và chuyển động quay, tạo ra một dạng chuyển động phức tạp hơn.
Các phương trình cơ bản như phương trình vận tốc \(\mathbf{v} = \frac{d\mathbf{r}}{dt}\) và phương trình gia tốc \(\mathbf{a} = \frac{d\mathbf{v}}{dt}\) là những công cụ cần thiết để phân tích và giải quyết các vấn đề liên quan đến chuyển động song phẳng.
6.2 Tầm quan trọng của việc hiểu biết về chuyển động song phẳng
Việc nắm vững kiến thức về chuyển động song phẳng không chỉ giúp hiểu rõ hơn về cơ học lý thuyết mà còn có giá trị thực tiễn cao trong kỹ thuật và công nghiệp. Kiến thức này được áp dụng rộng rãi trong thiết kế và phân tích các hệ thống cơ học, từ máy móc đơn giản đến các hệ thống phức tạp như ô tô, máy bay, và robot.
Đặc biệt, trong ngành công nghiệp ô tô, hiểu biết về chuyển động song phẳng giúp cải thiện thiết kế và tối ưu hóa hoạt động của các thành phần như động cơ, hệ thống treo, và hệ thống lái. Nhờ đó, các phương tiện giao thông trở nên an toàn hơn, hiệu quả hơn, và thân thiện với môi trường hơn.
6.3 Hướng nghiên cứu và phát triển thêm trong tương lai
Trong tương lai, nghiên cứu về chuyển động song phẳng sẽ tiếp tục được mở rộng, đặc biệt là trong các lĩnh vực công nghệ cao như tự động hóa, robot, và kỹ thuật y sinh. Các ứng dụng mới của chuyển động song phẳng sẽ xuất hiện, đòi hỏi các kỹ sư và nhà khoa học không ngừng cập nhật và phát triển kiến thức của mình.
Các nghiên cứu cũng sẽ tập trung vào việc tối ưu hóa các mô hình chuyển động và phát triển các công cụ phân tích mới, giúp giải quyết các bài toán phức tạp hơn, đồng thời mở ra nhiều hướng đi mới cho sự phát triển của khoa học và kỹ thuật.