Chuyển động quay: Khái niệm, ứng dụng và tầm quan trọng trong khoa học

Chuyển động quay là một trong những khái niệm cơ bản trong vật lý học, đặc biệt là khi nghiên cứu về cơ học và động lực học. Dưới đây là các thông tin chi tiết về chủ đề này:

1. Khái niệm chuyển động quay

Chuyển động quay xảy ra khi một vật thể xoay quanh một trục cố định. Trục này có thể là bên trong hoặc bên ngoài vật thể. Một điểm trên vật thể sẽ di chuyển theo một quỹ đạo tròn, và tất cả các điểm trên vật thể đều có tốc độ góc bằng nhau.

2. Tốc độ góc và gia tốc góc

• Tốc độ góc: Được ký hiệu là \(\omega\), tốc độ góc là đại lượng đo lường mức độ nhanh hay chậm của một vật thể quay quanh trục của nó. Công thức tính tốc độ góc là: \[ \omega = \frac{d\theta}{dt} \] trong đó \(d\theta\) là góc quay trong khoảng thời gian \(dt\).
• Gia tốc góc: Được ký hiệu là \(\alpha\), gia tốc góc là đại lượng biểu thị sự thay đổi của tốc độ góc theo thời gian: \[ \alpha = \frac{d\omega}{dt} \]

3. Momen lực và momen quán tính

• Momen lực: Là lực tác động gây ra sự thay đổi trong chuyển động quay của một vật thể. Công thức của momen lực là: \[ \tau = r \times F \] trong đó \(r\) là cánh tay đòn (khoảng cách từ trục quay đến điểm tác dụng lực), và \(F\) là lực tác dụng.
• Momen quán tính: Momen quán tính là đại lượng đặc trưng cho sự khó khăn khi thay đổi trạng thái quay của vật thể. Nó phụ thuộc vào khối lượng của vật và cách khối lượng phân bố quanh trục quay. Công thức tính momen quán tính là: \[ I = \sum m_i r_i^2 \] trong đó \(m_i\) là khối lượng của phần tử vật chất thứ \(i\), và \(r_i\) là khoảng cách từ trục quay đến phần tử đó.

4. Các loại chuyển động quay

Chuyển động quay có thể được phân loại dựa trên tính chất và trục quay:

• Quay đều: Vật thể quay với tốc độ góc không đổi, tức là không có gia tốc góc.
• Quay biến đổi: Tốc độ góc của vật thể thay đổi theo thời gian, có sự xuất hiện của gia tốc góc.
• Quay quanh trục cố định: Trục quay của vật thể là cố định trong không gian.
• Quay quanh trục di động: Trục quay của vật thể cũng chuyển động trong không gian.

5. Ứng dụng của chuyển động quay

Chuyển động quay được ứng dụng rộng rãi trong nhiều lĩnh vực như:

• Trong kỹ thuật: Thiết kế và vận hành các loại máy móc như động cơ, quạt, và các thiết bị cơ khí.
• Trong đời sống hàng ngày: Các thiết bị gia dụng như máy giặt, máy xay sinh tố cũng sử dụng nguyên lý chuyển động quay.
• Trong y học: Sử dụng trong các thiết bị chụp cắt lớp và điều trị bằng bức xạ.

Hiểu rõ về chuyển động quay không chỉ giúp giải quyết các vấn đề trong vật lý học mà còn ứng dụng trong nhiều lĩnh vực thực tiễn khác nhau.

Chuyển động quay là một dạng chuyển động trong đó mọi điểm của một vật thể di chuyển trên quỹ đạo tròn xung quanh một trục cố định hoặc di động. Trong vật lý học, chuyển động quay có ý nghĩa quan trọng trong việc phân tích các hiện tượng cơ học, từ các chuyển động đơn giản đến những hệ thống phức tạp.

• Trục quay: Trục quay là đường thẳng tưởng tượng mà vật thể quay quanh. Trục này có thể cố định (như trong trường hợp bánh xe) hoặc di động (như con quay hồi chuyển).
• Góc quay (\(\theta\)): Góc quay là đại lượng đo lường sự thay đổi vị trí của vật thể quanh trục quay. Đơn vị của góc quay thường là radian (rad) hoặc độ (°).
• Tốc độ góc (\(\omega\)): Tốc độ góc là tốc độ thay đổi của góc quay theo thời gian, được tính bằng công thức: \[ \omega = \frac{d\theta}{dt} \] Trong đó, \(\omega\) có đơn vị là rad/s.
• Gia tốc góc (\(\alpha\)): Gia tốc góc là sự thay đổi của tốc độ góc theo thời gian: \[ \alpha = \frac{d\omega}{dt} \] Đây là đại lượng quan trọng khi nghiên cứu các chuyển động quay biến đổi.

Chuyển động quay có thể được phân loại thành nhiều loại khác nhau dựa trên tính chất của nó, bao gồm chuyển động quay đều, chuyển động quay biến đổi, và chuyển động quanh trục cố định hoặc di động. Mỗi loại chuyển động đều có các đặc trưng và ứng dụng riêng biệt trong cả lý thuyết và thực tiễn.

Trong chuyển động quay, có một số đại lượng vật lý quan trọng giúp mô tả và phân tích các hiện tượng liên quan. Dưới đây là các đại lượng chính:

• 1. Góc quay (\(\theta\)):

  Góc quay là đại lượng biểu thị sự thay đổi vị trí của một điểm trên vật thể khi nó quay quanh trục. Góc quay được đo bằng đơn vị radian (rad) hoặc độ (°). Mối liên hệ giữa góc quay và độ dài cung tròn là:

  \[ \theta = \frac{s}{r} \]

  trong đó \(s\) là độ dài cung tròn và \(r\) là bán kính.

• 2. Tốc độ góc (\(\omega\)):

  Tốc độ góc là đại lượng mô tả mức độ thay đổi của góc quay theo thời gian. Tốc độ góc có đơn vị là radian trên giây (rad/s) và được tính bằng công thức:

  \[ \omega = \frac{d\theta}{dt} \]
• 3. Gia tốc góc (\(\alpha\)):

  Gia tốc góc mô tả sự thay đổi của tốc độ góc theo thời gian. Đây là đại lượng quan trọng trong các chuyển động quay có biến đổi tốc độ. Gia tốc góc được tính bằng công thức:

  \[ \alpha = \frac{d\omega}{dt} \]

  Gia tốc góc có đơn vị là radian trên giây bình phương (rad/s²).

• 4. Momen quán tính (\(I\)):

  Momen quán tính là đại lượng thể hiện sự kháng lại thay đổi trạng thái quay của vật thể. Nó phụ thuộc vào khối lượng của vật và cách mà khối lượng phân bố xung quanh trục quay. Công thức tính momen quán tính cho một vật rắn là:

  \[ I = \sum m_i r_i^2 \]

  trong đó \(m_i\) là khối lượng của phần tử vật chất thứ \(i\) và \(r_i\) là khoảng cách từ phần tử đó đến trục quay. Đơn vị của momen quán tính là kg.m².

• 5. Momen lực (\(\tau\)):

  Momen lực là lực tác động làm cho vật thể quay quanh trục của nó. Momen lực được tính bằng tích của lực (\(F\)) và cánh tay đòn (\(r\)):

  \[ \tau = r \times F \]

  Đơn vị của momen lực là Newton-mét (N.m).

• 6. Động lượng góc (\(L\)):

  Động lượng góc là đại lượng đặc trưng cho chuyển động quay của vật thể. Nó được tính bằng tích của momen quán tính và tốc độ góc:

  \[ L = I \omega \]

  Động lượng góc có đơn vị là kg.m²/s.

• 7. Công và công suất trong chuyển động quay:

  Công trong chuyển động quay được tính bằng tích của momen lực và góc quay:

  \[ W = \tau \theta \]

  Công suất là tốc độ thực hiện công, được tính bằng:

  \[ P = \tau \omega \]

  Đơn vị của công suất là Watt (W).

Phương trình chuyển động quay mô tả mối quan hệ giữa các đại lượng vật lý như góc quay, tốc độ góc, gia tốc góc, và momen lực trong quá trình quay của vật thể. Các phương trình này giúp chúng ta hiểu rõ hơn về cách các yếu tố này ảnh hưởng đến chuyển động của vật thể quay.

• 1. Phương trình động học của chuyển động quay:

  Phương trình động học mô tả mối quan hệ giữa góc quay (\(\theta\)), tốc độ góc (\(\omega\)), gia tốc góc (\(\alpha\)), và thời gian (\(t\)). Chúng tương tự như các phương trình động học của chuyển động tịnh tiến:

  1. Phương trình liên hệ giữa góc quay và tốc độ góc: \[ \theta = \theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2 \]
  2. Phương trình liên hệ giữa tốc độ góc và gia tốc góc: \[ \omega = \omega_0 + \alpha t \]
  3. Phương trình liên hệ giữa tốc độ góc, gia tốc góc và góc quay: \[ \omega^2 = \omega_0^2 + 2\alpha \theta \]

  Trong đó, \(\theta_0\) và \(\omega_0\) lần lượt là góc quay và tốc độ góc ban đầu.

• 2. Phương trình động lực học của chuyển động quay:

  Phương trình động lực học mô tả mối quan hệ giữa momen lực (\(\tau\)), momen quán tính (\(I\)), và gia tốc góc (\(\alpha\)) của vật thể quay. Phương trình cơ bản của động lực học quay là:

  \[ \tau = I \alpha \]

  Phương trình này tương tự như định luật II Newton cho chuyển động tịnh tiến (\(F = ma\)), nhưng áp dụng cho chuyển động quay.

• 3. Phương trình bảo toàn động lượng góc:

  Trong hệ kín không có momen lực ngoài tác động, động lượng góc của hệ được bảo toàn. Phương trình bảo toàn động lượng góc được viết dưới dạng:

  \[ I_1 \omega_1 = I_2 \omega_2 \]

  Trong đó, \(I_1\) và \(I_2\) là momen quán tính của vật thể tại các thời điểm khác nhau, và \(\omega_1\) và \(\omega_2\) là tốc độ góc tương ứng.

Các phương trình trên là công cụ cơ bản và quan trọng để phân tích và giải quyết các bài toán liên quan đến chuyển động quay trong vật lý học và kỹ thuật.

Chuyển động quay có thể được phân loại dựa trên các đặc điểm như tốc độ, trục quay, và tính chất của chuyển động. Dưới đây là các loại chuyển động quay phổ biến trong vật lý học và ứng dụng thực tiễn:

• 1. Chuyển động quay đều:

  Chuyển động quay đều xảy ra khi tốc độ góc của vật thể không thay đổi theo thời gian, nghĩa là gia tốc góc (\(\alpha\)) bằng 0. Trong trường hợp này, mọi điểm trên vật thể đều quay với tốc độ không đổi xung quanh trục quay cố định.

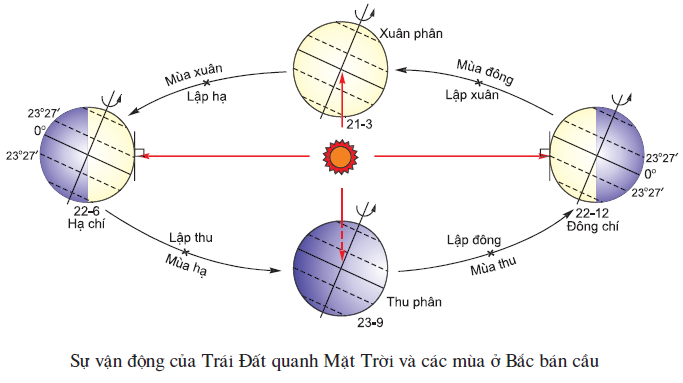
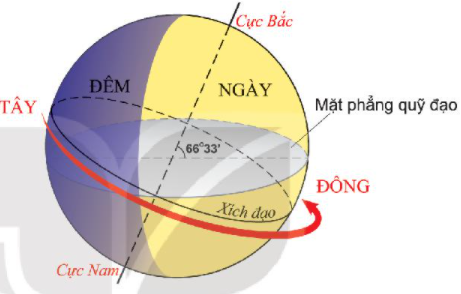
  Ví dụ: Chuyển động quay của Trái Đất quanh trục của nó có thể coi là một chuyển động quay đều.

• 2. Chuyển động quay biến đổi:

  Chuyển động quay biến đổi xảy ra khi tốc độ góc của vật thể thay đổi theo thời gian, tức là có gia tốc góc (\(\alpha \neq 0\)). Chuyển động này có thể là tăng tốc hoặc giảm tốc tùy thuộc vào chiều của gia tốc góc.

  Ví dụ: Quá trình tăng tốc hoặc giảm tốc của một bánh xe khi xe bắt đầu chuyển động hoặc dừng lại.

• 3. Chuyển động quay quanh trục cố định:

  Trong chuyển động này, vật thể quay quanh một trục cố định, và mọi điểm trên vật thể đều nằm trên các quỹ đạo tròn có bán kính không đổi. Trục quay không di chuyển hoặc thay đổi hướng trong quá trình chuyển động.

  Ví dụ: Chuyển động quay của một bánh xe đạp khi di chuyển trên đường thẳng.

• 4. Chuyển động quay quanh trục di động:

  Chuyển động quay quanh trục di động xảy ra khi trục quay của vật thể không cố định mà di chuyển theo thời gian. Loại chuyển động này thường phức tạp hơn và liên quan đến nhiều yếu tố động lực học khác nhau.

  Ví dụ: Chuyển động của một con quay hồi chuyển hoặc sự quay của vệ tinh nhân tạo khi quỹ đạo của nó thay đổi.

• 5. Chuyển động quay kết hợp:

  Chuyển động quay kết hợp là sự kết hợp giữa các loại chuyển động quay khác nhau, chẳng hạn như kết hợp giữa chuyển động quay đều và chuyển động quay biến đổi, hoặc giữa quay quanh trục cố định và trục di động.

  Ví dụ: Sự quay của một quả bóng đá khi nó vừa quay quanh trục của nó vừa di chuyển trên sân.

Hiểu rõ các loại chuyển động quay giúp chúng ta có thể phân tích và ứng dụng chúng trong nhiều lĩnh vực khác nhau, từ kỹ thuật cơ khí đến nghiên cứu vũ trụ.

Chuyển động quay là một hiện tượng cơ bản trong vật lý và có nhiều ứng dụng thực tiễn trong đời sống và công nghiệp. Dưới đây là một số ứng dụng phổ biến của chuyển động quay trong các lĩnh vực khác nhau:

• 1. Ứng dụng trong động cơ và máy móc:

  Chuyển động quay là nguyên lý hoạt động cơ bản của hầu hết các động cơ và máy móc công nghiệp. Ví dụ, động cơ đốt trong của ô tô chuyển đổi chuyển động tịnh tiến của piston thành chuyển động quay của trục khuỷu, qua đó truyền lực để xe di chuyển. Tương tự, các tuabin trong nhà máy điện chuyển đổi năng lượng từ hơi nước, gió hoặc nước thành chuyển động quay để phát điện.

• 2. Ứng dụng trong thiết bị gia dụng:

  Nhiều thiết bị gia dụng sử dụng chuyển động quay để thực hiện các chức năng hàng ngày. Ví dụ, máy giặt sử dụng chuyển động quay của lồng giặt để làm sạch quần áo, máy xay sinh tố sử dụng chuyển động quay của lưỡi dao để xay nhuyễn thực phẩm, và quạt điện sử dụng cánh quạt quay để tạo gió làm mát.

• 3. Ứng dụng trong công nghệ vũ trụ:

  Trong công nghệ vũ trụ, chuyển động quay được sử dụng để ổn định và điều khiển vị trí của vệ tinh và tàu vũ trụ. Ví dụ, các con quay hồi chuyển (gyroscope) trong hệ thống điều khiển quỹ đạo giúp vệ tinh duy trì sự ổn định và hướng chính xác trong không gian.

• 4. Ứng dụng trong y học:

  Chuyển động quay được sử dụng trong nhiều thiết bị y tế. Máy ly tâm là một ví dụ điển hình, nó sử dụng chuyển động quay với tốc độ cao để phân tách các thành phần khác nhau trong máu hoặc mẫu sinh học khác, giúp cho quá trình phân tích và chẩn đoán bệnh trở nên chính xác hơn.

• 5. Ứng dụng trong thể thao và giải trí:

  Chuyển động quay cũng đóng vai trò quan trọng trong thể thao và giải trí. Ví dụ, trong các môn thể thao như trượt ván, nhảy cầu, và thể dục dụng cụ, kỹ thuật quay và kiểm soát chuyển động quay là yếu tố then chốt để thực hiện các động tác phức tạp và đẹp mắt. Ngoài ra, trong giải trí, các trò chơi như vòng quay may mắn, đu quay, và trò chơi xoay tròn đều dựa trên nguyên lý của chuyển động quay.

Như vậy, chuyển động quay không chỉ là một hiện tượng vật lý cơ bản mà còn có những ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của đời sống và công nghiệp, đóng góp vào sự phát triển và tiện nghi của xã hội hiện đại.