Phân Cực Ánh Sáng: Khám Phá Hiện Tượng Quang Học Kỳ Diệu

Phân cực ánh sáng là hiện tượng trong đó các sóng ánh sáng dao động theo một phương nhất định khi truyền qua một môi trường hoặc sau khi bị phản xạ hoặc khúc xạ. Hiện tượng này xuất phát từ bản chất sóng của ánh sáng và có nhiều ứng dụng trong đời sống và công nghệ.

Nguyên Lý Phân Cực Ánh Sáng

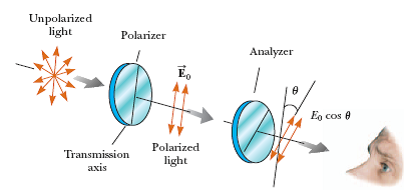
Ánh sáng tự nhiên thường không phân cực, tức là các sóng ánh sáng dao động trong mọi phương vuông góc với phương truyền. Khi ánh sáng đi qua một bộ lọc phân cực hoặc phản xạ dưới một góc đặc biệt (góc Brewster), nó sẽ trở nên phân cực, tức là chỉ dao động theo một phương nhất định.

• Phân Cực Phẳng: Khi ánh sáng chỉ dao động theo một phương duy nhất.
• Phân Cực Tròn: Khi hai phương dao động vuông góc có biên độ bằng nhau và lệch pha 90 độ.
• Phân Cực Elip: Khi hai phương dao động vuông góc có biên độ khác nhau hoặc lệch pha không phải 90 độ.

Công Thức Định Luật Malus

Định luật Malus mô tả sự thay đổi cường độ ánh sáng khi đi qua hai bộ lọc phân cực:

\[
I = I_0 \cos^2(\theta)
\]

Trong đó:

• \(I\) là cường độ ánh sáng sau khi qua bộ lọc phân cực thứ hai.
• \(I_0\) là cường độ ánh sáng ban đầu trước khi qua bộ lọc.
• \(\theta\) là góc giữa trục của hai bộ lọc phân cực.

Ứng Dụng Của Phân Cực Ánh Sáng

• Kính Mát Phân Cực: Giảm độ chói khi nhìn vào bề mặt phản chiếu như nước hoặc đường nhựa.
• Công Nghệ Màn Hình: Màn hình LCD sử dụng ánh sáng phân cực để hiển thị hình ảnh.
• Kiểm Tra Chất Lượng Vật Liệu: Sử dụng ánh sáng phân cực để phát hiện ứng suất trong kính hoặc nhựa.

Hiện Tượng Liên Quan

Hiện tượng phân cực ánh sáng thường được nghiên cứu cùng với các hiện tượng quang học khác như nhiễu xạ và tán xạ ánh sáng. Các thí nghiệm với phân cực ánh sáng có thể giúp chúng ta hiểu rõ hơn về tính chất của ánh sáng và ứng dụng chúng trong khoa học và công nghệ.

Phân cực ánh sáng không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tế, từ kính mát chống chói đến công nghệ màn hình hiện đại.

Phân cực ánh sáng là một khái niệm quan trọng trong quang học, được sử dụng rộng rãi trong nhiều lĩnh vực từ nghiên cứu khoa học đến các ứng dụng công nghệ thực tiễn. Dưới đây là một mục lục chi tiết giúp bạn hiểu rõ hơn về các khía cạnh của phân cực ánh sáng.

1. Khái Niệm và Nguyên Lý Phân Cực Ánh Sáng

• 1.1. Phân Cực Ánh Sáng Là Gì?

• 1.2. Các Loại Phân Cực Ánh Sáng

  • Phân cực phẳng
  • Phân cực tròn
  • Phân cực elip

• 1.3. Nguyên Lý Hoạt Động Của Phân Cực Ánh Sáng

  • Bộ lọc phân cực
  • Góc Brewster
  • Hiện tượng tán xạ Rayleigh

2. Ứng Dụng Của Phân Cực Ánh Sáng

• 2.1. Ứng Dụng Trong Kính Mát Phân Cực

• 2.2. Phân Cực Ánh Sáng Trong Công Nghệ Màn Hình LCD

• 2.3. Ứng Dụng Trong Nhiếp Ảnh

• 2.4. Kiểm Tra Ứng Suất Vật Liệu

3. Các Hiện Tượng Liên Quan Đến Phân Cực Ánh Sáng

• 3.1. Hiện Tượng Nhiễu Xạ

• 3.2. Hiện Tượng Tán Sắc Ánh Sáng

• 3.3. Lăng Kính Phân Cực

4. Định Luật Malus

• 4.1. Công Thức Định Luật Malus

• 4.2. Ví Dụ Minh Họa

5. Lịch Sử Nghiên Cứu Phân Cực Ánh Sáng

• 5.1. Những Phát Hiện Ban Đầu

• 5.2. Các Nhà Khoa Học Nổi Bật Trong Lĩnh Vực Phân Cực Ánh Sáng

6. Các Dạng Bài Tập Về Phân Cực Ánh Sáng

• 6.1. Tính Cường Độ Ánh Sáng Qua Hai Bộ Lọc Phân Cực

• 6.2. Xác Định Góc Brewster Cho Các Vật Liệu Khác Nhau

• 6.3. Tính Toán Phân Cực Trong Các Môi Trường Khác Nhau

• 6.4. Phân Tích Ánh Sáng Phân Cực Qua Lăng Kính

• 6.5. Ứng Dụng Định Luật Malus Để Xác Định Cường Độ Ánh Sáng

• 6.6. Ứng Dụng Phân Cực Trong Quang Học Nhiếp Ảnh

• 6.7. Phân Cực Ánh Sáng Trong Công Nghệ LCD

• 6.8. Xác Định Phân Cực Ánh Sáng Từ Mặt Nước

• 6.9. Phân Tích Hiện Tượng Phân Cực Trong Kính Mát

• 6.10. Tính Toán Cường Độ Ánh Sáng Qua Lớp Phủ Phân Cực

Phân cực ánh sáng là hiện tượng trong đó các dao động của sóng ánh sáng bị giới hạn trong một mặt phẳng cụ thể khi sóng truyền qua không gian. Trong ánh sáng tự nhiên, các dao động diễn ra theo mọi phương vuông góc với phương truyền. Tuy nhiên, khi ánh sáng bị phân cực, chỉ một hướng dao động duy nhất được giữ lại.

1.1. Định nghĩa phân cực ánh sáng

Ánh sáng tự nhiên là không phân cực, có nghĩa là nó dao động theo mọi hướng trong mặt phẳng vuông góc với phương truyền. Phân cực ánh sáng xảy ra khi một sóng ánh sáng bị giới hạn chỉ dao động trong một hướng cụ thể. Điều này có thể được thực hiện bằng cách sử dụng bộ lọc phân cực hoặc qua hiện tượng phản xạ dưới góc đặc biệt.

1.2. Nguyên lý hoạt động của phân cực ánh sáng

• Nguyên lý phân cực phẳng: Khi ánh sáng đi qua một bộ lọc phân cực, các thành phần sóng ánh sáng dao động theo phương vuông góc với trục của bộ lọc bị chặn lại, chỉ để lại các thành phần song song với trục của bộ lọc.
• Góc Brewster: Khi ánh sáng phản xạ từ bề mặt không khí - chất rắn hoặc không khí - chất lỏng ở một góc nhất định (góc Brewster), ánh sáng phản xạ sẽ bị phân cực hoàn toàn theo phương vuông góc với mặt phẳng tới.
• Hiện tượng tán xạ Rayleigh: Khi ánh sáng tán xạ qua các phân tử nhỏ hơn bước sóng của nó, ánh sáng bị tán xạ cũng sẽ bị phân cực. Hiện tượng này giải thích tại sao bầu trời có màu xanh lam và sự phân cực trong ánh sáng tán xạ.

1.3. Ví dụ minh họa

Giả sử có một chùm ánh sáng tự nhiên chiếu qua hai bộ lọc phân cực. Bộ lọc đầu tiên chỉ cho phép ánh sáng dao động theo phương ngang đi qua. Bộ lọc thứ hai, nếu xoay 90 độ so với bộ lọc đầu tiên, sẽ chặn tất cả ánh sáng đi qua, làm cho cường độ ánh sáng sau khi qua bộ lọc thứ hai bằng không.

Công thức mô tả cường độ ánh sáng sau khi qua hai bộ lọc phân cực là:

\[
I = I_0 \cos^2(\theta)
\]

Trong đó:

• \(I\) là cường độ ánh sáng sau khi qua bộ lọc thứ hai.
• \(I_0\) là cường độ ánh sáng trước khi qua bộ lọc.
• \(\theta\) là góc giữa trục của hai bộ lọc phân cực.

Phân cực ánh sáng không chỉ là một hiện tượng quang học thú vị mà còn có nhiều ứng dụng quan trọng trong đời sống và công nghệ. Dưới đây là một số ứng dụng nổi bật của phân cực ánh sáng trong các lĩnh vực khác nhau.

2.1. Kính mát phân cực

Kính mát phân cực là một trong những ứng dụng phổ biến nhất của phân cực ánh sáng. Kính mát sử dụng bộ lọc phân cực để chặn các tia sáng phản xạ từ các bề mặt phẳng như mặt nước, đường nhựa, giúp giảm độ chói và tăng cường độ tương phản, mang lại tầm nhìn rõ ràng hơn.

2.2. Công nghệ màn hình LCD

Các màn hình tinh thể lỏng (LCD) sử dụng phân cực ánh sáng để kiểm soát hiển thị. Màn hình LCD gồm hai bộ lọc phân cực đặt vuông góc với nhau, và ánh sáng truyền qua màn hình được điều khiển bởi các tinh thể lỏng, cho phép hoặc chặn ánh sáng đi qua, từ đó tạo ra hình ảnh.

2.3. Kiểm tra ứng suất trong vật liệu

Phân cực ánh sáng được sử dụng để kiểm tra ứng suất trong các vật liệu trong suốt như thủy tinh và nhựa. Khi một vật liệu bị ứng suất, nó có thể làm thay đổi trạng thái phân cực của ánh sáng, hiện tượng này được gọi là lưỡng sắc do ứng suất. Bằng cách quan sát ánh sáng phân cực qua vật liệu, ta có thể xác định các vùng ứng suất và đánh giá chất lượng của vật liệu.

2.4. Ứng dụng trong nhiếp ảnh

Phân cực ánh sáng được ứng dụng trong nhiếp ảnh để tăng cường màu sắc và giảm độ chói từ các bề mặt phản xạ như nước hoặc kính. Các bộ lọc phân cực giúp nhiếp ảnh gia chụp được những bức ảnh có màu sắc tươi sáng hơn, độ tương phản cao hơn, đặc biệt trong các cảnh ngoài trời.

2.5. Ứng dụng trong kính hiển vi phân cực

Kính hiển vi phân cực sử dụng ánh sáng phân cực để nghiên cứu các vật liệu có tính chất quang học đặc biệt. Bằng cách quan sát mẫu dưới ánh sáng phân cực, các nhà khoa học có thể phân tích cấu trúc tinh thể, nhận diện khoáng chất và các đặc tính quang học khác của mẫu vật.

2.6. Phân cực ánh sáng trong viễn thông sợi quang

Trong viễn thông sợi quang, phân cực ánh sáng đóng vai trò quan trọng trong việc tối ưu hóa hiệu suất truyền dẫn. Ánh sáng phân cực được sử dụng để giảm thiểu nhiễu và tăng cường độ ổn định của tín hiệu truyền qua các sợi quang.

Phân cực ánh sáng không chỉ là một hiện tượng quang học mà còn liên quan đến nhiều hiện tượng khác trong vật lý. Dưới đây là một số hiện tượng nổi bật liên quan đến phân cực ánh sáng.

3.1. Hiện tượng nhiễu xạ

Nhiễu xạ xảy ra khi ánh sáng đi qua một khe hẹp hoặc một vật cản, làm cho các sóng ánh sáng bị uốn cong và lan truyền ra ngoài khỏi vùng bóng tối. Trong nhiễu xạ, ánh sáng có thể bị phân cực khi đi qua các cấu trúc tinh thể, tạo ra các mô hình giao thoa đặc trưng. Điều này cho phép các nhà khoa học phân tích cấu trúc bên trong của các vật liệu dựa trên mô hình nhiễu xạ.

3.2. Hiện tượng tán sắc ánh sáng

Tán sắc ánh sáng là hiện tượng ánh sáng bị phân tách thành các thành phần màu sắc khác nhau khi đi qua một lăng kính hoặc một bề mặt khúc xạ. Ánh sáng tán sắc thường không bị phân cực, nhưng khi kết hợp với các bộ lọc phân cực, hiện tượng tán sắc có thể được quan sát dưới các góc độ khác nhau, tạo ra hiệu ứng màu sắc phong phú và thú vị.

3.3. Hiện tượng tán xạ Rayleigh

Tán xạ Rayleigh là hiện tượng ánh sáng bị tán xạ bởi các phân tử nhỏ hơn bước sóng ánh sáng, dẫn đến sự phân cực của ánh sáng tán xạ. Hiện tượng này giải thích vì sao bầu trời có màu xanh và ánh sáng mặt trời lại có màu đỏ khi hoàng hôn. Trong tán xạ Rayleigh, ánh sáng xanh bị tán xạ mạnh hơn ánh sáng đỏ, dẫn đến màu sắc đặc trưng của bầu trời.

3.4. Hiện tượng phân cực kép

Phân cực kép xảy ra khi một chùm ánh sáng bị phân cực qua hai bộ lọc phân cực đặt vuông góc với nhau. Nếu không có vật liệu lưỡng chiết giữa hai bộ lọc, không có ánh sáng nào đi qua. Tuy nhiên, khi có vật liệu lưỡng chiết, nó có thể thay đổi hướng phân cực của ánh sáng, cho phép một phần ánh sáng đi qua bộ lọc thứ hai, tạo ra các mô hình ánh sáng và bóng tối đặc trưng.

3.5. Lăng kính phân cực

Lăng kính phân cực là một thiết bị sử dụng để phân tách ánh sáng thành các tia phân cực khác nhau. Khi ánh sáng đi qua lăng kính phân cực, các thành phần sóng ánh sáng bị phân tách dựa trên hướng dao động của chúng, tạo ra hai hoặc nhiều tia sáng phân cực khác nhau. Lăng kính phân cực được sử dụng rộng rãi trong nghiên cứu quang học và các ứng dụng công nghệ.

3.6. Hiện tượng phản xạ phân cực

Phản xạ phân cực xảy ra khi ánh sáng phản xạ từ một bề mặt dưới góc Brewster, tại góc này, ánh sáng phản xạ hoàn toàn bị phân cực theo một hướng nhất định. Hiện tượng này được ứng dụng trong các thiết bị quang học để kiểm soát và điều chỉnh ánh sáng phản xạ, cũng như trong việc chế tạo các thiết bị chống chói.

Định luật Malus là một trong những định luật cơ bản của quang học, được sử dụng để mô tả mối quan hệ giữa cường độ ánh sáng khi đi qua hai bộ lọc phân cực và góc giữa trục phân cực của chúng. Định luật này được đặt theo tên nhà vật lý người Pháp Étienne-Louis Malus.

4.1. Định luật Malus

Định luật Malus phát biểu rằng: Cường độ của ánh sáng phân cực sau khi đi qua một bộ lọc phân cực thứ hai sẽ tỷ lệ thuận với bình phương của cosine của góc giữa trục phân cực của hai bộ lọc. Cụ thể, nếu cường độ ánh sáng ban đầu là \(I_0\) và góc giữa trục phân cực của hai bộ lọc là \(\theta\), thì cường độ ánh sáng \(I\) sau khi qua bộ lọc thứ hai được cho bởi công thức:

\[
I = I_0 \cos^2(\theta)
\]

Trong đó:

• \(I\) là cường độ ánh sáng sau khi qua bộ lọc thứ hai.
• \(I_0\) là cường độ ánh sáng ban đầu (trước khi qua bộ lọc).
• \(\theta\) là góc giữa trục phân cực của hai bộ lọc.

4.2. Ứng dụng của định luật Malus

• Kiểm soát cường độ ánh sáng: Định luật Malus cho phép điều chỉnh cường độ ánh sáng trong các thiết bị quang học như kính mát phân cực, bộ lọc quang học và máy ảnh.
• Phân tích tính chất quang học: Định luật này cũng được sử dụng để phân tích các tính chất quang học của vật liệu và xác định góc phân cực tối ưu trong các thí nghiệm quang học.

4.3. Công thức mở rộng

Ngoài định luật Malus, một số công thức liên quan khác cũng có thể áp dụng khi phân tích ánh sáng phân cực:

1. Khi ánh sáng phân cực đi qua nhiều bộ lọc phân cực liên tiếp, cường độ ánh sáng sau mỗi bộ lọc sẽ tiếp tục giảm theo định luật Malus, với mỗi bộ lọc có góc \(\theta_i\) so với trục của bộ lọc trước đó:

\[
I_n = I_0 \prod_{i=1}^{n} \cos^2(\theta_i)
\]

2. Khi góc giữa các trục phân cực là 90°, ánh sáng hoàn toàn bị chặn lại, cường độ ánh sáng cuối cùng sẽ là 0:

\[
I = I_0 \cos^2(90^\circ) = 0
\]

4.4. Ví dụ minh họa

Giả sử ánh sáng ban đầu có cường độ \(I_0\) và đi qua hai bộ lọc phân cực với góc giữa các trục phân cực là 45°. Cường độ ánh sáng sau bộ lọc thứ hai sẽ là:

\[
I = I_0 \cos^2(45^\circ) = I_0 \times \left(\frac{\sqrt{2}}{2}\right)^2 = \frac{I_0}{2}
\]

Như vậy, cường độ ánh sáng sau khi qua bộ lọc thứ hai giảm xuống một nửa so với cường độ ban đầu.

Nghiên cứu về phân cực ánh sáng đã trải qua nhiều giai đoạn phát triển quan trọng, bắt đầu từ những khám phá ban đầu về ánh sáng đến việc ứng dụng trong các lĩnh vực hiện đại như quang học, viễn thông, và khoa học vật liệu. Dưới đây là một cái nhìn chi tiết về lịch sử và sự phát triển của nghiên cứu trong lĩnh vực này.

5.1. Khám phá ban đầu

Khái niệm phân cực ánh sáng được bắt đầu nghiên cứu từ thế kỷ 17, khi nhà vật lý người Hà Lan Christiaan Huygens phát hiện ra rằng ánh sáng có thể biểu hiện những tính chất giống như sóng. Tuy nhiên, sự hiểu biết về phân cực chỉ thực sự tiến bộ vào đầu thế kỷ 19, khi Étienne-Louis Malus, một nhà vật lý người Pháp, phát hiện ra hiện tượng phân cực ánh sáng khi ánh sáng phản xạ từ bề mặt kính.

5.2. Sự phát triển trong thế kỷ 19

Trong thế kỷ 19, nghiên cứu về phân cực ánh sáng đã tiến một bước dài với công trình của các nhà khoa học như Augustin-Jean Fresnel và François Arago. Fresnel đã phát triển lý thuyết về sóng ánh sáng và đưa ra các công thức toán học để mô tả hiện tượng phân cực. Cũng trong thời gian này, Arago đã khám phá ra hiện tượng phân cực kép, góp phần vào việc hiểu rõ hơn về bản chất của ánh sáng.

5.3. Các nghiên cứu trong thế kỷ 20

Thế kỷ 20 chứng kiến sự bùng nổ của các nghiên cứu về phân cực ánh sáng, đặc biệt là trong các ứng dụng thực tế. Việc phát minh ra các vật liệu phân cực, như các bộ lọc phân cực và màng phân cực, đã mở ra những ứng dụng mới trong ngành công nghiệp quang học và nhiếp ảnh. Những nghiên cứu trong thời kỳ này cũng đã góp phần phát triển các công nghệ như màn hình LCD và các thiết bị chống chói.

5.4. Ứng dụng hiện đại và hướng nghiên cứu tương lai

Ngày nay, nghiên cứu về phân cực ánh sáng vẫn tiếp tục được đẩy mạnh với những ứng dụng trong viễn thông, quang học lượng tử và y học. Các nhà khoa học đang nghiên cứu cách sử dụng phân cực ánh sáng để truyền thông tin với tốc độ cao, cũng như trong việc phát triển các phương pháp chẩn đoán hình ảnh tiên tiến trong y học. Tương lai của nghiên cứu về phân cực ánh sáng hứa hẹn sẽ mang lại những phát minh và ứng dụng mang tính cách mạng trong nhiều lĩnh vực.

Phần này cung cấp một số dạng bài tập liên quan đến phân cực ánh sáng, giúp bạn nắm vững các khái niệm và ứng dụng của hiện tượng này trong thực tiễn.

6.1. Bài tập 1: Tính cường độ ánh sáng qua hai bộ lọc phân cực

Giả sử ánh sáng không phân cực có cường độ \(I_0\) đi qua hai bộ lọc phân cực có trục phân cực lệch nhau một góc \(\theta\). Hãy tính cường độ ánh sáng sau khi qua bộ lọc thứ hai.

Lời giải: Sử dụng định luật Malus, ta có cường độ ánh sáng sau khi qua bộ lọc thứ hai là:

\[
I = I_0 \cos^2(\theta)
\]

6.2. Bài tập 2: Xác định góc Brewster cho các vật liệu khác nhau

Cho biết chiết suất của không khí là \(n_1 = 1\) và của thủy tinh là \(n_2 = 1.5\). Tính góc Brewster khi ánh sáng truyền từ không khí vào thủy tinh.

Lời giải: Sử dụng công thức góc Brewster:

\[
\tan(\theta_B) = \frac{n_2}{n_1}
\]

Thay giá trị vào, ta có:

\[
\theta_B = \arctan\left(\frac{1.5}{1}\right) \approx 56.3^\circ
\]

6.3. Bài tập 3: Tính góc phân cực trong các môi trường khác nhau

Một tia sáng truyền từ không khí vào nước với chiết suất \(n = 1.33\). Hãy tính góc tới mà tại đó ánh sáng phản xạ bị phân cực hoàn toàn.

Lời giải: Góc phân cực (góc Brewster) được tính bằng:

\[
\theta_B = \arctan\left(\frac{1.33}{1}\right) \approx 53.1^\circ
\]

6.4. Bài tập 4: Phân tích ánh sáng phân cực qua lăng kính

Một chùm ánh sáng không phân cực đi qua một lăng kính có góc chiết quang \(A\) và chiết suất \(n\). Hãy xác định góc phân cực và cường độ ánh sáng sau khi đi qua lăng kính.

Hướng dẫn: Áp dụng định luật khúc xạ và hiện tượng phân cực để tính toán.

6.5. Bài tập 5: Sử dụng định luật Malus để xác định cường độ ánh sáng

Một ánh sáng phân cực phẳng có cường độ \(I_0\) chiếu qua hai bộ lọc phân cực với góc lệch giữa các trục phân cực là \(45^\circ\). Hãy tính cường độ ánh sáng sau khi qua cả hai bộ lọc.

Lời giải: Áp dụng định luật Malus:

\[
I = I_0 \cos^2(45^\circ) = \frac{I_0}{2}
\]

6.6. Bài tập 6: Ứng dụng phân cực trong quang học nhiếp ảnh

Một nhiếp ảnh gia muốn giảm độ chói từ ánh sáng phản xạ trên mặt nước. Hãy giải thích cách sử dụng kính phân cực để đạt được hiệu ứng này và tính góc đặt kính phân cực phù hợp.

Hướng dẫn: Sử dụng kính phân cực với trục phân cực vuông góc với hướng phân cực của ánh sáng phản xạ.

6.7. Bài tập 7: Phân cực ánh sáng và ứng dụng trong công nghệ LCD

Giải thích cơ chế hoạt động của màn hình LCD dựa trên hiện tượng phân cực ánh sáng và đề xuất một bài toán liên quan đến việc điều chỉnh cường độ ánh sáng qua màn hình.

6.8. Bài tập 8: Xác định phân cực ánh sáng từ mặt nước

Một chùm ánh sáng chiếu xuống mặt nước và bị phản xạ. Hãy xác định điều kiện để ánh sáng phản xạ bị phân cực hoàn toàn và tính toán góc tới tương ứng.

6.9. Bài tập 9: Phân tích hiện tượng phân cực trong kính mát

Một người sử dụng kính mát phân cực để giảm độ chói từ mặt đường. Giải thích hiện tượng này và tính toán góc phân cực thích hợp của kính mát.

6.10. Bài tập 10: Tính toán cường độ ánh sáng qua lớp phủ phân cực

Một lớp phủ phân cực được đặt trên bề mặt của một màn hình hiển thị. Hãy tính cường độ ánh sáng sau khi đi qua lớp phủ này nếu biết rằng ánh sáng ban đầu có cường độ \(I_0\) và góc phân cực là \(30^\circ\).

Lời giải: Cường độ ánh sáng sau khi qua lớp phủ được tính bằng:

\[
I = I_0 \cos^2(30^\circ) \approx 0.75 I_0
\]