Chủ đề dụng cụ quang học là gì: Dụng cụ quang học là gì? Đây là câu hỏi mà nhiều người quan tâm khi nhắc đến những thiết bị sử dụng nguyên lý ánh sáng. Bài viết này sẽ giới thiệu về các loại dụng cụ quang học phổ biến, nguyên lý hoạt động, và ứng dụng của chúng trong đời sống, y tế, công nghiệp, và nghiên cứu khoa học. Khám phá ngay để hiểu rõ hơn về vai trò quan trọng của quang học trong cuộc sống hàng ngày!
Mục lục
- Dụng cụ quang học là gì?
- Giới thiệu về dụng cụ quang học
- Ứng dụng của dụng cụ quang học trong đời sống và công nghiệp
- Tầm quan trọng của quang học trong nghiên cứu khoa học
- 10 Dạng bài tập Toán và Vật lý về Quang học có lời giải
- Bài tập 1: Tính góc khúc xạ của ánh sáng qua lăng kính
- Bài tập 2: Xác định tiêu cự của thấu kính hội tụ
- Bài tập 3: Tính độ phóng đại của kính hiển vi
- Bài tập 4: Phân tích quang phổ ánh sáng từ nguồn sáng
- Bài tập 5: Tính thời gian ánh sáng truyền qua môi trường khác nhau
- Bài tập 6: Giải thích hiện tượng giao thoa ánh sáng qua khe hẹp
- Bài tập 7: Tính công suất quang học của một hệ thấu kính
- Bài tập 8: Xác định bước sóng ánh sáng qua thí nghiệm nhiễu xạ
- Bài tập 9: Tính khoảng cách giữa hai vạch sáng trong thí nghiệm Young
- Bài tập 10: Phân tích và giải thích hiện tượng phân cực ánh sáng
Dụng cụ quang học là gì?
Dụng cụ quang học là những thiết bị và công cụ sử dụng các nguyên lý quang học để thực hiện các chức năng nhất định, chủ yếu liên quan đến ánh sáng và các tính chất của nó. Các dụng cụ này được sử dụng rộng rãi trong nhiều lĩnh vực như y tế, giáo dục, khoa học, công nghệ và đời sống hàng ngày.
Các loại dụng cụ quang học phổ biến
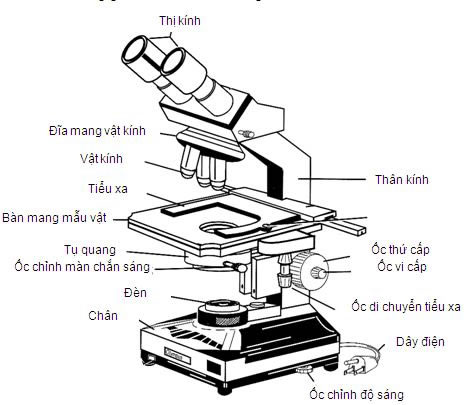
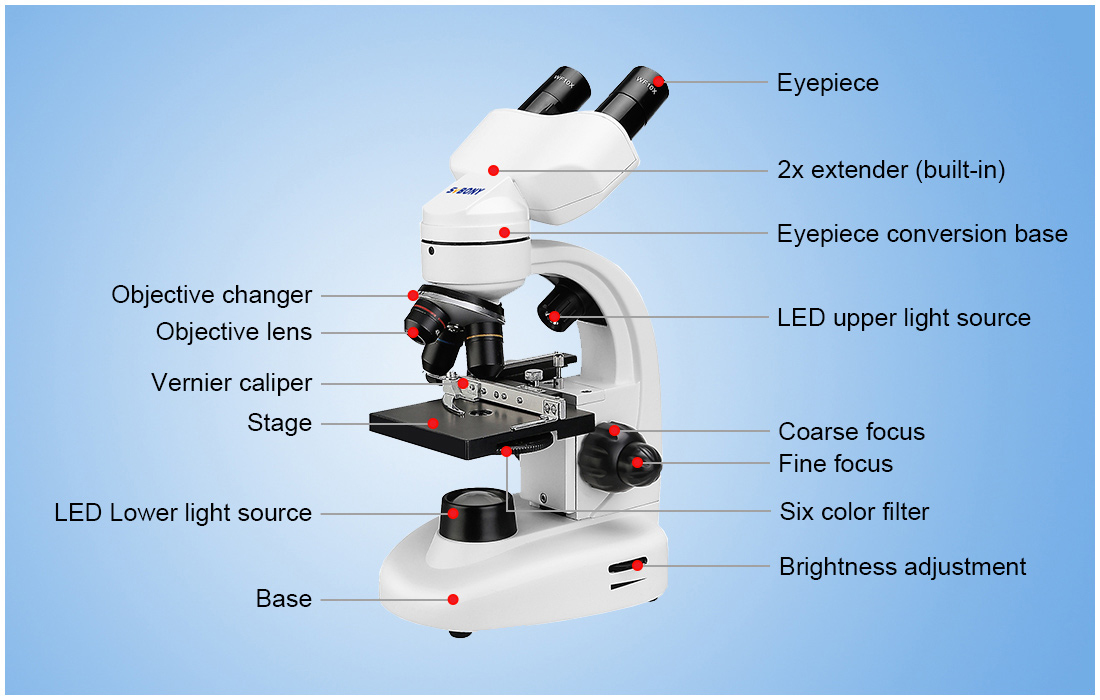
- Kính hiển vi: Dụng cụ này cho phép quan sát các vật thể nhỏ mà mắt thường không thể nhìn thấy, như tế bào, vi khuẩn. Kính hiển vi thường được sử dụng trong các phòng thí nghiệm, trường học, và cơ sở y tế.
- Kính thiên văn: Sử dụng để quan sát các thiên thể xa xôi như sao, hành tinh và các thiên hà. Kính thiên văn giúp con người khám phá vũ trụ và nghiên cứu các hiện tượng thiên văn.
- Kính lúp: Là loại kính có thấu kính lồi giúp phóng to hình ảnh của vật thể nhỏ để dễ dàng quan sát. Kính lúp thường được dùng trong các ngành như sửa chữa đồng hồ, kiểm tra chi tiết kỹ thuật, và giảng dạy khoa học.
- Máy ảnh: Dụng cụ quang học này sử dụng hệ thống ống kính để thu nhận và lưu giữ hình ảnh. Máy ảnh được sử dụng rộng rãi trong nhiếp ảnh, nghệ thuật và các lĩnh vực liên quan đến truyền thông.
- Thiết bị đo khoảng cách: Các thiết bị như laser đo khoảng cách sử dụng nguyên lý phản xạ và khúc xạ của ánh sáng để đo khoảng cách chính xác, thường được sử dụng trong xây dựng và nghiên cứu khoa học.
Nguyên lý hoạt động của dụng cụ quang học
Các dụng cụ quang học hoạt động dựa trên các nguyên lý cơ bản của quang học, bao gồm khúc xạ, phản xạ, tán xạ, và giao thoa ánh sáng. Ví dụ, kính thiên văn sử dụng các thấu kính hoặc gương để thu nhận và hội tụ ánh sáng từ các vật thể ở xa, trong khi kính hiển vi sử dụng thấu kính để phóng đại hình ảnh của các vật thể nhỏ.
Ứng dụng của dụng cụ quang học trong đời sống
- Y tế: Dụng cụ quang học như kính hiển vi, máy quang phổ, và thiết bị nội soi được sử dụng rộng rãi để chẩn đoán và điều trị bệnh.
- Giáo dục: Các dụng cụ như kính hiển vi và kính lúp giúp học sinh hiểu rõ hơn về cấu trúc vi mô của các sinh vật và vật liệu.
- Khoa học và công nghệ: Quang học là nền tảng cho nhiều thiết bị đo lường, cảm biến và các hệ thống truyền thông như cáp quang.
- Giải trí: Công nghệ quang học được áp dụng trong các thiết bị giải trí như máy ảnh, máy quay phim, và các hệ thống thực tế ảo.
Kết luận
Dụng cụ quang học đóng vai trò quan trọng trong nhiều lĩnh vực, từ khoa học, y tế đến công nghệ và đời sống hàng ngày. Hiểu biết về quang học không chỉ giúp cải thiện chất lượng cuộc sống mà còn thúc đẩy sự phát triển của nhiều công nghệ tiên tiến.

.png)
Giới thiệu về dụng cụ quang học
Dụng cụ quang học là những thiết bị hoặc công cụ sử dụng nguyên lý của ánh sáng để thực hiện các chức năng cụ thể như phóng đại hình ảnh, phân tích ánh sáng, hoặc đo lường khoảng cách. Các dụng cụ này dựa vào các hiện tượng quang học cơ bản như khúc xạ, phản xạ, giao thoa và nhiễu xạ để hoạt động. Chúng được ứng dụng rộng rãi trong nhiều lĩnh vực, từ nghiên cứu khoa học, y tế đến công nghiệp và đời sống hàng ngày.
Một số đặc điểm quan trọng của dụng cụ quang học bao gồm:
- Phân loại: Dụng cụ quang học có thể được phân loại thành nhiều nhóm khác nhau như kính hiển vi, kính thiên văn, kính lúp, và các thiết bị đo quang học.
- Nguyên lý hoạt động: Các dụng cụ này hoạt động dựa trên nguyên lý của sự khúc xạ và phản xạ ánh sáng, cho phép thay đổi hướng đi của tia sáng để quan sát hoặc đo lường các đối tượng không thể nhìn thấy bằng mắt thường.
- Ứng dụng: Dụng cụ quang học được ứng dụng rộng rãi trong nhiều lĩnh vực, từ y tế (máy nội soi, kính hiển vi), công nghiệp (máy đo quang học, thiết bị kiểm tra chất lượng) đến giáo dục và nghiên cứu khoa học (kính thiên văn, kính hiển vi điện tử).
Dưới đây là một số ví dụ về dụng cụ quang học và ứng dụng của chúng:
| Dụng cụ quang học | Ứng dụng |
|---|---|
| Kính hiển vi | Quan sát vi sinh vật, nghiên cứu tế bào và các mẫu vật nhỏ trong phòng thí nghiệm. |
| Kính thiên văn | Quan sát các thiên thể xa xôi trong vũ trụ như sao, hành tinh, và thiên hà. |
| Kính lúp | Phóng đại các đối tượng nhỏ để nhìn rõ hơn, thường dùng trong sửa chữa đồng hồ, đọc bản đồ, và kiểm tra các chi tiết nhỏ. |
| Máy ảnh | Ghi lại hình ảnh trong nhiếp ảnh, điện ảnh và các ứng dụng truyền thông khác. |
Quang học không chỉ là một lĩnh vực khoa học nghiên cứu về ánh sáng mà còn là nền tảng của nhiều công nghệ tiên tiến. Các dụng cụ quang học đã và đang đóng góp quan trọng vào sự phát triển của nhiều ngành công nghiệp và khoa học, từ y học, truyền thông đến nghiên cứu vũ trụ. Việc hiểu rõ về các dụng cụ này giúp chúng ta ứng dụng hiệu quả hơn trong công việc và cuộc sống.
Ứng dụng của dụng cụ quang học trong đời sống và công nghiệp
Dụng cụ quang học có vai trò quan trọng trong cả đời sống hàng ngày và nhiều ngành công nghiệp. Chúng được sử dụng để cải thiện khả năng quan sát, đo lường, và phân tích ánh sáng, giúp nâng cao hiệu suất làm việc và cải thiện chất lượng cuộc sống. Dưới đây là các ứng dụng phổ biến của dụng cụ quang học:
- Ứng dụng trong y tế:
- Kính hiển vi: Được sử dụng rộng rãi trong các phòng thí nghiệm y tế để quan sát tế bào, vi khuẩn, và các mẫu sinh học khác, giúp chẩn đoán và nghiên cứu các bệnh lý. Kính hiển vi điện tử còn cho phép nhìn rõ cấu trúc tế bào với độ phóng đại cao.
- Máy nội soi: Dụng cụ này cho phép các bác sĩ quan sát bên trong cơ thể mà không cần phẫu thuật xâm lấn, giúp chẩn đoán chính xác và giảm thiểu nguy cơ cho bệnh nhân.
- Ứng dụng trong công nghiệp:
- Máy đo khoảng cách bằng laser: Được sử dụng trong xây dựng và khảo sát để đo khoảng cách chính xác, giúp lập kế hoạch xây dựng và đảm bảo chất lượng công trình. Thiết bị này cũng được sử dụng trong các hệ thống tự động hóa để đo lường và kiểm tra sản phẩm.
- Máy quang phổ: Máy quang phổ được sử dụng để phân tích thành phần hóa học của vật liệu trong công nghiệp hóa chất và thực phẩm, giúp đảm bảo chất lượng và an toàn sản phẩm.
- Ứng dụng trong giáo dục và nghiên cứu khoa học:
- Kính thiên văn: Kính thiên văn giúp các nhà thiên văn học quan sát và nghiên cứu các thiên thể trong vũ trụ. Thiết bị này cung cấp thông tin quan trọng về cấu trúc và sự hình thành của các hành tinh, sao, và thiên hà.
- Kính hiển vi: Trong nghiên cứu khoa học, kính hiển vi giúp phân tích và nghiên cứu cấu trúc của vật liệu, sinh vật học, và nhiều lĩnh vực khác. Các trường học và đại học sử dụng kính hiển vi để giảng dạy và thực hành nghiên cứu khoa học.
- Ứng dụng trong đời sống hàng ngày:
- Kính đeo mắt: Kính đeo mắt, bao gồm kính cận, kính viễn, và kính lão, giúp điều chỉnh tầm nhìn cho những người có vấn đề về thị lực, cải thiện chất lượng cuộc sống hàng ngày.
- Kính mát: Kính mát không chỉ bảo vệ mắt khỏi tia UV có hại từ ánh sáng mặt trời mà còn giúp giảm chói, tạo cảm giác thoải mái khi lái xe và tham gia các hoạt động ngoài trời.
- Máy ảnh: Máy ảnh sử dụng hệ thống quang học để ghi lại hình ảnh, được sử dụng rộng rãi trong nhiếp ảnh, truyền thông, và điện ảnh. Máy ảnh kỹ thuật số và điện thoại thông minh ngày nay kết hợp công nghệ quang học tiên tiến để cung cấp hình ảnh chất lượng cao.
Nhờ vào các nguyên lý hoạt động hiệu quả, dụng cụ quang học đã trở thành những công cụ không thể thiếu trong nhiều lĩnh vực, giúp cải thiện không chỉ khả năng quan sát và nghiên cứu mà còn nâng cao chất lượng cuộc sống và hiệu suất làm việc trong nhiều ngành công nghiệp.

Tầm quan trọng của quang học trong nghiên cứu khoa học
Quang học là một lĩnh vực quan trọng trong vật lý và khoa học tự nhiên, đóng vai trò then chốt trong việc khám phá và hiểu biết sâu sắc về vũ trụ cũng như các hiện tượng tự nhiên. Dụng cụ quang học, dựa trên các nguyên lý cơ bản của quang học, đã cung cấp cho các nhà khoa học những công cụ mạnh mẽ để nghiên cứu và mở rộng kiến thức của con người. Dưới đây là một số lý do tại sao quang học quan trọng trong nghiên cứu khoa học:
- Nghiên cứu vũ trụ và thiên văn học:
Kính thiên văn và các thiết bị quan sát không gian khác đã cho phép con người khám phá và nghiên cứu sâu hơn về vũ trụ. Nhờ vào quang học, chúng ta có thể quan sát và phân tích các hiện tượng xa xôi như sự hình thành sao, hố đen, và các thiên hà. Các phương pháp quang phổ học giúp phân tích thành phần hóa học của các thiên thể, từ đó hiểu rõ hơn về sự phát triển và tiến hóa của vũ trụ.
- Phân tích và chẩn đoán trong y học:
Trong y học, các công cụ quang học như kính hiển vi và máy nội soi đóng vai trò quan trọng trong việc chẩn đoán và nghiên cứu bệnh lý. Kính hiển vi cho phép các nhà khoa học và bác sĩ quan sát tế bào và mô với độ phân giải cao, từ đó phát hiện các dấu hiệu bệnh lý và nghiên cứu các tác nhân gây bệnh. Máy nội soi giúp thăm dò bên trong cơ thể mà không cần phẫu thuật, mang lại nhiều lợi ích trong việc chẩn đoán và điều trị bệnh.
- Nghiên cứu vật liệu và hóa học:
Các dụng cụ quang học như máy quang phổ, kính hiển vi điện tử và các thiết bị phân tích quang học khác đóng vai trò quan trọng trong nghiên cứu vật liệu và hóa học. Chúng giúp phân tích thành phần, cấu trúc, và tính chất của vật liệu, từ đó phát triển các vật liệu mới và cải tiến công nghệ hiện có. Trong hóa học, quang học giúp xác định thành phần hóa học và cấu trúc phân tử của các chất, hỗ trợ quá trình nghiên cứu và phát triển sản phẩm mới.
- Phát triển công nghệ tiên tiến:
Quang học đóng vai trò quan trọng trong việc phát triển các công nghệ tiên tiến như truyền thông quang học, công nghệ laser, và thiết bị cảm biến quang học. Các tiến bộ trong công nghệ quang học đã cải thiện đáng kể khả năng truyền tải dữ liệu, tạo ra các thiết bị y tế tiên tiến, và nâng cao khả năng cảm biến và nhận dạng trong nhiều lĩnh vực khác nhau.
- Đo lường và tiêu chuẩn hóa:
Các dụng cụ quang học như interferometer (giao thoa kế) và các thiết bị đo lường quang học khác được sử dụng để đo lường chính xác các đại lượng vật lý như khoảng cách, chiều dài, và thời gian. Những thiết bị này cung cấp độ chính xác cao, giúp tiêu chuẩn hóa các phép đo trong nghiên cứu khoa học và công nghiệp.
Tóm lại, quang học không chỉ là một lĩnh vực nghiên cứu cơ bản trong khoa học mà còn là công cụ quan trọng giúp con người khám phá, hiểu biết, và ứng dụng vào nhiều lĩnh vực khác nhau từ vũ trụ học, y học, hóa học đến công nghệ tiên tiến. Vai trò của quang học trong nghiên cứu khoa học là không thể thay thế, góp phần thúc đẩy sự tiến bộ và đổi mới trong mọi lĩnh vực của cuộc sống.

10 Dạng bài tập Toán và Vật lý về Quang học có lời giải

Bài tập 1: Tính góc khúc xạ của ánh sáng qua lăng kính
Trong bài tập này, chúng ta sẽ tìm hiểu cách tính góc khúc xạ của ánh sáng khi đi qua một lăng kính tam giác. Lăng kính là một dụng cụ quang học cơ bản được sử dụng để phân tích ánh sáng thành các thành phần màu sắc của nó, cũng như để thay đổi hướng truyền của ánh sáng.
1. Đề bài
Một tia sáng đơn sắc có góc tới \(i_1 = 30^\circ\) chiếu vào mặt bên của một lăng kính tam giác đều với góc chiết quang \(A = 60^\circ\). Chỉ số chiết suất của lăng kính là \(n = 1.5\). Hãy tính góc khúc xạ của tia sáng khi đi qua lăng kính.
2. Hướng dẫn giải
Để giải bài toán này, chúng ta sẽ thực hiện các bước sau:
- Tính góc khúc xạ \(r_1\) tại mặt đầu tiên của lăng kính.
- Tính góc khúc xạ \(r_2\) tại mặt thứ hai của lăng kính.
- Sử dụng công thức khúc xạ ánh sáng (định luật Snell) để xác định các giá trị cần thiết.
3. Giải chi tiết
Bước 1: Tính góc khúc xạ \(r_1\) tại mặt đầu tiên của lăng kính.
Theo định luật khúc xạ ánh sáng (định luật Snell), chúng ta có:
\[ n_1 \sin i_1 = n_2 \sin r_1 \]
Ở đây:
- \(n_1 = 1\) (chỉ số chiết suất của không khí)
- \(i_1 = 30^\circ\) (góc tới)
- \(n_2 = 1.5\) (chỉ số chiết suất của lăng kính)
Thay các giá trị vào công thức, ta có:
\[ 1 \times \sin 30^\circ = 1.5 \times \sin r_1 \]
Từ đó tính được:
\[ \sin r_1 = \frac{\sin 30^\circ}{1.5} = \frac{0.5}{1.5} \approx 0.333 \]
Vậy:
\[ r_1 = \arcsin(0.333) \approx 19.47^\circ \]
Bước 2: Tính góc khúc xạ \(r_2\) tại mặt thứ hai của lăng kính.
Góc khúc xạ bên trong lăng kính được xác định bởi công thức:
\[ r_1 + r_2 = A \]
Thay các giá trị đã biết, ta có:
\[ r_2 = A - r_1 = 60^\circ - 19.47^\circ \approx 40.53^\circ \]
Bước 3: Tính góc khúc xạ cuối cùng khi tia sáng ra khỏi lăng kính.
Sử dụng định luật khúc xạ tại mặt thứ hai của lăng kính:
\[ n_2 \sin r_2 = n_1 \sin i_2 \]
Thay vào công thức, ta có:
\[ 1.5 \times \sin 40.53^\circ = 1 \times \sin i_2 \]
Tính được:
\[ \sin i_2 \approx 0.975 \]
Vậy:
\[ i_2 = \arcsin(0.975) \approx 77.62^\circ \]
4. Kết quả
Góc khúc xạ của ánh sáng khi đi qua lăng kính là khoảng \(77.62^\circ\). Đây là kết quả cuối cùng của bài toán.
XEM THÊM:
Bài tập 2: Xác định tiêu cự của thấu kính hội tụ
Tiêu cự của thấu kính hội tụ là một trong những thông số quan trọng để xác định khả năng tập trung ánh sáng của thấu kính đó. Trong bài tập này, chúng ta sẽ tìm hiểu cách xác định tiêu cự của một thấu kính hội tụ bằng phương pháp thực nghiệm đơn giản.
Phương pháp thí nghiệm
Để xác định tiêu cự của thấu kính hội tụ, chúng ta có thể sử dụng phương pháp tạo ảnh trên màn và đo khoảng cách từ thấu kính đến ảnh. Dưới đây là các bước cụ thể:
- Chuẩn bị một nguồn sáng (ví dụ: một ngọn nến) và đặt nó trước thấu kính hội tụ.
- Đặt một màn chắn tại vị trí sao cho ánh sáng từ nguồn sáng có thể chiếu qua thấu kính và tạo ra ảnh trên màn.
- Di chuyển màn ra xa hoặc lại gần thấu kính cho đến khi ảnh hiện ra rõ nét trên màn. Đo khoảng cách từ thấu kính đến màn chắn và ghi lại giá trị này, gọi là \(d_i\) (khoảng cách ảnh).
- Đo khoảng cách từ nguồn sáng đến thấu kính, gọi là \(d_o\) (khoảng cách vật).
Công thức tính tiêu cự
Sau khi đo được \(d_i\) và \(d_o\), chúng ta có thể sử dụng công thức của thấu kính để tính tiêu cự \(f\) như sau:
Trong đó:
- \(f\): Tiêu cự của thấu kính (đơn vị: mét).
- \(d_o\): Khoảng cách từ thấu kính đến vật (đơn vị: mét).
- \(d_i\): Khoảng cách từ thấu kính đến ảnh (đơn vị: mét).
Ví dụ minh họa
Giả sử chúng ta có các giá trị sau:
- \(d_o = 0.3 \, \text{m}\) (khoảng cách từ nguồn sáng đến thấu kính).
- \(d_i = 0.6 \, \text{m}\) (khoảng cách từ thấu kính đến màn chắn).
Áp dụng công thức:
Vậy tiêu cự của thấu kính là 0.2 mét.
Kết luận
Xác định tiêu cự của thấu kính hội tụ là một kỹ năng cơ bản trong quang học, giúp chúng ta hiểu rõ hơn về cách mà ánh sáng tương tác với thấu kính để tạo ra hình ảnh. Bằng cách thực hiện các thí nghiệm đơn giản như trên, chúng ta có thể dễ dàng tính toán và hiểu về tính chất của thấu kính một cách thực tế.

Bài tập 3: Tính độ phóng đại của kính hiển vi
Kính hiển vi là một dụng cụ quang học quan trọng giúp chúng ta quan sát các vật thể có kích thước rất nhỏ mà mắt thường không thể thấy được. Độ phóng đại của kính hiển vi là một yếu tố quan trọng, quyết định khả năng phóng to của kính. Bài tập này sẽ hướng dẫn cách tính độ phóng đại của kính hiển vi.
Cách tính độ phóng đại của kính hiển vi
Kính hiển vi thường gồm hai bộ phận quang học chính: thị kính và vật kính. Độ phóng đại tổng cộng của kính hiển vi được tính bằng cách nhân độ phóng đại của thị kính và vật kính. Công thức tính như sau:
Trong đó:
- \(M\): Độ phóng đại tổng cộng của kính hiển vi.
- \(M_o\): Độ phóng đại của vật kính.
- \(M_e\): Độ phóng đại của thị kính.
Ví dụ minh họa
Giả sử chúng ta có một kính hiển vi với các thông số sau:
- Độ phóng đại của vật kính \(M_o = 40\) lần.
- Độ phóng đại của thị kính \(M_e = 10\) lần.
Áp dụng công thức tính độ phóng đại:
Vậy, độ phóng đại tổng cộng của kính hiển vi là 400 lần.
Các yếu tố ảnh hưởng đến độ phóng đại
Độ phóng đại của kính hiển vi phụ thuộc vào hai yếu tố chính:
- Độ phóng đại của vật kính: Vật kính có độ phóng đại cao hơn sẽ giúp phóng to vật thể nhiều hơn.
- Độ phóng đại của thị kính: Thị kính có độ phóng đại lớn hơn sẽ tăng cường khả năng phóng đại của kính hiển vi.
Kết luận
Hiểu rõ cách tính độ phóng đại của kính hiển vi và các yếu tố ảnh hưởng là cần thiết để lựa chọn đúng loại kính hiển vi phù hợp với nhu cầu quan sát cụ thể. Việc sử dụng kính hiển vi hiệu quả sẽ giúp chúng ta khám phá thế giới vi mô một cách chi tiết và chính xác.

Bài tập 4: Phân tích quang phổ ánh sáng từ nguồn sáng
Phân tích quang phổ ánh sáng là một kỹ thuật quan trọng trong quang học, giúp chúng ta hiểu rõ hơn về tính chất và thành phần của ánh sáng phát ra từ một nguồn sáng cụ thể. Bài tập này sẽ hướng dẫn cách phân tích quang phổ ánh sáng từ một nguồn sáng bằng các dụng cụ quang học cơ bản.
Nguyên lý phân tích quang phổ ánh sáng
Khi ánh sáng từ một nguồn sáng chiếu qua một lăng kính hoặc một mạng nhiễu xạ, nó sẽ bị phân tách thành các thành phần màu sắc khác nhau, tạo thành một dải quang phổ. Mỗi màu sắc trong dải quang phổ tương ứng với một bước sóng cụ thể, và thông qua việc đo đạc các bước sóng này, chúng ta có thể phân tích thành phần của ánh sáng.
Các bước thực hiện thí nghiệm phân tích quang phổ
- Chuẩn bị dụng cụ: Một nguồn sáng (ví dụ: đèn huỳnh quang hoặc đèn sợi đốt), một lăng kính hoặc một mạng nhiễu xạ, và một màn để quan sát quang phổ.
- Thiết lập thí nghiệm: Đặt lăng kính hoặc mạng nhiễu xạ trên đường đi của tia sáng phát ra từ nguồn sáng. Đặt màn ở vị trí sao cho có thể quan sát rõ ràng quang phổ ánh sáng được tạo ra.
- Quan sát và ghi lại kết quả: Khi ánh sáng đi qua lăng kính hoặc mạng nhiễu xạ, nó sẽ bị phân tách thành một dải màu sắc. Quan sát các màu sắc xuất hiện trên màn và ghi lại vị trí và cường độ của từng màu sắc.
- Phân tích quang phổ: Đo các bước sóng tương ứng với từng màu sắc trong quang phổ. Sử dụng các công cụ đo đạc hoặc bảng dữ liệu quang phổ để xác định bước sóng chính xác của từng màu sắc.
Ví dụ minh họa
Giả sử chúng ta có một nguồn sáng trắng và sử dụng lăng kính để phân tích quang phổ. Trên màn, chúng ta quan sát thấy các màu sắc từ đỏ, cam, vàng, lục, lam, chàm, đến tím. Mỗi màu sắc này tương ứng với một dải bước sóng cụ thể:
- Màu đỏ: \[620 - 750 \, \text{nm}\]
- Màu cam: \[590 - 620 \, \text{nm}\]
- Màu vàng: \[570 - 590 \, \text{nm}\]
- Màu lục: \[495 - 570 \, \text{nm}\]
- Màu lam: \[450 - 495 \, \text{nm}\]
- Màu chàm: \[430 - 450 \, \text{nm}\]
- Màu tím: \[380 - 430 \, \text{nm}\]
Kết luận
Phân tích quang phổ ánh sáng từ một nguồn sáng cho phép chúng ta hiểu rõ hơn về tính chất của nguồn sáng đó. Kỹ thuật này có ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý, hóa học, và thiên văn học. Thông qua việc phân tích quang phổ, chúng ta có thể xác định được thành phần hóa học của các chất, đo đạc nhiệt độ của các ngôi sao, và nghiên cứu các hiện tượng tự nhiên khác.
Bài tập 5: Tính thời gian ánh sáng truyền qua môi trường khác nhau
Ánh sáng truyền qua các môi trường khác nhau với tốc độ khác nhau do tính chất vật lý của mỗi môi trường. Việc tính toán thời gian ánh sáng truyền qua các môi trường này là rất quan trọng trong nghiên cứu quang học. Bài tập này sẽ hướng dẫn cách tính thời gian ánh sáng truyền qua hai môi trường khác nhau.
Nguyên lý cơ bản
Thời gian ánh sáng truyền qua một môi trường phụ thuộc vào tốc độ ánh sáng trong môi trường đó và độ dày của môi trường. Công thức tính thời gian \(t\) để ánh sáng truyền qua một đoạn đường \(d\) trong môi trường có chiết suất \(n\) như sau:
Trong đó:
- \(t\): Thời gian ánh sáng truyền qua (đơn vị: giây).
- \(d\): Độ dài đoạn đường ánh sáng truyền qua (đơn vị: mét).
- \(v\): Tốc độ ánh sáng trong môi trường (đơn vị: mét/giây).
Tốc độ ánh sáng trong môi trường được tính bằng công thức:
Trong đó:
- \(c\): Tốc độ ánh sáng trong chân không (\(c \approx 3 \times 10^8\) m/s).
- \(n\): Chiết suất của môi trường.
Các bước thực hiện tính toán
- Xác định chiết suất của môi trường: Tìm giá trị chiết suất của các môi trường mà ánh sáng truyền qua. Ví dụ: chiết suất của nước là khoảng 1.33, của thủy tinh là khoảng 1.5.
- Tính tốc độ ánh sáng trong môi trường: Sử dụng công thức \(v = \frac{c}{n}\) để tính tốc độ ánh sáng trong mỗi môi trường.
- Đo khoảng cách ánh sáng truyền qua: Xác định độ dài đoạn đường ánh sáng đi qua trong mỗi môi trường.
- Tính thời gian truyền qua mỗi môi trường: Sử dụng công thức \(t = \frac{d}{v}\) để tính thời gian truyền qua cho mỗi đoạn đường.
- Tính tổng thời gian: Cộng thời gian truyền qua các môi trường để có tổng thời gian ánh sáng truyền qua tất cả các môi trường.
Ví dụ minh họa
Giả sử ánh sáng truyền qua hai môi trường: không khí (chiết suất \(n_1 = 1.0\)) và nước (chiết suất \(n_2 = 1.33\)). Khoảng cách ánh sáng truyền qua không khí là \(d_1 = 100\) cm và qua nước là \(d_2 = 200\) cm.
- Tốc độ ánh sáng trong không khí: \(v_1 = \frac{3 \times 10^8}{1.0} = 3 \times 10^8\) m/s.
- Tốc độ ánh sáng trong nước: \(v_2 = \frac{3 \times 10^8}{1.33} \approx 2.26 \times 10^8\) m/s.
- Thời gian truyền qua không khí: \(t_1 = \frac{100 \times 10^{-2}}{3 \times 10^8} \approx 3.33 \times 10^{-9}\) giây.
- Thời gian truyền qua nước: \(t_2 = \frac{200 \times 10^{-2}}{2.26 \times 10^8} \approx 8.85 \times 10^{-9}\) giây.
Tổng thời gian ánh sáng truyền qua hai môi trường:
Kết luận
Tính toán thời gian ánh sáng truyền qua các môi trường khác nhau giúp chúng ta hiểu rõ hơn về tốc độ truyền dẫn ánh sáng và các hiện tượng liên quan đến quang học. Việc này không chỉ quan trọng trong nghiên cứu khoa học mà còn có ứng dụng thực tế trong kỹ thuật và công nghệ.

Bài tập 6: Giải thích hiện tượng giao thoa ánh sáng qua khe hẹp
Hiện tượng giao thoa ánh sáng là một trong những hiện tượng cơ bản và quan trọng trong quang học, cho thấy tính chất sóng của ánh sáng. Khi ánh sáng truyền qua một hoặc nhiều khe hẹp, nó có thể tạo ra các vân sáng và vân tối do sự chồng chập của các sóng ánh sáng. Bài tập này sẽ giải thích chi tiết hiện tượng giao thoa ánh sáng qua khe hẹp.
Nguyên lý hiện tượng giao thoa ánh sáng
Giao thoa ánh sáng xảy ra khi hai hoặc nhiều sóng ánh sáng gặp nhau và chồng chập lên nhau. Có hai loại giao thoa chính:
- Giao thoa tăng cường: Khi các đỉnh sóng gặp nhau, chúng tạo ra vân sáng (độ sáng tăng cường).
- Giao thoa triệt tiêu: Khi đỉnh sóng này gặp đáy sóng kia, chúng tạo ra vân tối (ánh sáng bị triệt tiêu).
Hiện tượng giao thoa qua khe hẹp
Khi ánh sáng từ một nguồn đơn sắc đi qua hai khe hẹp song song và rất gần nhau, hai chùm tia sáng này sẽ giao thoa với nhau, tạo ra một mô hình các vân sáng và vân tối trên màn quan sát.
Các vân sáng và tối được tạo ra bởi sự khác nhau về đường đi của các tia sáng từ hai khe đến màn. Khoảng cách giữa các vân có thể được tính toán bằng công thức:
Trong đó:
- \(\Delta x\): Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp.
- \(\lambda\): Bước sóng của ánh sáng (đơn vị: mét).
- \(L\): Khoảng cách từ khe đến màn quan sát (đơn vị: mét).
- \(d\): Khoảng cách giữa hai khe hẹp (đơn vị: mét).
Các bước thực hiện thí nghiệm
- Chuẩn bị dụng cụ: Nguồn sáng đơn sắc (như laser), hai khe hẹp song song, màn quan sát, thước đo.
- Thiết lập thí nghiệm: Đặt nguồn sáng sao cho ánh sáng chiếu qua hai khe hẹp và tạo ra các vân giao thoa trên màn.
- Quan sát mô hình giao thoa: Trên màn quan sát, chú ý đến các vân sáng và tối xuất hiện. Ghi lại khoảng cách giữa các vân sáng hoặc vân tối liên tiếp.
- Tính toán khoảng cách giữa các vân: Sử dụng công thức \(\Delta x = \frac{\lambda L}{d}\) để tính toán khoảng cách giữa các vân sáng hoặc tối.
Ví dụ minh họa
Giả sử chúng ta có một nguồn sáng laser đơn sắc với bước sóng \(\lambda = 500\) nm, khoảng cách từ khe đến màn là \(L = 2\) m, và khoảng cách giữa hai khe hẹp là \(d = 0.1\) mm.
- Chuyển đổi đơn vị: \(\lambda = 500\) nm = \(500 \times 10^{-9}\) m, \(d = 0.1\) mm = \(0.1 \times 10^{-3}\) m.
- Tính khoảng cách giữa các vân sáng hoặc tối liên tiếp: \[ \Delta x = \frac{\lambda L}{d} = \frac{500 \times 10^{-9} \times 2}{0.1 \times 10^{-3}} = 0.01 \, \text{m} = 1 \, \text{cm} \]
Do đó, khoảng cách giữa các vân sáng hoặc vân tối liên tiếp là 1 cm.
Kết luận
Hiện tượng giao thoa ánh sáng qua khe hẹp cho thấy rõ tính chất sóng của ánh sáng. Thông qua việc quan sát và tính toán các vân giao thoa, chúng ta có thể hiểu thêm về tính chất và hành vi của ánh sáng trong các môi trường khác nhau, cũng như ứng dụng trong các lĩnh vực nghiên cứu khoa học và công nghệ.
Bài tập 7: Tính công suất quang học của một hệ thấu kính
Công suất quang học của một thấu kính hay hệ thấu kính là khả năng hội tụ hoặc phân kỳ của ánh sáng khi nó đi qua thấu kính. Công suất này được đo bằng đi-ốp (dioptre) và được xác định bằng nghịch đảo của tiêu cự của thấu kính. Bài tập này sẽ hướng dẫn cách tính công suất quang học của một hệ thấu kính.
Nguyên lý cơ bản
Công suất quang học \( P \) của một thấu kính được tính theo công thức:
Trong đó:
- \(P\): Công suất quang học (đơn vị: đi-ốp, D).
- \(f\): Tiêu cự của thấu kính (đơn vị: mét).
Đối với hệ hai thấu kính ghép sát nhau, công suất quang học tổng hợp của hệ được tính bằng tổng công suất của từng thấu kính:
Trong đó:
- \(P_{\text{tổng}}\): Công suất quang học tổng hợp của hệ thấu kính.
- \(P_1\): Công suất quang học của thấu kính thứ nhất.
- \(P_2\): Công suất quang học của thấu kính thứ hai.
Các bước thực hiện tính toán
- Xác định tiêu cự của các thấu kính: Đo hoặc biết trước tiêu cự \(f_1\) và \(f_2\) của các thấu kính trong hệ. Tiêu cự có thể dương (thấu kính hội tụ) hoặc âm (thấu kính phân kỳ).
- Tính công suất của từng thấu kính: Sử dụng công thức \(P = \frac{1}{f}\) để tính công suất quang học của từng thấu kính.
- Tính công suất quang học tổng hợp: Cộng công suất của các thấu kính lại với nhau để có công suất tổng hợp của hệ thấu kính.
Ví dụ minh họa
Giả sử chúng ta có hai thấu kính:
- Thấu kính thứ nhất có tiêu cự \(f_1 = 0.2\) m (thấu kính hội tụ).
- Thấu kính thứ hai có tiêu cự \(f_2 = -0.5\) m (thấu kính phân kỳ).
Công suất của thấu kính thứ nhất:
Công suất của thấu kính thứ hai:
Công suất quang học tổng hợp của hệ thấu kính:
Kết luận
Công suất quang học của một hệ thấu kính có thể được tính một cách đơn giản bằng cách cộng các công suất quang học của từng thấu kính trong hệ. Việc tính toán công suất này giúp xác định tính chất hội tụ hoặc phân kỳ của hệ thấu kính, từ đó ứng dụng trong các thiết bị quang học như kính hiển vi, kính thiên văn, và các hệ thống quang học phức tạp khác.
Bài tập 8: Xác định bước sóng ánh sáng qua thí nghiệm nhiễu xạ
Thí nghiệm nhiễu xạ ánh sáng qua khe hẹp là một phương pháp phổ biến để xác định bước sóng của ánh sáng. Hiện tượng nhiễu xạ xảy ra khi ánh sáng đi qua một khe hẹp và tạo ra các vân sáng và vân tối trên màn quan sát, từ đó ta có thể tính toán được bước sóng của ánh sáng sử dụng.
Nguyên lý cơ bản
Khi ánh sáng đi qua một khe hẹp, nó sẽ bị bẻ cong và tạo ra hiện tượng nhiễu xạ, dẫn đến sự hình thành các vân nhiễu xạ trên màn hình. Vị trí của các vân sáng và vân tối có thể được sử dụng để tính toán bước sóng của ánh sáng.
Công thức tính bước sóng của ánh sáng qua thí nghiệm nhiễu xạ được cho bởi:
Trong đó:
- \(\lambda\): Bước sóng của ánh sáng (đơn vị: mét).
- \(d\): Khoảng cách giữa hai khe (đơn vị: mét).
- \(x\): Khoảng cách giữa các vân nhiễu xạ liên tiếp (đơn vị: mét).
- \(L\): Khoảng cách từ khe đến màn quan sát (đơn vị: mét).
- \(m\): Bậc của vân nhiễu xạ (số nguyên: 1, 2, 3,...).
Các bước thực hiện tính toán
- Chuẩn bị dụng cụ: Thiết lập thí nghiệm với nguồn sáng đơn sắc, khe hẹp, và màn quan sát. Đảm bảo khoảng cách giữa khe và màn là \( L \) đã được biết trước.
- Đo khoảng cách giữa các vân sáng liên tiếp: Sử dụng thước đo chính xác để xác định khoảng cách \( x \) giữa các vân sáng hoặc vân tối liên tiếp trên màn quan sát.
- Xác định khoảng cách giữa các khe: Xác định hoặc đo khoảng cách \( d \) giữa hai khe.
- Tính bước sóng ánh sáng: Sử dụng công thức \(\lambda = \frac{d \cdot x}{L \cdot m}\) để tính toán bước sóng của ánh sáng.
Ví dụ minh họa
Giả sử chúng ta có các thông số sau:
- Khoảng cách giữa hai khe \( d = 0.0005 \) m.
- Khoảng cách giữa các vân nhiễu xạ liên tiếp \( x = 0.01 \) m.
- Khoảng cách từ khe đến màn quan sát \( L = 1 \) m.
- Bậc của vân nhiễu xạ \( m = 1 \) (vân sáng bậc 1).
Bước sóng của ánh sáng được tính như sau:
Kết luận
Qua thí nghiệm nhiễu xạ, chúng ta có thể xác định được bước sóng của ánh sáng một cách chính xác. Việc này không chỉ giúp hiểu rõ hơn về tính chất của ánh sáng mà còn ứng dụng trong nhiều lĩnh vực khoa học và công nghệ, như trong quang học lượng tử, truyền thông và các nghiên cứu về vật liệu.

Bài tập 9: Tính khoảng cách giữa hai vạch sáng trong thí nghiệm Young
Thí nghiệm Young là một thí nghiệm quan trọng trong quang học, được sử dụng để chứng minh tính chất sóng của ánh sáng và xác định khoảng cách giữa các vạch sáng tạo ra trên màn hình. Thí nghiệm này dựa trên hiện tượng giao thoa ánh sáng khi ánh sáng đi qua hai khe hẹp.
Nguyên lý cơ bản
Khi ánh sáng từ một nguồn đơn sắc đi qua hai khe hẹp, nó sẽ tạo ra hai chùm sáng, sau đó giao thoa với nhau. Sự giao thoa này tạo ra các vân sáng (nơi hai sóng tăng cường lẫn nhau) và các vân tối (nơi hai sóng triệt tiêu lẫn nhau) trên màn quan sát.
Công thức để tính khoảng cách \( \Delta y \) giữa hai vạch sáng liên tiếp trên màn hình là:
Trong đó:
- \(\lambda\): Bước sóng của ánh sáng (đơn vị: mét).
- \(L\): Khoảng cách từ hai khe đến màn quan sát (đơn vị: mét).
- \(d\): Khoảng cách giữa hai khe (đơn vị: mét).
- \(\Delta y\): Khoảng cách giữa hai vạch sáng liên tiếp (đơn vị: mét).
Các bước thực hiện tính toán
- Chuẩn bị dụng cụ: Thiết lập thí nghiệm với nguồn sáng đơn sắc (như đèn laser), hai khe hẹp cách nhau một khoảng \( d \), và màn quan sát đặt cách khe một khoảng \( L \).
- Xác định các thông số cần thiết: Đo khoảng cách \( L \) từ khe đến màn, đo khoảng cách \( d \) giữa hai khe, và biết trước bước sóng \( \lambda \) của nguồn sáng sử dụng.
- Tính khoảng cách giữa hai vạch sáng: Sử dụng công thức \(\Delta y = \frac{\lambda \cdot L}{d}\) để tính toán khoảng cách giữa hai vạch sáng liên tiếp trên màn quan sát.
Ví dụ minh họa
Giả sử chúng ta có các thông số sau:
- Bước sóng của ánh sáng sử dụng \( \lambda = 600 \) nm (nanomet).
- Khoảng cách từ hai khe đến màn \( L = 1.5 \) m.
- Khoảng cách giữa hai khe \( d = 0.0001 \) m.
Khoảng cách giữa hai vạch sáng liên tiếp được tính như sau:
Kết luận
Thí nghiệm Young giúp chúng ta xác định được khoảng cách giữa các vạch sáng, qua đó chứng minh được tính chất sóng của ánh sáng. Việc hiểu rõ về hiện tượng giao thoa không chỉ có ý nghĩa trong lý thuyết mà còn ứng dụng thực tiễn trong các lĩnh vực như đo lường chính xác và quang học hiện đại.
Bài tập 10: Phân tích và giải thích hiện tượng phân cực ánh sáng
Hiện tượng phân cực ánh sáng là một hiện tượng quan trọng trong quang học, xảy ra khi ánh sáng chỉ dao động theo một hướng nhất định. Phân cực ánh sáng có thể được quan sát và phân tích thông qua các thí nghiệm và dụng cụ quang học như kính phân cực.
Nguyên lý cơ bản
Ánh sáng thông thường là sóng điện từ dao động theo nhiều hướng khác nhau. Khi ánh sáng đi qua một bộ lọc phân cực, các sóng ánh sáng dao động theo hướng phân cực của bộ lọc sẽ được truyền qua, trong khi các sóng dao động theo các hướng khác sẽ bị loại bỏ. Kết quả là ánh sáng sau khi qua bộ lọc phân cực sẽ dao động theo một hướng duy nhất.
Công thức và các yếu tố liên quan
Hiện tượng phân cực có thể được mô tả bằng công thức liên quan đến cường độ ánh sáng:
Trong đó:
- \(I\): Cường độ ánh sáng sau khi qua bộ lọc phân cực.
- \(I_0\): Cường độ ánh sáng trước khi qua bộ lọc phân cực.
- \(\theta\): Góc giữa hướng phân cực của ánh sáng và hướng phân cực của bộ lọc.
Các bước thực hiện thí nghiệm phân cực ánh sáng
- Chuẩn bị dụng cụ: Sử dụng một nguồn sáng đơn sắc, một bộ lọc phân cực, và một màn quan sát hoặc cảm biến để đo cường độ ánh sáng.
- Đặt bộ lọc phân cực: Đặt bộ lọc phân cực giữa nguồn sáng và màn quan sát sao cho hướng phân cực của bộ lọc có thể được điều chỉnh.
- Đo cường độ ánh sáng: Đo cường độ ánh sáng \( I_0 \) khi bộ lọc phân cực không được sử dụng, và sau đó đo cường độ ánh sáng \( I \) khi ánh sáng đi qua bộ lọc phân cực tại các góc khác nhau.
- Phân tích dữ liệu: Sử dụng công thức \( I = I_0 \cdot \cos^2(\theta) \) để phân tích mối quan hệ giữa cường độ ánh sáng và góc phân cực. Xác định góc phân cực tại điểm cường độ ánh sáng đạt cực đại hoặc cực tiểu.
Ví dụ minh họa
Giả sử ánh sáng có cường độ ban đầu \( I_0 = 100 \) lux và bộ lọc phân cực được đặt tại góc \( \theta = 30^\circ \). Tính cường độ ánh sáng sau khi qua bộ lọc phân cực:
Kết luận
Hiện tượng phân cực ánh sáng không chỉ chứng minh tính chất sóng của ánh sáng mà còn có ứng dụng rộng rãi trong các thiết bị quang học, như kính phân cực, màn hình LCD và các công nghệ khác. Việc hiểu và phân tích hiện tượng này giúp chúng ta hiểu rõ hơn về hành vi của ánh sáng và ứng dụng trong khoa học và công nghệ.