Chủ đề vật kính của kính hiển vi có đặc điểm: Vật kính của kính hiển vi có vai trò quan trọng trong việc phóng đại hình ảnh, giúp quan sát các chi tiết nhỏ mà mắt thường không thể thấy. Bài viết này sẽ giới thiệu chi tiết về đặc điểm, cấu tạo, và ứng dụng của vật kính trong các lĩnh vực khoa học và đời sống.
Mục lục
- Đặc Điểm Của Vật Kính Trong Kính Hiển Vi
- Mục Lục Tổng Hợp
- 10 Dạng Bài Tập Vật Lý Về Kính Hiển Vi
- Bài Tập 1: Tính Độ Phóng Đại Của Hệ Thống Kính Hiển Vi
- Bài Tập 2: Tính Độ Phân Giải Của Vật Kính Trong Kính Hiển Vi
- Bài Tập 3: Xác Định Khoảng Cách Làm Việc Của Vật Kính
- Bài Tập 4: Phân Loại Các Loại Vật Kính Dựa Trên Độ Phóng Đại
- Bài Tập 5: Tính Độ Phóng Đại Tổng Hợp Của Kính Hiển Vi
- Bài Tập 6: So Sánh Độ Phân Giải Giữa Các Loại Vật Kính
- Bài Tập 7: Tính Toán Sự Khác Biệt Khi Sử Dụng Các Vật Kính Khác Nhau
- Bài Tập 8: Tìm Hiểu Ứng Dụng Thực Tiễn Của Vật Kính Trong Y Học
- Bài Tập 9: Đánh Giá Chất Lượng Hình Ảnh Dựa Trên Độ Phân Giải
- Bài Tập 10: Phân Tích Tác Động Của Khoảng Cách Làm Việc Đến Hình Ảnh
Đặc Điểm Của Vật Kính Trong Kính Hiển Vi
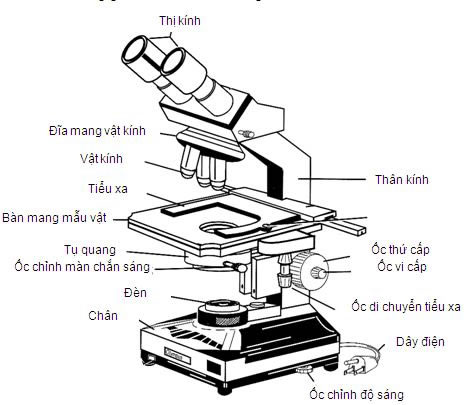
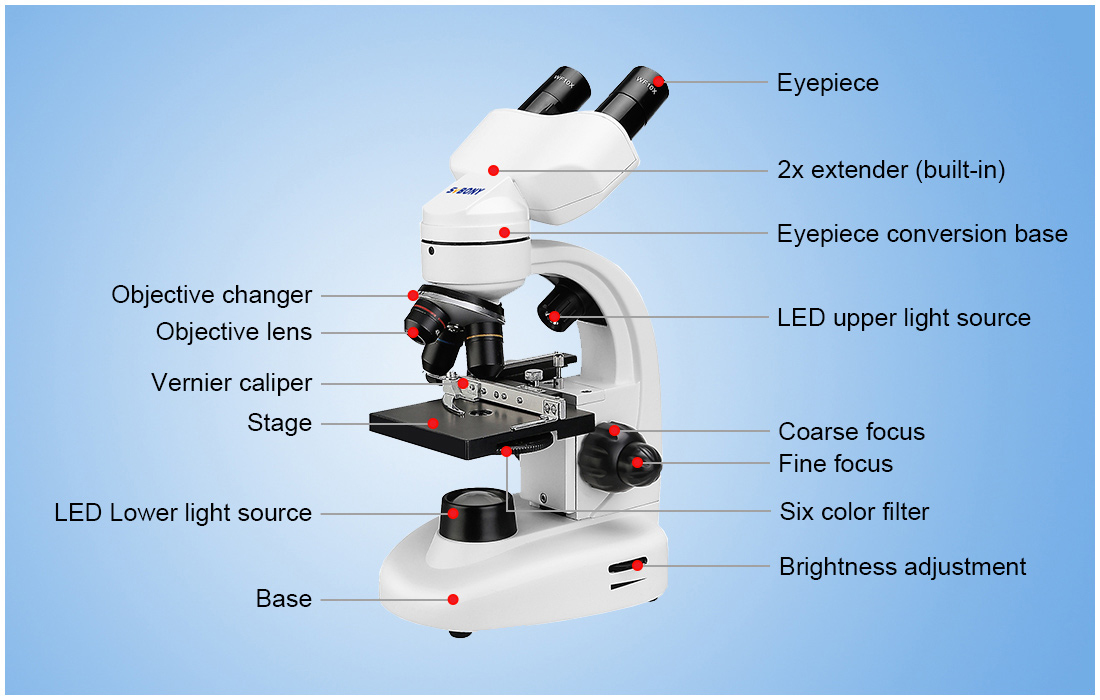
Vật kính là một trong những bộ phận quan trọng nhất của kính hiển vi, giúp phóng đại hình ảnh của vật mẫu để quan sát các chi tiết nhỏ mà mắt thường không thể nhìn thấy. Dưới đây là các đặc điểm chính của vật kính:
1. Cấu Tạo Và Chất Liệu Của Vật Kính
- Vật kính được chế tạo từ các loại thủy tinh quang học chất lượng cao hoặc vật liệu đặc biệt để đảm bảo độ trong suốt và khả năng phóng đại.
- Thường bao gồm nhiều thấu kính lồi ghép lại với nhau để tạo ra hình ảnh rõ nét và có độ phóng đại lớn.
2. Khả Năng Phóng Đại
Vật kính thường có độ phóng đại dao động từ 4x đến 100x, tùy thuộc vào loại kính hiển vi. Khi kết hợp với thị kính, độ phóng đại tổng có thể lên tới hàng nghìn lần, giúp quan sát chi tiết cấu trúc tế bào, vi sinh vật và các vật liệu nhỏ khác.
3. Độ Phân Giải
Độ phân giải của vật kính rất cao, giúp phân biệt các chi tiết nhỏ gần nhau. Điều này rất quan trọng trong nghiên cứu sinh học và y học, nơi cần quan sát chi tiết các cấu trúc tế bào và mô.
4. Khoảng Cách Làm Việc
Khoảng cách làm việc của vật kính là khoảng cách giữa vật kính và vật mẫu khi hình ảnh được lấy nét. Các vật kính có độ phóng đại cao thường có khoảng cách làm việc ngắn hơn.
5. Ứng Dụng Của Vật Kính
- Sử dụng rộng rãi trong nghiên cứu sinh học để quan sát tế bào, vi khuẩn và các cấu trúc siêu nhỏ.
- Trong y học, vật kính giúp phân tích mô bệnh học và chẩn đoán bệnh.
- Được ứng dụng trong công nghệ vật liệu để nghiên cứu các vật liệu mới và kiểm tra chất lượng sản phẩm.
6. Công Thức Tính Số Phóng Đại
Độ phóng đại của kính hiển vi có thể được tính theo công thức:
Trong đó:
- \(M\) là độ phóng đại tổng.
- \(L\) là độ dài quang học của kính hiển vi.
- \(f_1\) và \(f_2\) lần lượt là tiêu cự của vật kính và thị kính.
- \(D\) là khoảng cách cực cận của mắt.

.png)
Mục Lục Tổng Hợp
1. Giới thiệu về vật kính trong kính hiển vi
Vật kính là một thành phần quan trọng trong kính hiển vi, đóng vai trò quyết định chất lượng hình ảnh và độ phóng đại.
2. Cấu tạo và phân loại vật kính
Vật kính có nhiều loại khác nhau dựa trên độ phóng đại và ứng dụng, mỗi loại có cấu tạo và đặc điểm riêng.
3. Nguyên lý hoạt động của vật kính trong kính hiển vi
Nguyên lý hoạt động của vật kính dựa trên sự hội tụ ánh sáng để tạo ra hình ảnh phóng đại rõ nét.
4. Ứng dụng của vật kính trong các lĩnh vực khoa học
Vật kính được sử dụng rộng rãi trong y học, sinh học, và nghiên cứu khoa học.
5. Các yếu tố ảnh hưởng đến chất lượng hình ảnh của vật kính
Các yếu tố như độ phóng đại, độ phân giải, và chất lượng thấu kính ảnh hưởng trực tiếp đến hình ảnh.
6. Cách sử dụng và bảo quản vật kính
Hướng dẫn cách sử dụng và bảo quản vật kính đúng cách để đảm bảo hiệu suất và tuổi thọ lâu dài.
7. Những tiến bộ và phát triển trong công nghệ vật kính
Các công nghệ mới giúp cải thiện chất lượng và tính năng của vật kính.
10 Dạng Bài Tập Vật Lý Về Kính Hiển Vi
-
Bài tập 1: Tính độ phóng đại của kính hiển vi
Cho biết tiêu cự của vật kính và thị kính, tính độ phóng đại tổng thể của kính hiển vi.
Lời giải: Sử dụng công thức: \[ M = \dfrac{f_1 \times D}{f_2 \times O} \], trong đó \( f_1 \) là tiêu cự vật kính, \( f_2 \) là tiêu cự thị kính, \( D \) là khoảng cách ngắm chừng, và \( O \) là khoảng cách từ vật đến vật kính.
-
Bài tập 2: Xác định khoảng cách giữa vật và vật kính
Với độ phóng đại và tiêu cự đã cho, tính khoảng cách giữa vật và vật kính.
Lời giải: Áp dụng công thức: \[ O = \dfrac{f_1 \times M}{D} \]
-
Bài tập 3: Tính độ phân giải của kính hiển vi
Dựa vào bước sóng ánh sáng và khẩu độ, tính độ phân giải của kính hiển vi.
Lời giải: Sử dụng công thức: \[ d = \dfrac{\lambda}{2NA} \], trong đó \( \lambda \) là bước sóng ánh sáng, \( NA \) là khẩu độ số của vật kính.
-
Bài tập 4: Xác định tiêu cự của vật kính
Dùng dữ kiện về độ phóng đại và khoảng cách để tìm tiêu cự của vật kính.
Lời giải: Công thức liên hệ: \[ f_1 = \dfrac{O \times M}{D} \]
-
Bài tập 5: Tính độ phóng đại cần thiết để quan sát chi tiết nhỏ nhất
Với độ phân giải và chi tiết nhỏ nhất đã biết, tính độ phóng đại cần thiết.
Lời giải: Sử dụng công thức: \[ M = \dfrac{D}{d} \], trong đó \( d \) là kích thước chi tiết nhỏ nhất cần quan sát.
-
Bài tập 6: Xác định khoảng cách ngắm chừng
Với độ phóng đại và tiêu cự thị kính, tính khoảng cách ngắm chừng.
Lời giải: Sử dụng công thức: \[ D = \dfrac{f_2 \times M}{f_1} \]
-
Bài tập 7: Tính khẩu độ số của vật kính
Với tiêu cự và đường kính khẩu độ đã biết, tính khẩu độ số của vật kính.
Lời giải: Công thức: \[ NA = n \times \sin(\theta) \], trong đó \( n \) là chiết suất của môi trường và \( \theta \) là góc bán khẩu độ.
-
Bài tập 8: Xác định bước sóng ánh sáng sử dụng
Dùng dữ liệu về độ phân giải và khẩu độ số, tính bước sóng ánh sáng cần dùng.
Lời giải: Sử dụng công thức: \[ \lambda = 2NA \times d \]
-
Bài tập 9: Xác định vùng quan sát qua kính hiển vi
Tính toán kích thước vùng quan sát dựa trên độ phóng đại và thị kính.
Lời giải: Công thức: \[ \text{Vùng quan sát} = \dfrac{\text{Kích thước trường thị kính}}{M} \]
-
Bài tập 10: Tính chiều dài của mẫu vật quan sát qua kính hiển vi
Với độ phóng đại và kích thước trên hình ảnh, tính chiều dài thật của mẫu vật.
Lời giải: Sử dụng công thức: \[ L = \dfrac{l_{\text{ảnh}}}{M} \], trong đó \( l_{\text{ảnh}} \) là chiều dài trên ảnh.

Bài Tập 1: Tính Độ Phóng Đại Của Hệ Thống Kính Hiển Vi
Trong bài tập này, chúng ta sẽ tính độ phóng đại của hệ thống kính hiển vi dựa trên các thông số đã biết của vật kính và thị kính. Độ phóng đại của kính hiển vi được tính bằng tích của độ phóng đại vật kính và thị kính.
Thông số bài toán
- Tiêu cự vật kính: \( f_1 \) (mm)
- Tiêu cự thị kính: \( f_2 \) (mm)
- Khoảng cách giữa vật kính và thị kính: \( L \) (mm)
Bước 1: Tính độ phóng đại của vật kính
Độ phóng đại của vật kính được xác định bằng công thức:
\[ M_1 = \dfrac{L}{f_1} \]
Bước 2: Tính độ phóng đại của thị kính
Độ phóng đại của thị kính được xác định bằng công thức:
\[ M_2 = \dfrac{D}{f_2} \]
Trong đó, \( D \) là khoảng cách ngắm chừng thông thường (250 mm).
Bước 3: Tính độ phóng đại tổng thể của hệ thống kính hiển vi
Độ phóng đại tổng thể của hệ thống kính hiển vi là:
\[ M = M_1 \times M_2 = \dfrac{L}{f_1} \times \dfrac{D}{f_2} \]
Kết quả
Với các giá trị đã cho, chúng ta có thể tính toán độ phóng đại tổng thể của hệ thống kính hiển vi theo công thức trên. Đảm bảo rằng các đơn vị đo lường phù hợp để có kết quả chính xác.

XEM THÊM:
Bài Tập 2: Tính Độ Phân Giải Của Vật Kính Trong Kính Hiển Vi
Bài tập này hướng dẫn cách tính độ phân giải của vật kính trong kính hiển vi, một yếu tố quan trọng để đánh giá khả năng quan sát chi tiết của mẫu vật. Độ phân giải phụ thuộc vào bước sóng ánh sáng và khẩu độ số của vật kính.
Thông số bài toán
- Bước sóng ánh sáng sử dụng: \(\lambda\) (nm)
- Khẩu độ số của vật kính: \(NA\)
Bước 1: Xác định công thức tính độ phân giải
Độ phân giải \(d\) được tính theo công thức:
\[ d = \dfrac{\lambda}{2 \times NA} \]
Bước 2: Tính toán độ phân giải
Thay các giá trị cụ thể của \(\lambda\) và \(NA\) vào công thức trên để tính toán độ phân giải \(d\). Giá trị \(d\) càng nhỏ, độ phân giải càng cao, cho phép quan sát được các chi tiết nhỏ hơn.
Kết quả
Sau khi tính toán, bạn sẽ có kết quả độ phân giải của vật kính. Điều này giúp xác định khả năng của kính hiển vi trong việc phân biệt các chi tiết nhỏ trong mẫu vật.

Bài Tập 3: Xác Định Khoảng Cách Làm Việc Của Vật Kính
Khoảng cách làm việc của vật kính trong kính hiển vi là một yếu tố quan trọng để đạt được hình ảnh rõ nét và chính xác. Để xác định khoảng cách này, chúng ta cần tính toán dựa trên một số yếu tố quan trọng như độ phóng đại của vật kính, kích thước mẫu và tiêu cự của hệ thống quang học.
Bước 1: Xác định độ phóng đại của vật kính.
- Ví dụ: Vật kính có độ phóng đại 10x, 40x, hoặc 100x.
Bước 2: Tính khoảng cách làm việc dựa trên công thức:
\[
d = \frac{f}{{n \cdot \sin \theta}}
\]
Trong đó:
- d: Khoảng cách làm việc (mm)
- f: Tiêu cự của vật kính (mm)
- n: Chỉ số khúc xạ của môi trường giữa vật kính và mẫu
- \(\theta\): Góc tới của ánh sáng (độ)
Bước 3: Đặt tiêu cự của vật kính và tính toán để xác định khoảng cách làm việc.
Ví dụ: Với vật kính có tiêu cự f = 4 mm và chỉ số khúc xạ n = 1,0 (không khí), nếu góc tới \(\theta = 60^\circ\), ta tính được:
\[
d = \frac{4}{{1,0 \cdot \sin 60^\circ}} \approx 4,62 \, \text{mm}
\]
Bước 4: Kiểm tra và điều chỉnh khoảng cách làm việc để đạt được hình ảnh rõ ràng nhất.
Quá trình này đòi hỏi sự tinh chỉnh chính xác của hệ thống quang học, giúp đảm bảo độ phân giải và chi tiết của hình ảnh quan sát được tối ưu.
Bài Tập 4: Phân Loại Các Loại Vật Kính Dựa Trên Độ Phóng Đại
Vật kính của kính hiển vi có thể được phân loại dựa trên độ phóng đại của chúng. Việc hiểu rõ về các loại vật kính này giúp người sử dụng lựa chọn chính xác công cụ phù hợp với nhu cầu nghiên cứu của mình. Sau đây là một số loại vật kính phổ biến dựa trên độ phóng đại:
- Vật kính thấp (Low Power Objective): Độ phóng đại từ \(4x\) đến \(10x\). Loại này thường được sử dụng để quan sát các mẫu lớn, giúp định vị mẫu dễ dàng.
- Vật kính trung bình (Medium Power Objective): Độ phóng đại từ \(20x\) đến \(40x\). Đây là loại vật kính tiêu chuẩn cho việc quan sát chi tiết hơn.
- Vật kính cao (High Power Objective): Độ phóng đại từ \(60x\) đến \(100x\). Được sử dụng để quan sát chi tiết nhỏ hơn trong cấu trúc của mẫu vật.
- Vật kính dầu (Oil Immersion Objective): Độ phóng đại từ \(100x\) trở lên. Loại vật kính này yêu cầu sử dụng dầu để tăng cường độ phân giải của hình ảnh.
Để phân loại đúng, ta cần biết độ phóng đại tương ứng với mỗi loại vật kính, từ đó áp dụng trong các nghiên cứu và thí nghiệm cụ thể.

Bài Tập 5: Tính Độ Phóng Đại Tổng Hợp Của Kính Hiển Vi
Để tính độ phóng đại tổng hợp của kính hiển vi, ta cần thực hiện các bước sau:
- Xác định độ phóng đại của vật kính (\(M_v\)):
- Độ phóng đại của vật kính là tỉ số giữa kích thước của ảnh tạo bởi vật kính với kích thước của vật thật.
- \(M_v = \frac{\text{kích thước ảnh}}{\text{kích thước vật thật}}\)
- Thông thường, các vật kính sẽ có độ phóng đại cố định như \(4x\), \(10x\), \(40x\), hoặc \(100x\).
- Xác định độ phóng đại của thị kính (\(M_t\)):
- Độ phóng đại của thị kính là tỉ số giữa kích thước của ảnh cuối cùng (mắt người nhìn thấy) với kích thước của ảnh từ vật kính.
- \(M_t = \frac{\text{kích thước ảnh cuối cùng}}{\text{kích thước ảnh từ vật kính}}\)
- Thị kính cũng có các độ phóng đại phổ biến như \(10x\) hoặc \(15x\).
- Tính độ phóng đại tổng hợp (\(M_{total}\)):
- Độ phóng đại tổng hợp là tích của độ phóng đại của vật kính và thị kính.
- \(M_{total} = M_v \times M_t\)
- Ví dụ: Nếu \(M_v = 40x\) và \(M_t = 10x\), thì độ phóng đại tổng hợp sẽ là:
- \[M_{total} = 40 \times 10 = 400x\]
Với các bước trên, ta có thể dễ dàng tính toán và so sánh độ phóng đại của các hệ thống kính hiển vi khác nhau. Điều này giúp tối ưu hóa việc lựa chọn kính hiển vi phù hợp cho từng nhu cầu sử dụng cụ thể.

Bài Tập 6: So Sánh Độ Phân Giải Giữa Các Loại Vật Kính
Trong bài tập này, chúng ta sẽ so sánh độ phân giải giữa các loại vật kính của kính hiển vi quang học. Độ phân giải của vật kính là khả năng phân biệt hai điểm gần nhau thành hai điểm riêng biệt trên mẫu vật quan sát.
Để hiểu rõ hơn, chúng ta cần xét đến các yếu tố ảnh hưởng đến độ phân giải như sau:
- Độ mở số (Numerical Aperture - NA): Là thông số quan trọng quyết định độ phân giải của vật kính. Vật kính có độ mở số càng cao thì khả năng thu nhận ánh sáng từ mẫu vật càng tốt, dẫn đến độ phân giải càng cao.
- Độ phóng đại: Độ phóng đại càng lớn không đồng nghĩa với việc độ phân giải càng cao. Chỉ số NA cùng với bước sóng ánh sáng mới là yếu tố quyết định độ phân giải thực tế.
- Bước sóng ánh sáng: Độ phân giải tối đa được tính theo công thức của Abbe:
\[
d = \frac{\lambda}{2 \times NA}
\]
Trong đó:
- \(d\): Độ phân giải tối thiểu (khoảng cách nhỏ nhất giữa hai điểm còn được phân biệt).
- \(\lambda\): Bước sóng ánh sáng sử dụng trong quan sát.
- \(NA\): Độ mở số của vật kính.
Bây giờ, hãy so sánh độ phân giải của hai loại vật kính với các thông số như sau:
| Loại Vật Kính | Độ Mở Số (NA) | Bước Sóng Ánh Sáng (\(\lambda\)) | Độ Phân Giải (d) |
|---|---|---|---|
| Vật kính A | 1.25 | 550 nm | \[ d_A = \frac{550 \text{ nm}}{2 \times 1.25} \approx 220 \text{ nm} \] |
| Vật kính B | 0.95 | 550 nm | \[ d_B = \frac{550 \text{ nm}}{2 \times 0.95} \approx 289 \text{ nm} \] |
Như vậy, từ bảng so sánh trên, ta có thể thấy rằng vật kính A với độ mở số cao hơn có độ phân giải tốt hơn so với vật kính B. Điều này chứng tỏ rằng việc lựa chọn vật kính có độ mở số lớn là cực kỳ quan trọng trong việc quan sát các chi tiết nhỏ và rõ nét trên mẫu vật.
Bài Tập 7: Tính Toán Sự Khác Biệt Khi Sử Dụng Các Vật Kính Khác Nhau
Trong bài tập này, chúng ta sẽ tìm hiểu cách tính toán sự khác biệt khi sử dụng các loại vật kính khác nhau trong kính hiển vi. Việc này giúp chúng ta hiểu rõ hơn về ảnh hưởng của từng loại vật kính đến chất lượng hình ảnh và khả năng quan sát.
- Đặt Vấn Đề: Tính toán sự khác biệt giữa hai loại vật kính với độ phóng đại khác nhau. Ví dụ, so sánh vật kính 10x với vật kính 40x.
-
Thông Tin Cần Thiết:
- Độ phóng đại của vật kính (M)
- Độ phân giải của vật kính (R)
- Kích thước của tiêu điểm (D)
-
Công Thức Tính Độ Phóng Đại Tổng Hợp:
Độ phóng đại tổng hợp của kính hiển vi được tính bằng tích của độ phóng đại của vật kính và độ phóng đại của thị kính. Công thức là:
\[ M_{total} = M_{object} \times M_{eyepiece} \]
-
Công Thức Tính Độ Phân Giải:
Độ phân giải của vật kính có thể tính bằng công thức:
\[ R = \frac{0.61 \lambda}{NA} \]
Trong đó:
- \(\lambda\) là bước sóng của ánh sáng sử dụng.
- NA là số khẩu độ của vật kính.
-
Ví Dụ Tính Toán:
Loại Vật Kính Độ Phóng Đại Độ Phân Giải Vật Kính 10x 10x \(\frac{0.61 \lambda}{NA_{10}}\) Vật Kính 40x 40x \(\frac{0.61 \lambda}{NA_{40}}\) -
So Sánh:
Sử dụng các giá trị tính được để so sánh sự khác biệt trong độ phân giải và độ phóng đại giữa các vật kính. Điều này giúp xác định loại vật kính nào phù hợp hơn cho mục đích quan sát cụ thể.

Bài Tập 8: Tìm Hiểu Ứng Dụng Thực Tiễn Của Vật Kính Trong Y Học
Vật kính trong kính hiển vi đóng vai trò quan trọng trong việc nghiên cứu và chẩn đoán trong y học. Các vật kính với các đặc điểm khác nhau có thể được áp dụng để quan sát và phân tích các mẫu sinh học, giúp cải thiện khả năng chẩn đoán và điều trị bệnh. Dưới đây là các ứng dụng thực tiễn của vật kính trong y học.
-
Quan Sát Mẫu Sinh Học:
Vật kính có độ phóng đại cao như 40x hoặc 100x được sử dụng để quan sát các mẫu mô và tế bào. Điều này cho phép bác sĩ và nhà nghiên cứu nhìn thấy các chi tiết nhỏ của tế bào và mô, hỗ trợ trong việc chẩn đoán bệnh lý như ung thư, viêm nhiễm, và các bệnh di truyền.
-
Phân Tích Tế Bào:
Vật kính với khả năng phân giải cao giúp phân tích các đặc điểm của tế bào, bao gồm kích thước, hình dạng, và cấu trúc nội bào. Điều này rất quan trọng trong nghiên cứu bệnh lý tế bào và phát triển các phương pháp điều trị mới.
-
Nghiên Cứu Tinh Thể Sinh Học:
Các vật kính chuyên dụng cho quan sát tinh thể sinh học giúp nghiên cứu cấu trúc của protein và axit nucleic. Điều này hỗ trợ trong việc hiểu biết về cấu trúc và chức năng của các phân tử sinh học, và thiết kế thuốc nhắm mục tiêu.
-
Chẩn Đoán Bệnh Nhiễm Khuẩn:
Vật kính với khả năng phân giải tốt giúp phát hiện và phân tích các vi sinh vật gây bệnh như vi khuẩn, virus và nấm trong mẫu bệnh phẩm. Điều này là thiết yếu để chẩn đoán chính xác các bệnh nhiễm khuẩn và hướng dẫn điều trị hiệu quả.
-
Phát Hiện Tế Bào Bất Thường:
Vật kính có độ phóng đại cao giúp phát hiện các tế bào bất thường hoặc tế bào ung thư trong mẫu sinh thiết. Điều này rất quan trọng trong việc phát hiện sớm bệnh ung thư và theo dõi sự tiến triển của bệnh.
Vật kính không chỉ đóng vai trò quan trọng trong nghiên cứu y học mà còn trong việc cải thiện chất lượng chăm sóc sức khỏe và phát triển các phương pháp điều trị mới. Hiểu biết về các ứng dụng thực tiễn của vật kính giúp nâng cao hiệu quả trong chẩn đoán và điều trị bệnh.
Bài Tập 9: Đánh Giá Chất Lượng Hình Ảnh Dựa Trên Độ Phân Giải
Đánh giá chất lượng hình ảnh của kính hiển vi là một yếu tố quan trọng để đảm bảo rằng các hình ảnh quan sát được rõ ràng và chi tiết. Độ phân giải của vật kính ảnh hưởng trực tiếp đến khả năng phân biệt các chi tiết nhỏ trong mẫu. Dưới đây là các bước để đánh giá chất lượng hình ảnh dựa trên độ phân giải:
-
Xác Định Độ Phân Giải:
Độ phân giải của vật kính được tính bằng công thức:
\[ R = \frac{0.61 \lambda}{NA} \]
Trong đó:
- \(\lambda\) là bước sóng của ánh sáng sử dụng.
- NA là số khẩu độ của vật kính.
-
Đo Độ Phân Giải:
Sử dụng một mẫu chuẩn với các chi tiết nhỏ biết trước để đo độ phân giải của vật kính. So sánh các chi tiết quan sát được với kích thước thực tế để đánh giá độ phân giải.
-
So Sánh Các Vật Kính:
Loại Vật Kính Bước Sóng (λ) Số Khẩu Độ (NA) Độ Phân Giải (R) Vật Kính 10x 550 nm 0.25 \(\frac{0.61 \times 550}{0.25}\) = 1334 nm Vật Kính 40x 550 nm 0.65 \(\frac{0.61 \times 550}{0.65}\) = 518 nm -
Đánh Giá Chất Lượng Hình Ảnh:
Sử dụng các kết quả đo được để đánh giá chất lượng hình ảnh. Vật kính với độ phân giải cao hơn sẽ cung cấp hình ảnh rõ ràng hơn và khả năng phân biệt các chi tiết nhỏ tốt hơn.
-
Cải Thiện Độ Phân Giải:
Để cải thiện độ phân giải và chất lượng hình ảnh, có thể sử dụng vật kính với số khẩu độ cao hơn hoặc bước sóng ánh sáng ngắn hơn. Điều này giúp tăng khả năng phân biệt chi tiết và cải thiện chất lượng hình ảnh quan sát được.
Đánh giá chất lượng hình ảnh dựa trên độ phân giải là một bước quan trọng để đảm bảo sự chính xác và độ rõ ràng trong quan sát kính hiển vi. Việc hiểu rõ các yếu tố ảnh hưởng đến độ phân giải giúp cải thiện chất lượng hình ảnh và hiệu quả trong nghiên cứu và chẩn đoán.
Bài Tập 10: Phân Tích Tác Động Của Khoảng Cách Làm Việc Đến Hình Ảnh
Khoảng cách làm việc (working distance) là khoảng cách từ mặt dưới của vật kính đến mặt của mẫu khi vật kính ở trong trạng thái lấy nét. Khoảng cách làm việc ảnh hưởng lớn đến chất lượng hình ảnh quan sát được trong kính hiển vi. Dưới đây là phân tích tác động của khoảng cách làm việc đến hình ảnh:
-
Hiệu Ứng Đến Độ Phóng Đại:
Khi khoảng cách làm việc giảm, vật kính có thể phóng đại hình ảnh của mẫu một cách chính xác hơn. Tuy nhiên, khoảng cách làm việc quá nhỏ có thể dẫn đến hiện tượng va chạm với mẫu hoặc gây khó khăn trong việc điều chỉnh.
-
Tác Động Đến Độ Sáng:
Khi khoảng cách làm việc tăng, lượng ánh sáng thu vào qua vật kính giảm, điều này có thể làm giảm độ sáng của hình ảnh. Do đó, việc chọn vật kính với khoảng cách làm việc phù hợp giúp duy trì độ sáng cần thiết cho quan sát rõ ràng.
-
Ảnh Hưởng Đến Độ Phân Giải:
Khoảng cách làm việc ảnh hưởng đến độ phân giải của vật kính. Vật kính có khoảng cách làm việc ngắn thường có độ phân giải cao hơn, cho phép phân biệt các chi tiết nhỏ hơn trong mẫu. Ngược lại, vật kính có khoảng cách làm việc dài thường có độ phân giải thấp hơn.
-
Khả Năng Quan Sát Mẫu:
Khoảng cách làm việc dài cho phép quan sát các mẫu dày hơn hoặc các mẫu được chuẩn bị với các lớp dày. Điều này là quan trọng trong việc nghiên cứu các mẫu sinh học hoặc mẫu vật liệu có độ dày khác nhau.
-
Điều Chỉnh Khoảng Cách Làm Việc:
Để tối ưu hóa chất lượng hình ảnh, cần điều chỉnh khoảng cách làm việc sao cho vật kính và mẫu có khoảng cách phù hợp. Điều này có thể yêu cầu thay đổi vật kính hoặc sử dụng các thiết bị hỗ trợ điều chỉnh khoảng cách làm việc.
Khoảng cách làm việc là một yếu tố quan trọng trong việc tối ưu hóa chất lượng hình ảnh trong kính hiển vi. Hiểu và điều chỉnh đúng khoảng cách làm việc giúp cải thiện khả năng quan sát và phân tích mẫu một cách hiệu quả.