Chủ đề mắt và dụng cụ quang học: Mắt và dụng cụ quang học là chủ đề quan trọng giúp chúng ta hiểu rõ hơn về cách mắt hoạt động và các thiết bị hỗ trợ thị giác. Bài viết này sẽ cung cấp cho bạn kiến thức toàn diện về cấu tạo của mắt, các tật khúc xạ thường gặp và vai trò của các dụng cụ quang học trong việc cải thiện khả năng nhìn.
Mục lục
- Mắt và Dụng Cụ Quang Học
- Mục Lục Tổng Hợp Về Mắt và Dụng Cụ Quang Học
- 10 Dạng Bài Tập Toán Lý Về Mắt và Dụng Cụ Quang Học
- Bài Tập 1: Tính Toán Tiêu Cự Của Thấu Kính Mỏng
- Bài Tập 2: Xác Định Số Bội Giác Của Kính Lúp
- Bài Tập 3: Giải Bài Toán Về Kính Hiển Vi
- Bài Tập 4: Tính Số Bội Giác Của Kính Thiên Văn
- Bài Tập 5: Ứng Dụng Công Thức Thấu Kính Mỏng Trong Các Bài Toán
- Bài Tập 6: Phân Tích Hình Ảnh Tạo Bởi Kính Lúp
- Bài Tập 7: Giải Các Bài Toán Liên Quan Đến Tật Khúc Xạ Của Mắt
- Bài Tập 8: Giải Bài Toán Về Hệ Thấu Kính Đồng Trục
- Bài Tập 9: Tính Toán Liên Quan Đến Kính Viễn Và Kính Cận
- Bài Tập 10: Bài Tập Tổng Hợp Về Quang Học Liên Quan Đến Mắt
Mắt và Dụng Cụ Quang Học
Mắt là một cơ quan quan trọng giúp chúng ta nhận biết được hình ảnh từ môi trường xung quanh. Quá trình nhìn được diễn ra khi ánh sáng từ vật thể đi qua các phần tử quang học của mắt và tạo thành ảnh trên võng mạc. Tuy nhiên, mắt có thể gặp phải một số tật khúc xạ như cận thị, viễn thị, và loạn thị, gây khó khăn trong việc nhìn rõ. Các dụng cụ quang học như kính lúp, kính hiển vi, kính thiên văn, và kính mắt đóng vai trò hỗ trợ cải thiện khả năng nhìn của mắt.
1. Cấu Tạo và Chức Năng Của Mắt
- Giác mạc: Bề mặt trong suốt phía trước của mắt, cho phép ánh sáng đi vào và giúp tập trung ánh sáng.
- Thủy tinh thể: Thấu kính tự nhiên của mắt, giúp điều chỉnh tiêu cự để tập trung ánh sáng lên võng mạc.
- Võng mạc: Lớp màng nhạy cảm với ánh sáng, nơi hình ảnh được tạo thành và chuyển hóa thành tín hiệu thần kinh gửi đến não.
2. Các Tật Khúc Xạ Của Mắt
- Cận thị: Khi mắt có trục quá dài hoặc giác mạc quá cong, làm cho hình ảnh tập trung trước võng mạc.
- Viễn thị: Xảy ra khi mắt có trục quá ngắn hoặc giác mạc quá phẳng, khiến hình ảnh tập trung sau võng mạc.
- Loạn thị: Do giác mạc không đều, dẫn đến hình ảnh không rõ nét tại bất kỳ khoảng cách nào.
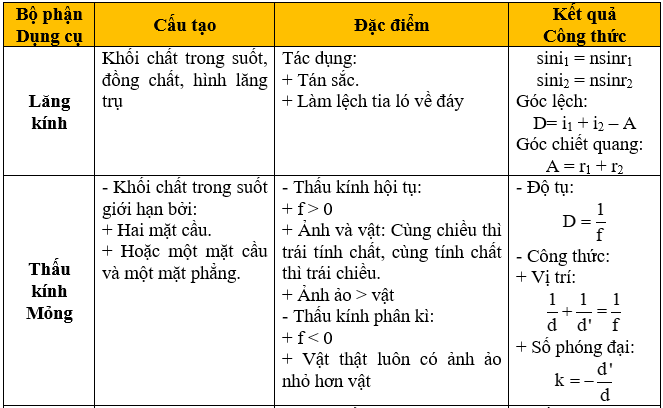
3. Các Dụng Cụ Quang Học Hỗ Trợ Mắt
Các dụng cụ quang học được thiết kế để khắc phục các tật khúc xạ của mắt hoặc giúp quan sát các vật thể nhỏ và xa:
- Kính lúp: Dùng để quan sát các chi tiết nhỏ bằng cách tạo ra hình ảnh phóng đại của vật thể.
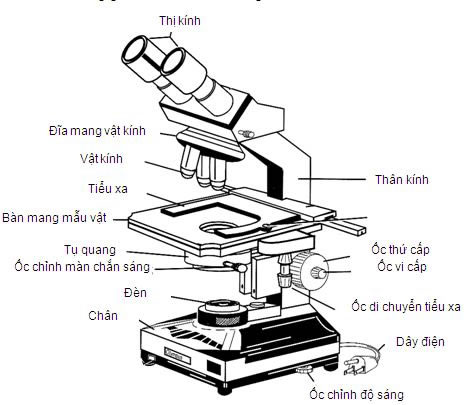
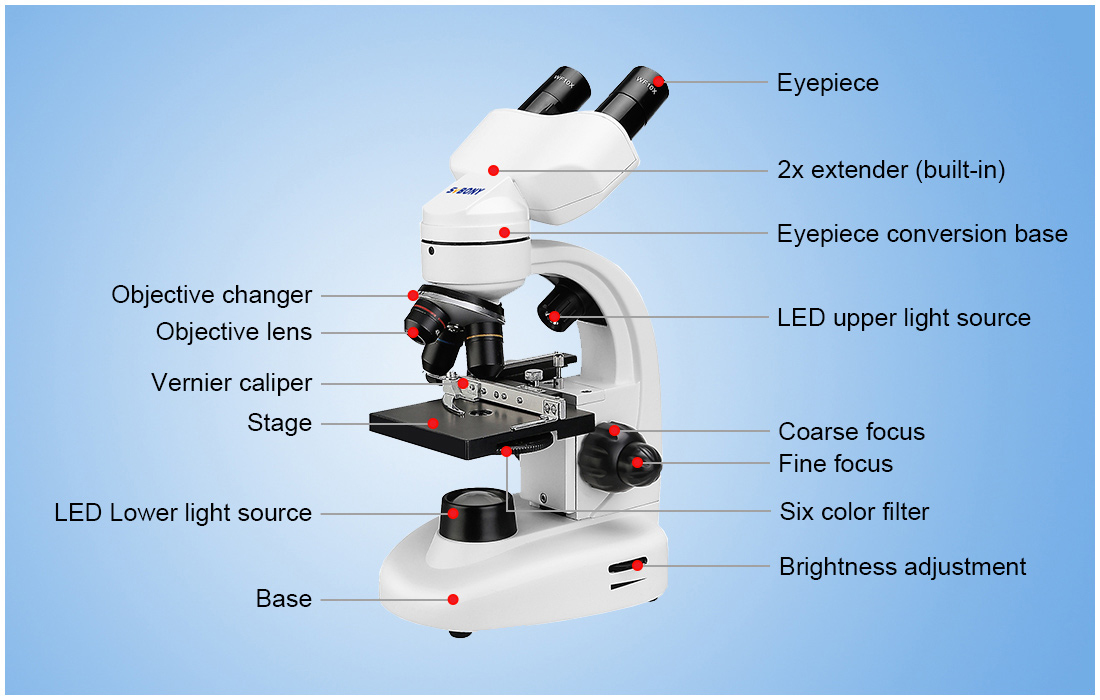
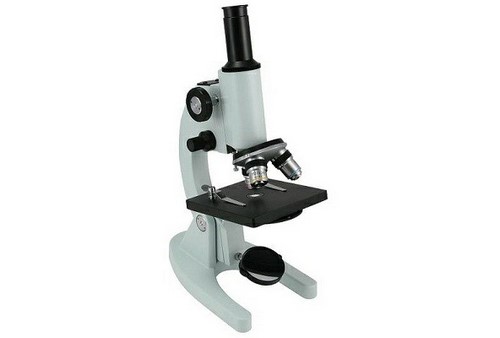
- Kính hiển vi: Sử dụng để quan sát các mẫu vật siêu nhỏ không thể thấy bằng mắt thường.
- Kính thiên văn: Dụng cụ quang học dùng để quan sát các vật thể ở rất xa như các ngôi sao và hành tinh.
- Kính mắt: Thường được sử dụng để điều chỉnh các tật khúc xạ của mắt, giúp người đeo nhìn rõ hơn.
4. Các Công Thức Quang Học Liên Quan
Các công thức quan trọng trong quang học liên quan đến mắt và dụng cụ quang học:
- Công thức thấu kính mỏng: \(\frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i}\), trong đó \(f\) là tiêu cự của thấu kính, \(d_o\) là khoảng cách từ vật đến thấu kính, và \(d_i\) là khoảng cách từ ảnh đến thấu kính.
- Số bội giác của kính lúp: \(G = 1 + \frac{D}{f}\), trong đó \(D\) là khoảng nhìn rõ của mắt và \(f\) là tiêu cự của kính lúp.
- Số bội giác của kính hiển vi: \(G = \frac{L}{f_1} \times \frac{D}{f_2}\), trong đó \(L\) là khoảng cách giữa hai thấu kính, \(f_1\) và \(f_2\) lần lượt là tiêu cự của thị kính và vật kính.
5. Vai Trò Của Dụng Cụ Quang Học Trong Cuộc Sống
Dụng cụ quang học không chỉ giúp điều chỉnh tật khúc xạ của mắt mà còn mở rộng khả năng quan sát của con người. Nhờ có kính hiển vi, chúng ta có thể khám phá thế giới vi mô; kính thiên văn giúp con người nhìn xa vào vũ trụ; còn kính lúp và kính mắt thì hỗ trợ trong các hoạt động hàng ngày và học tập.
| Dụng cụ | Ứng dụng |
|---|---|
| Kính lúp | Quan sát các vật thể nhỏ |
| Kính hiển vi | Nghiên cứu sinh học và y học |
| Kính thiên văn | Quan sát thiên văn học |
| Kính mắt | Điều chỉnh tật khúc xạ |
.png)
Mục Lục Tổng Hợp Về Mắt và Dụng Cụ Quang Học
Mục lục này sẽ cung cấp cái nhìn tổng quan và chi tiết về các chủ đề liên quan đến mắt và dụng cụ quang học, giúp bạn nắm bắt kiến thức một cách dễ dàng và khoa học.
-
1. Giới Thiệu Về Mắt
- 1.1. Cấu tạo của mắt và cách mắt hoạt động
- 1.2. Vai trò của các thành phần chính: Giác mạc, thủy tinh thể, võng mạc
- 1.3. Cơ chế tiếp nhận ánh sáng và truyền tín hiệu đến não
-
2. Các Tật Khúc Xạ Của Mắt
- 2.1. Cận thị: Nguyên nhân, triệu chứng và cách điều trị
- 2.2. Viễn thị: Đặc điểm và các phương pháp chỉnh sửa
- 2.3. Loạn thị: Hiểu rõ và các giải pháp hiệu quả
- 2.4. Lão thị: Thay đổi về tầm nhìn khi lão hóa
-
3. Dụng Cụ Quang Học Hỗ Trợ Thị Giác
- 3.1. Kính lúp: Cấu tạo, nguyên lý hoạt động và ứng dụng
- 3.2. Kính hiển vi: Loại kính, ứng dụng trong nghiên cứu
- 3.3. Kính thiên văn: Phân loại và cách sử dụng
- 3.4. Kính mắt: Các loại kính điều chỉnh tật khúc xạ
- 3.5. Kính áp tròng: Ưu và nhược điểm
-
4. Ứng Dụng Của Dụng Cụ Quang Học Trong Đời Sống
- 4.1. Vai trò của kính lúp trong công việc hàng ngày
- 4.2. Kính hiển vi và những tiến bộ trong y học
- 4.3. Kính thiên văn và khám phá vũ trụ
- 4.4. Sử dụng kính mắt trong đời sống hàng ngày
-
5. Công Thức Quang Học Liên Quan
- 5.1. Công thức thấu kính mỏng và ứng dụng trong tính toán
- 5.2. Số bội giác của kính lúp
- 5.3. Công thức tính số bội giác của kính hiển vi
- 5.4. Bài tập ứng dụng và giải pháp
-
6. Bài Tập Thực Hành
- 6.1. Bài tập về cấu tạo và chức năng của mắt
- 6.2. Bài tập về các tật khúc xạ và cách điều chỉnh
- 6.3. Bài tập về các dụng cụ quang học và ứng dụng của chúng
- 6.4. Bài tập tổng hợp về quang học trong đời sống
10 Dạng Bài Tập Toán Lý Về Mắt và Dụng Cụ Quang Học
Phần này tổng hợp 10 dạng bài tập toán lý liên quan đến mắt và dụng cụ quang học, nhằm giúp bạn củng cố kiến thức và áp dụng các công thức quang học vào thực tế. Mỗi bài tập đi kèm với hướng dẫn chi tiết để bạn dễ dàng nắm bắt và vận dụng.
-
Dạng 1: Tính tiêu cự của thấu kính mỏng
Cho một thấu kính hội tụ có độ tụ \(D = 5\) diop. Tính tiêu cự của thấu kính.
Lời giải: Sử dụng công thức tiêu cự của thấu kính: \[ f = \frac{1}{D} \].
-
Dạng 2: Xác định vị trí và tính chất của ảnh tạo bởi thấu kính
Một vật cao 5 cm đặt cách thấu kính hội tụ tiêu cự 10 cm một khoảng 15 cm. Xác định vị trí và tính chất của ảnh.
Lời giải: Áp dụng công thức thấu kính: \[ \frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i} \], sau đó tính chiều cao ảnh.
-
Dạng 3: Tính số bội giác của kính lúp
Một kính lúp có tiêu cự 10 cm. Tính số bội giác của kính lúp khi mắt đặt sát kính và nhìn ở vô cực.
Lời giải: Sử dụng công thức số bội giác: \[ G = 1 + \frac{D}{f} \].
-
Dạng 4: Giải bài toán về kính hiển vi
Kính hiển vi gồm vật kính có tiêu cự 1 cm và thị kính có tiêu cự 5 cm. Tính số bội giác khi khoảng cách giữa hai thấu kính là 20 cm.
Lời giải: Áp dụng công thức số bội giác của kính hiển vi: \[ G = \frac{L}{f_1} \times \frac{D}{f_2} \].
-
Dạng 5: Tính số bội giác của kính thiên văn
Kính thiên văn có vật kính tiêu cự 1 m và thị kính tiêu cự 5 cm. Tính số bội giác của kính thiên văn.
Lời giải: Sử dụng công thức: \[ G = \frac{f_1}{f_2} \].
-
Dạng 6: Xác định ảnh tạo bởi hệ thấu kính đồng trục
Một hệ gồm hai thấu kính hội tụ đồng trục có tiêu cự lần lượt là 10 cm và 20 cm, đặt cách nhau 30 cm. Tìm vị trí ảnh của một vật đặt trước thấu kính đầu tiên.
Lời giải: Giải từng bước bằng cách áp dụng công thức thấu kính cho từng thấu kính.
-
Dạng 7: Bài tập về tật cận thị và cách điều chỉnh
Một người bị cận thị có điểm cực viễn cách mắt 50 cm. Tính độ tụ của kính cận cần đeo để nhìn xa vô cực.
Lời giải: Sử dụng công thức độ tụ của kính cận: \[ D = \frac{1}{f} = \frac{1}{d_c} - \frac{1}{d_o} \].
-
Dạng 8: Tính toán liên quan đến kính viễn
Một người viễn thị có điểm cực cận cách mắt 100 cm. Tính độ tụ của kính viễn cần đeo để nhìn rõ vật cách mắt 25 cm.
Lời giải: Sử dụng công thức độ tụ kính viễn: \[ D = \frac{1}{d_c} - \frac{1}{d_o} \].
-
Dạng 9: Bài tập tổng hợp về quang học của mắt
Giải các bài toán liên quan đến việc xác định tiêu cự, tính số bội giác và điều chỉnh tật khúc xạ của mắt.
Lời giải: Áp dụng các công thức quang học để giải quyết các vấn đề.
-
Dạng 10: Bài tập về góc nhìn và độ phân giải của mắt
Tính góc nhìn tối thiểu và độ phân giải của mắt khi nhìn vật ở khoảng cách 25 cm.
Lời giải: Sử dụng công thức góc nhìn và các đặc tính quang học của mắt.

Bài Tập 1: Tính Toán Tiêu Cự Của Thấu Kính Mỏng
Bài tập này yêu cầu bạn tính tiêu cự của một thấu kính mỏng khi biết độ tụ của nó. Chúng ta sẽ đi qua từng bước chi tiết để giải quyết bài toán.
-
Đề Bài:
Một thấu kính hội tụ có độ tụ \(D = 2.5\) diop. Tính tiêu cự của thấu kính.
-
Bước 1: Xác định công thức liên quan
Tiêu cự \(f\) của thấu kính mỏng có mối quan hệ với độ tụ \(D\) thông qua công thức:
\[ f = \frac{1}{D} \]
-
Bước 2: Thay số vào công thức
Thay giá trị \(D = 2.5\) diop vào công thức:
\[ f = \frac{1}{2.5} \]
-
Bước 3: Tính toán kết quả
Thực hiện phép tính:
\[ f = 0.4 \, \text{m} = 40 \, \text{cm} \]
-
Kết Luận:
Tiêu cự của thấu kính mỏng này là 40 cm.

Bài Tập 2: Xác Định Số Bội Giác Của Kính Lúp
Kính lúp là một trong những dụng cụ quang học cơ bản, được sử dụng để phóng đại hình ảnh của vật thể nhỏ, giúp mắt người quan sát dễ dàng hơn. Trong bài tập này, chúng ta sẽ xác định số bội giác của kính lúp, một đại lượng quan trọng để đánh giá khả năng phóng đại của kính lúp.
Bước 1: Công thức xác định số bội giác của kính lúp
Số bội giác của kính lúp được tính bằng công thức:
\[ G = \dfrac{25}{f} \]
Trong đó:
- \( G \): Số bội giác của kính lúp
- \( f \): Tiêu cự của kính lúp (đơn vị cm)
Bước 2: Ví dụ minh họa
Giả sử ta có một kính lúp với tiêu cự \( f = 5 \, \text{cm} \). Hãy tính số bội giác \( G \) của kính lúp này.
Áp dụng công thức:
\[ G = \dfrac{25}{f} = \dfrac{25}{5} = 5 \]
Vậy số bội giác của kính lúp là 5, tức là kính lúp này có khả năng phóng đại hình ảnh lên gấp 5 lần so với khi nhìn bằng mắt thường.
Bước 3: Ứng dụng thực tế
Số bội giác của kính lúp càng lớn thì khả năng phóng đại càng cao, giúp người quan sát nhìn rõ các chi tiết nhỏ mà mắt thường không thể thấy. Kính lúp thường được sử dụng trong các lĩnh vực như y học, sinh học, và trong các ngành kỹ thuật cần kiểm tra các chi tiết nhỏ.
Bài tập bổ sung
Cho một kính lúp có tiêu cự \( f = 10 \, \text{cm} \). Hãy tính số bội giác của kính lúp này và nhận xét về khả năng phóng đại của nó so với ví dụ trên.

Bài Tập 3: Giải Bài Toán Về Kính Hiển Vi
Để giải một bài toán liên quan đến kính hiển vi, ta cần nắm vững các khái niệm và công thức cơ bản liên quan đến việc tạo ảnh trong kính hiển vi. Dưới đây là một quy trình giải bài toán cụ thể:
-
Xác định thông tin đề bài: Trước hết, cần xác định các yếu tố như tiêu cự của vật kính \(f_1\), tiêu cự của thị kính \(f_2\), và độ dài quang học của kính \(\delta\). Những yếu tố này thường được cung cấp trong đề bài.
-
Áp dụng công thức tạo ảnh: Kính hiển vi tạo ảnh qua hai bước:
-
Vật kính tạo ra một ảnh thật \({{A}_{1}'}{{B}_{1}'}\), lớn hơn vật nhiều lần và nằm trong khoảng \([O_2F_2]\).
-
Thị kính tạo ra một ảnh ảo sau cùng \({{A}_{2}'}{{B}_{2}'}\), là ảnh ảo lớn hơn vật nhiều lần và ngược chiều với vật.
-
-
Tính số bội giác: Số bội giác của kính hiển vi khi ngắm chừng ở vô cực được tính theo công thức:
\[
G_{\infty} = \left| k_1 \right| G_2 = \dfrac{\delta \cdot Đ}{f_1 \cdot f_2}
\]
Trong đó:
\[
\delta = Đ - f_1 - f_2
\]
Với \(Đ\) là khoảng cách từ vật đến vật kính, \(f_1\) là tiêu cự của vật kính và \(f_2\) là tiêu cự của thị kính. -
Áp dụng vào bài toán cụ thể: Dùng các giá trị cụ thể từ đề bài để thay vào công thức và tính toán số bội giác hoặc các yếu tố khác theo yêu cầu.
Khi giải bài toán về kính hiển vi, cần chú ý đến đơn vị đo và việc điều chỉnh khoảng cách sao cho ảnh cuối cùng hiện ra trong giới hạn nhìn rõ của mắt.
| Yếu tố | Ký hiệu | Giá trị |
| Tiêu cự vật kính | \(f_1\) | 1 cm |
| Tiêu cự thị kính | \(f_2\) | 4 cm |
| Độ dài quang học của kính | \(\delta\) | 20 cm |
| Khoảng cách từ vật đến vật kính | \(Đ\) | 22 cm |
XEM THÊM:
Bài Tập 4: Tính Số Bội Giác Của Kính Thiên Văn
Để giải bài toán về số bội giác của kính thiên văn, chúng ta cần hiểu rõ các khái niệm và công thức liên quan đến góc trông vật và góc trông ảnh qua kính.
1. Khái niệm:
- Góc trông vật (\(\alpha\)): Là góc tạo bởi hai tia sáng xuất phát từ hai điểm của vật đi qua quang tâm của vật kính.
- Góc trông ảnh (\(\beta\)): Là góc tạo bởi hai tia sáng xuất phát từ hai điểm của ảnh đi qua quang tâm của thị kính.
- Số bội giác (\(G\)): Được xác định bằng tỉ số giữa góc trông ảnh và góc trông vật, tức là: \[ G = \frac{\beta}{\alpha} \]
2. Công thức tính số bội giác của kính thiên văn:
Kính thiên văn bao gồm hai thấu kính: vật kính và thị kính. Khi đặt vật ở rất xa so với vật kính, ảnh của vật sẽ được tạo thành tại tiêu điểm của vật kính. Công thức tính số bội giác của kính thiên văn được cho bởi:
Trong đó:
- \(f_1\): tiêu cự của vật kính.
- \(f_2\): tiêu cự của thị kính.
3. Bài toán áp dụng:
Giả sử bạn có một kính thiên văn với tiêu cự của vật kính là \(f_1 = 1200 \, mm\) và tiêu cự của thị kính là \(f_2 = 50 \, mm\). Số bội giác của kính thiên văn này được tính như sau:
Vậy số bội giác của kính thiên văn là 24 lần. Điều này có nghĩa là ảnh của vật quan sát qua kính thiên văn sẽ lớn hơn vật quan sát bằng mắt thường 24 lần.
Qua bài toán này, chúng ta thấy rõ vai trò quan trọng của tiêu cự của các thấu kính trong việc xác định độ phóng đại của kính thiên văn. Việc lựa chọn các thấu kính phù hợp sẽ giúp cải thiện khả năng quan sát các vật thể ở xa.

Bài Tập 5: Ứng Dụng Công Thức Thấu Kính Mỏng Trong Các Bài Toán
Trong bài tập này, chúng ta sẽ áp dụng công thức thấu kính mỏng để giải quyết các bài toán liên quan đến sự hội tụ hoặc phân kỳ của ánh sáng qua các loại thấu kính khác nhau. Công thức chính sử dụng trong bài toán là:
Trong đó:
- \(f\) là tiêu cự của thấu kính.
- \(d_o\) là khoảng cách từ vật đến thấu kính.
- \(d_i\) là khoảng cách từ ảnh đến thấu kính.
Để giải một bài toán cụ thể, chúng ta có thể thực hiện theo các bước sau:
- Bước 1: Xác định các đại lượng đã biết trong bài toán, như khoảng cách từ vật đến thấu kính (\(d_o\)), và đặc điểm của ảnh (thật hay ảo, cùng chiều hay ngược chiều).
- Bước 2: Sử dụng công thức thấu kính mỏng để tìm tiêu cự của thấu kính.
- Bước 3: Xác định tính chất của ảnh qua các dấu hiệu của tiêu cự và khoảng cách từ ảnh đến thấu kính.
- Bước 4: Kiểm tra lại kết quả và suy luận ra các đặc điểm bổ sung nếu cần thiết.
Ví dụ minh họa:
Giả sử ta có một thấu kính hội tụ với tiêu cự \(f = 10 \, cm\). Một vật được đặt cách thấu kính \(d_o = 15 \, cm\). Hãy tính khoảng cách từ ảnh đến thấu kính.
Áp dụng công thức:
Giải phương trình trên để tìm \(d_i\):
Vậy ảnh của vật sẽ được tạo thành tại vị trí cách thấu kính 30 cm, cùng phía với vật.

Bài Tập 6: Phân Tích Hình Ảnh Tạo Bởi Kính Lúp
Kính lúp là một dụng cụ quang học quan trọng, thường được sử dụng để phóng đại hình ảnh của các vật nhỏ. Khi một vật được đặt trong khoảng tiêu cự của kính lúp, hình ảnh sẽ được tạo ra và phân tích theo các bước sau:
- Đặt vật trong khoảng tiêu cự của kính lúp: Vật cần quan sát được đặt ở khoảng cách nhỏ hơn tiêu cự của kính lúp (khoảng cách từ kính đến vật ký hiệu là \(d\)).
- Xác định tiêu cự \(f\) của kính lúp: Tiêu cự là khoảng cách từ thấu kính đến điểm mà các tia sáng hội tụ lại (điểm ảnh thật). Ví dụ, kính lúp có tiêu cự \(f = 10cm\).
- Phân tích hình ảnh: Hình ảnh được tạo bởi kính lúp là một ảnh ảo, lớn hơn và cùng chiều với vật.
- Công thức cơ bản: Sử dụng công thức thấu kính mỏng \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{d'}\), trong đó \(d'\) là khoảng cách từ ảnh đến kính, để xác định vị trí ảnh.
- Phóng đại của kính lúp: Độ phóng đại \(M\) được xác định bởi công thức \[M = \dfrac{25cm}{f}\] với 25cm là khoảng cách ngắn nhất mà mắt có thể nhìn rõ.
- Quan sát hình ảnh: Hình ảnh quan sát qua kính lúp sẽ rõ nét và lớn hơn nhiều so với khi quan sát bằng mắt thường, tạo điều kiện thuận lợi cho việc nghiên cứu các chi tiết nhỏ.
Qua việc phân tích này, ta có thể thấy rằng kính lúp là một công cụ hữu ích trong nhiều lĩnh vực như nghiên cứu khoa học, y học, và cả trong đời sống hàng ngày.
Bài Tập 7: Giải Các Bài Toán Liên Quan Đến Tật Khúc Xạ Của Mắt
Trong chương trình Vật lý lớp 11, các bài toán liên quan đến tật khúc xạ của mắt là một phần quan trọng giúp học sinh nắm vững kiến thức về cách mà các dụng cụ quang học như kính lúp, kính hiển vi, và kính thiên văn hỗ trợ trong việc cải thiện thị lực.
Bài tập này sẽ giúp bạn giải quyết các vấn đề liên quan đến tật khúc xạ của mắt, đặc biệt là cận thị, viễn thị và lão thị. Hãy cùng đi qua từng bước để hiểu rõ hơn về cách tính toán và áp dụng các công thức vào giải bài toán.
- Bước 1: Xác định loại tật khúc xạ
Đầu tiên, bạn cần xác định được loại tật khúc xạ mà mắt gặp phải. Mắt bị cận thị sẽ không nhìn rõ được các vật ở xa, trong khi mắt bị viễn thị khó nhìn rõ các vật ở gần. Mắt lão thị thường gặp ở người già, làm giảm khả năng điều tiết khi nhìn các vật ở khoảng cách khác nhau.
- Bước 2: Áp dụng công thức tính tiêu cự
Với các loại kính dùng để điều chỉnh tật khúc xạ, bạn cần áp dụng công thức tính tiêu cự của kính:
\[ \frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i} \]
Trong đó:
- \(f\): Tiêu cự của kính
- \(d_o\): Khoảng cách từ vật đến kính
- \(d_i\): Khoảng cách từ ảnh đến kính (có thể là khoảng cách từ kính đến võng mạc mắt)
- Bước 3: Giải quyết các bài toán cụ thể
Ví dụ, với một bài toán về mắt cận thị, hãy tính tiêu cự của kính cần đeo để mắt có thể nhìn rõ vật ở vô cực:
\[ \frac{1}{f} = \frac{1}{d_{\text{voo cuc}}} + \frac{1}{d_i} \]
Giả sử mắt cận có tiêu cự tự nhiên là -60cm (tiêu cự âm chỉ mắt cận), bạn có thể thay vào công thức để tìm tiêu cự của kính cần đeo.
- Bước 4: Đánh giá và kết luận
Sau khi giải xong bài toán, bạn nên đánh giá lại kết quả xem có hợp lý với thực tế không, đồng thời ghi nhớ công thức và phương pháp để áp dụng cho các bài toán khác.
Bài tập này không chỉ giúp bạn hiểu rõ hơn về các tật khúc xạ mà còn cung cấp kiến thức để áp dụng vào thực tế, như chọn kính phù hợp để điều chỉnh tật khúc xạ.

Bài Tập 8: Giải Bài Toán Về Hệ Thấu Kính Đồng Trục
Trong bài tập này, chúng ta sẽ cùng tìm hiểu cách giải các bài toán liên quan đến hệ thấu kính đồng trục. Hệ thấu kính đồng trục bao gồm hai hoặc nhiều thấu kính được sắp xếp sao cho các trục chính của chúng trùng nhau. Bài toán thường yêu cầu tính khoảng cách ảnh, độ phóng đại, và các thông số khác của hệ thấu kính.
Bước 1: Xác định các thông số cơ bản của thấu kính.
- Tiêu cự \( f_1 \) của thấu kính thứ nhất
- Tiêu cự \( f_2 \) của thấu kính thứ hai
- Khoảng cách giữa hai thấu kính \( d \)
Bước 2: Sử dụng công thức tính tiêu cự của hệ thấu kính đồng trục.
Công thức tổng quát để tính tiêu cự hiệu dụng của hệ thấu kính đồng trục là:
Trong đó:
- \( f_{\text{hệ}} \): Tiêu cự của hệ thấu kính
- \( f_1 \): Tiêu cự của thấu kính thứ nhất
- \( f_2 \): Tiêu cự của thấu kính thứ hai
- \( d \): Khoảng cách giữa hai thấu kính
Bước 3: Xác định vị trí và tính chất của ảnh.
Sau khi tính được tiêu cự của hệ thấu kính, ta có thể sử dụng công thức thấu kính mỏng để xác định vị trí ảnh:
Trong đó:
- \( d_{\text{vật}} \): Khoảng cách từ vật đến thấu kính đầu tiên
- \( d_{\text{ảnh}} \): Khoảng cách từ ảnh đến thấu kính cuối cùng
Bước 4: Tính độ phóng đại của hệ thấu kính.
Độ phóng đại của hệ thấu kính được xác định bằng tích của độ phóng đại của từng thấu kính:
Trong đó:
- \( M_1 = \frac{d_{\text{ảnh}1}}{d_{\text{vật}}} \): Độ phóng đại của thấu kính thứ nhất
- \( M_2 = \frac{d_{\text{ảnh}2}}{d_{\text{ảnh}1}} \): Độ phóng đại của thấu kính thứ hai
Bước 5: Tổng hợp và kiểm tra kết quả.
Sau khi đã tính toán đầy đủ các thông số, cần kiểm tra lại các giá trị và xác định xem kết quả có hợp lý hay không. Nếu cần, hãy sử dụng hình vẽ để minh họa vị trí vật và ảnh, cũng như các tia sáng chính qua hệ thấu kính.
Như vậy, với các bước trên, chúng ta có thể giải quyết các bài toán liên quan đến hệ thấu kính đồng trục một cách chi tiết và hiệu quả.
Bài Tập 9: Tính Toán Liên Quan Đến Kính Viễn Và Kính Cận
Trong bài tập này, chúng ta sẽ tìm hiểu cách tính toán liên quan đến kính viễn và kính cận, những loại kính dùng để điều chỉnh tật khúc xạ của mắt. Cụ thể, chúng ta sẽ sử dụng công thức và lý thuyết quang học để giải các bài toán.
Bước 1: Xác định công thức liên quan
- Với kính cận: Công thức sử dụng là công thức thấu kính mỏng \(\frac{1}{f} = \frac{1}{d} + \frac{1}{d'}\), trong đó \(f\) là tiêu cự của kính, \(d\) là khoảng cách từ vật đến kính, và \(d'\) là khoảng cách từ ảnh đến kính.
- Với kính viễn: Công thức tương tự như kính cận, nhưng chú ý đến khoảng cách vô cùng lớn của vật khi xem qua kính.
Bước 2: Áp dụng công thức vào bài toán cụ thể
- Xác định các giá trị ban đầu như tiêu cự \(f\), khoảng cách từ vật đến kính \(d\), và khoảng cách từ ảnh đến kính \(d'\).
- Thay các giá trị này vào công thức \(\frac{1}{f} = \frac{1}{d} + \frac{1}{d'}\) để tính toán tiêu cự của kính hoặc các yếu tố còn thiếu khác.
- Kiểm tra kết quả bằng cách tính ngược lại và đảm bảo rằng kết quả phù hợp với điều kiện bài toán.
Bước 3: Phân tích kết quả và thực hiện kiểm tra
- Đối với kính cận: Xác định xem tiêu cự của kính có nằm trong phạm vi hợp lý cho người dùng cận thị hay không.
- Đối với kính viễn: Đảm bảo rằng các tính toán đúng với thực tế, đặc biệt khi áp dụng vào các bài toán với khoảng cách xa.
Cuối cùng, hãy tổng hợp lại các bước tính toán và đưa ra kết luận cho bài toán. Điều quan trọng là phải hiểu rõ cơ sở lý thuyết để áp dụng đúng công thức và đưa ra kết quả chính xác.
Bài Tập 10: Bài Tập Tổng Hợp Về Quang Học Liên Quan Đến Mắt
Trong bài tập này, chúng ta sẽ áp dụng các kiến thức về quang học liên quan đến mắt để giải quyết các bài toán tổng hợp. Mắt người hoạt động như một hệ quang học phức tạp với các thành phần như thấu kính và màng lưới. Dưới đây là các bài tập giúp củng cố kiến thức:
-
Bài tập 1: Tính khoảng cách từ vật đến mắt khi mắt quan sát rõ vật.
Giả sử một người có mắt bình thường, nghĩa là khoảng cách từ mắt đến vật xa nhất mà người đó vẫn nhìn rõ là vô cực. Hãy tính khoảng cách từ vật đến mắt khi người này quan sát rõ vật ở khoảng cách 25 cm.
Hướng dẫn:
- Sử dụng công thức thấu kính hội tụ: \[ \frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i} \]
- Trong đó, \( f \) là tiêu cự của thấu kính, \( d_o \) là khoảng cách từ vật đến mắt, và \( d_i \) là khoảng cách từ thấu kính đến ảnh (khoảng cách từ mắt đến điểm cực cận).
- Áp dụng giá trị \( d_i = -25 \, cm \) và \( d_o = \infty \) để tìm tiêu cự \( f \).
-
Bài tập 2: Tính độ phóng đại của ảnh qua kính hiển vi.
Khi sử dụng kính hiển vi để quan sát một vật nhỏ, độ phóng đại của ảnh được tính bằng tích của độ phóng đại của kính hiển vi và kính mắt.
Hướng dẫn:
- Sử dụng công thức: \[ M = M_{\text{kính hiển vi}} \times M_{\text{kính mắt}} \]
- Trong đó, \( M_{\text{kính hiển vi}} \) là độ phóng đại của kính hiển vi, và \( M_{\text{kính mắt}} \) là độ phóng đại của kính mắt.
- Xác định giá trị từng thành phần và tính \( M \).
-
Bài tập 3: Tính toán liên quan đến kính viễn.
Một người bị tật viễn thị có điểm cực cận ở khoảng cách 50 cm. Hãy xác định độ tụ của kính viễn để người đó có thể đọc sách ở khoảng cách 25 cm.
Hướng dẫn:
- Dùng công thức tính độ tụ: \[ D = \frac{1}{f} \]
- Với \( D \) là độ tụ của kính, \( f \) là tiêu cự tính bằng mét. Sử dụng công thức: \[ D = \frac{1}{d_{\text{cận}}} - \frac{1}{d_{\text{viễn}}} \]
- Với \( d_{\text{cận}} \) là khoảng cách từ mắt đến điểm cực cận mới (25 cm) và \( d_{\text{viễn}} \) là khoảng cách từ mắt đến điểm cực cận cũ (50 cm).