Các Dụng Cụ Quang Học Bổ Trợ Cho Mắt: Tìm Hiểu Toàn Diện Và Ứng Dụng Thực Tế

Các dụng cụ quang học bổ trợ cho mắt là những thiết bị quan trọng trong việc hỗ trợ và cải thiện khả năng nhìn của con người. Dưới đây là tổng hợp chi tiết về các dụng cụ này.

1. Kính Lúp

Kính lúp là một dụng cụ quang học giúp phóng đại hình ảnh của các vật thể nhỏ. Khi sử dụng kính lúp, hình ảnh của vật thể sẽ được phóng to, giúp người dùng quan sát chi tiết hơn.

1. Cấu tạo: Gồm một thấu kính hội tụ có tiêu cự ngắn.
2. Nguyên lý hoạt động: Kính lúp tạo ra một ảnh ảo lớn hơn vật thật khi vật được đặt trong khoảng tiêu cự.
3. Công dụng: Dùng để quan sát các vật nhỏ như tem, côn trùng, hoặc các chi tiết nhỏ trên bản vẽ.

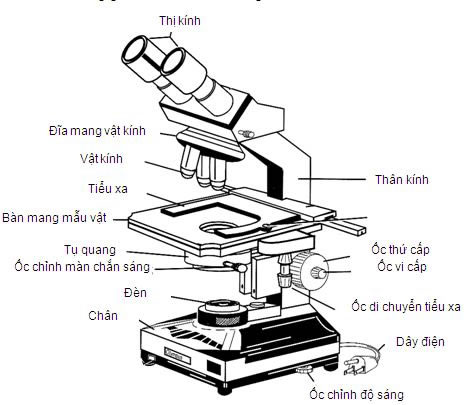
2. Kính Hiển Vi

Kính hiển vi là dụng cụ quan trọng trong nghiên cứu khoa học, đặc biệt là trong các lĩnh vực như sinh học và y học. Nó giúp phóng đại hình ảnh của các mẫu vật nhỏ đến mức có thể quan sát được tế bào.

1. Cấu tạo: Gồm một hoặc nhiều thấu kính hội tụ và có hệ thống điều chỉnh ánh sáng.
2. Nguyên lý hoạt động: Kính hiển vi sử dụng nhiều thấu kính để phóng đại hình ảnh mẫu vật và truyền ảnh đến mắt người quan sát.
3. Công dụng: Dùng trong nghiên cứu tế bào, vi khuẩn, và các vi sinh vật khác.

3. Kính Thiên Văn

Kính thiên văn là một dụng cụ quang học được sử dụng để quan sát các vật thể ở xa như các hành tinh, ngôi sao và các thiên thể khác trong vũ trụ.

1. Cấu tạo: Gồm một thấu kính lớn hoặc một hệ thống gương phản chiếu.
2. Nguyên lý hoạt động: Kính thiên văn thu thập ánh sáng từ các vật thể ở xa và hội tụ chúng lại thành một hình ảnh rõ ràng.
3. Công dụng: Dùng để quan sát và nghiên cứu các thiên thể, giúp chúng ta hiểu biết thêm về vũ trụ.

4. Kính Cận và Kính Viễn

Kính cận và kính viễn là hai loại kính phổ biến nhất được sử dụng để điều chỉnh các tật khúc xạ của mắt.

1. Kính cận: Sử dụng thấu kính phân kỳ để giúp người bị cận thị nhìn rõ hơn các vật ở xa.
2. Kính viễn: Sử dụng thấu kính hội tụ để giúp người bị viễn thị nhìn rõ hơn các vật ở gần.

5. Kính Áp Tròng

Kính áp tròng là một loại kính nhỏ, mỏng, đặt trực tiếp lên bề mặt giác mạc của mắt. Chúng được thiết kế để điều chỉnh tật khúc xạ mà không cần đeo kính gọng.

1. Loại kính: Có hai loại chính là kính áp tròng mềm và kính áp tròng cứng.
2. Nguyên lý hoạt động: Kính áp tròng giúp điều chỉnh ánh sáng đi qua giác mạc và thủy tinh thể để hình ảnh được hội tụ đúng trên võng mạc.
3. Công dụng: Thường được sử dụng cho người có nhu cầu thẩm mỹ hoặc hoạt động thể thao.

Kết Luận

Các dụng cụ quang học bổ trợ cho mắt đóng vai trò quan trọng trong việc cải thiện và hỗ trợ thị lực của con người. Từ kính lúp đến kính thiên văn, mỗi dụng cụ đều có cấu tạo và chức năng đặc biệt, đáp ứng nhu cầu đa dạng của người sử dụng.

Các dụng cụ quang học bổ trợ cho mắt là những thiết bị quan trọng trong việc hỗ trợ và cải thiện khả năng nhìn của con người. Dưới đây là mục lục tổng hợp các dụng cụ này, được phân loại chi tiết để người đọc có cái nhìn toàn diện và rõ ràng.

• Kính Lúp:

  Kính lúp là một dụng cụ quang học giúp phóng đại hình ảnh của các vật thể nhỏ. Kính lúp được sử dụng phổ biến trong các hoạt động như đọc sách, quan sát tem thư, và nghiên cứu chi tiết nhỏ.

• Kính Hiển Vi:

  Kính hiển vi giúp phóng đại hình ảnh của các mẫu vật nhỏ đến mức có thể quan sát được tế bào. Đây là một dụng cụ không thể thiếu trong các phòng thí nghiệm sinh học và y học.

• Kính Thiên Văn:

  Kính thiên văn được sử dụng để quan sát các thiên thể như sao, hành tinh và các vật thể xa xôi trong vũ trụ. Loại kính này đặc biệt hữu ích cho các nhà thiên văn học và những người yêu thích khám phá bầu trời đêm.

• Kính Cận và Kính Viễn:

  Kính cận và kính viễn là hai loại kính phổ biến nhất được sử dụng để điều chỉnh các tật khúc xạ của mắt, giúp cải thiện thị lực cho người bị cận thị hoặc viễn thị.

• Kính Áp Tròng:

  Kính áp tròng là một lựa chọn thẩm mỹ và tiện lợi cho những người không muốn đeo kính gọng. Kính áp tròng có nhiều loại khác nhau, phục vụ cho cả mục đích thẩm mỹ và điều chỉnh thị lực.

• Ống Nhòm:

  Ống nhòm là dụng cụ giúp phóng to hình ảnh của các vật thể ở xa. Nó thường được sử dụng trong các hoạt động ngoài trời như săn bắn, quan sát chim chóc, và thể thao.

• Kính Râm:

  Kính râm không chỉ giúp bảo vệ mắt khỏi ánh sáng mặt trời mà còn là một phụ kiện thời trang. Kính râm có nhiều loại, từ kính phân cực đến kính thời trang với nhiều màu sắc và kiểu dáng.

• Kính Bảo Hộ:

  Kính bảo hộ được sử dụng để bảo vệ mắt trong các môi trường nguy hiểm như xây dựng, làm việc với hóa chất, hoặc trong các phòng thí nghiệm. Đây là một dụng cụ không thể thiếu để đảm bảo an toàn lao động.

Việc hiểu rõ về các dụng cụ quang học bổ trợ cho mắt sẽ giúp bạn chọn lựa và sử dụng chúng một cách hiệu quả, đồng thời bảo vệ và cải thiện sức khỏe thị giác của mình.

Trong vật lý, số bội giác của kính lúp là chỉ số quan trọng để đánh giá khả năng phóng đại của kính. Để giải bài tập này, chúng ta cần thực hiện các bước sau:

1. Định nghĩa số bội giác:

   Số bội giác (\(M\)) là tỉ số giữa kích thước của ảnh thu được qua kính lúp và kích thước của vật khi nhìn trực tiếp bằng mắt thường ở khoảng cách rõ nhất.

2. Công thức tính số bội giác:

   Số bội giác của kính lúp được tính bằng công thức:
   \[
   M = \frac{25}{f}
   \]
   trong đó \(25\) là khoảng cách nhìn rõ nhất của mắt người tính bằng cm, và \(f\) là tiêu cự của kính lúp cũng tính bằng cm.

3. Áp dụng công thức:

   Giả sử bạn có một kính lúp có tiêu cự \(f = 5 \, cm\), số bội giác của kính lúp sẽ là:
   \[
   M = \frac{25}{5} = 5
   \]
   Vậy, số bội giác của kính lúp là 5, nghĩa là kích thước của ảnh qua kính lúp lớn gấp 5 lần so với kích thước của vật nhìn trực tiếp.

4. Kiểm tra kết quả:

   Đảm bảo rằng các đơn vị đo lường là chính xác và kết quả tính toán hợp lý so với thực tế sử dụng kính lúp.

Bằng cách áp dụng công thức đơn giản trên, bạn có thể dễ dàng tính toán và xác định số bội giác của bất kỳ kính lúp nào, giúp bạn hiểu rõ hơn về hiệu quả của dụng cụ quang học này.

Tiêu cự của thấu kính trong kính hiển vi là một yếu tố quan trọng để xác định khả năng phóng đại của kính. Dưới đây là các bước để tính toán tiêu cự của thấu kính:

1. Định nghĩa tiêu cự:

   Tiêu cự (\(f\)) của một thấu kính là khoảng cách từ thấu kính đến tiêu điểm, nơi mà các tia sáng hội tụ hoặc phân kỳ sau khi đi qua thấu kính.

2. Công thức liên quan:

   Tiêu cự của thấu kính trong kính hiển vi được tính bằng công thức:
   \[
   \frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i}
   \]
   trong đó \(d_o\) là khoảng cách từ vật đến thấu kính và \(d_i\) là khoảng cách từ thấu kính đến ảnh.

3. Áp dụng công thức:

   Giả sử bạn có một kính hiển vi với \(d_o = 2 \, cm\) và \(d_i = 10 \, cm\). Tiêu cự của thấu kính sẽ là:
   \[
   \frac{1}{f} = \frac{1}{2} + \frac{1}{10} = \frac{5}{10} + \frac{1}{10} = \frac{6}{10} = \frac{3}{5}
   \]
   Do đó, tiêu cự \(f\) sẽ là:
   \[
   f = \frac{5}{3} \approx 1.67 \, cm
   \]
   Vậy, tiêu cự của thấu kính trong trường hợp này là khoảng \(1.67 \, cm\).

4. Kiểm tra kết quả:

   Đảm bảo rằng kết quả tiêu cự hợp lý dựa trên các thông số của kính hiển vi. Kiểm tra đơn vị đo lường và xác nhận tính toán đã chính xác.

Thông qua việc áp dụng công thức trên, bạn có thể dễ dàng tính toán tiêu cự của thấu kính trong kính hiển vi, giúp tối ưu hóa khả năng quan sát và phân tích mẫu vật.

Khi sử dụng kính thiên văn, việc xác định khoảng cách từ kính đến vật thể là một yếu tố quan trọng để có thể quan sát rõ ràng và chính xác. Dưới đây là các bước chi tiết để xác định khoảng cách vật thể khi sử dụng kính thiên văn:

1. Xác định tiêu cự của kính thiên văn:

   Tiêu cự của kính thiên văn (\(f\)) là khoảng cách từ thấu kính chính đến tiêu điểm nơi mà các tia sáng hội tụ. Thông thường, thông số này được nhà sản xuất cung cấp hoặc có thể được tính toán dựa trên cấu tạo của kính.

2. Sử dụng công thức khoảng cách:

   Công thức liên hệ giữa tiêu cự (\(f\)), khoảng cách từ vật thể đến kính thiên văn (\(d_o\)), và khoảng cách từ ảnh đến kính thiên văn (\(d_i\)) là:
   \[
   \frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i}
   \]
   Trong đó, \(d_o\) là khoảng cách từ vật thể đến kính, và \(d_i\) là khoảng cách từ kính đến ảnh của vật thể.

3. Tính toán khoảng cách vật thể:

   Giả sử bạn có một kính thiên văn với tiêu cự \(f = 20 \, cm\), và khoảng cách từ ảnh đến kính thiên văn \(d_i = 100 \, cm\). Ta có thể xác định khoảng cách vật thể \(d_o\) bằng cách:
   \[
   \frac{1}{d_o} = \frac{1}{f} - \frac{1}{d_i} = \frac{1}{20} - \frac{1}{100} = \frac{5}{100} - \frac{1}{100} = \frac{4}{100} = \frac{1}{25}
   \]
   Do đó, khoảng cách từ vật thể đến kính thiên văn \(d_o = 25 \, cm\).

4. Kiểm tra và hiệu chỉnh:

   Sau khi tính toán, kiểm tra lại các đơn vị và kết quả để đảm bảo khoảng cách vật thể là hợp lý và phù hợp với việc quan sát bằng kính thiên văn.

Với việc áp dụng đúng công thức và thực hiện các bước tính toán chi tiết, bạn có thể xác định chính xác khoảng cách từ vật thể đến kính thiên văn, giúp tối ưu hóa việc quan sát các thiên thể trong không gian.

Kính cận là loại kính sử dụng thấu kính phân kỳ để điều chỉnh tật khúc xạ cận thị, giúp người sử dụng nhìn rõ vật thể ở xa. Việc phân tích ảnh qua kính cận là một bài toán phổ biến trong quang học. Dưới đây là các bước phân tích chi tiết:

1. Xác định đặc điểm của kính cận:

   Kính cận sử dụng thấu kính phân kỳ, có tiêu cự âm (\(f < 0\)). Ảnh của vật thể qua kính cận luôn là ảnh ảo, nằm cùng phía với vật thể so với kính.

2. Công thức liên quan:

   Công thức tính vị trí và độ lớn của ảnh qua kính cận:
   \[
   \frac{1}{f} = \frac{1}{d_o} - \frac{1}{d_i}
   \]
   Trong đó:
   

   
   
   • \(f\): tiêu cự của thấu kính.
   
   
   • \(d_o\): khoảng cách từ vật thể đến kính.
   
   
   • \(d_i\): khoảng cách từ ảnh đến kính.
   
   
   
   


3. Phân tích ảnh:

   Giả sử bạn có một kính cận với tiêu cự \(f = -50 \, cm\), và vật thể cách kính \(d_o = 25 \, cm\). Ta có thể tính khoảng cách ảnh \(d_i\) bằng cách:
   \[
   \frac{1}{-50} = \frac{1}{25} - \frac{1}{d_i} \Rightarrow \frac{1}{d_i} = \frac{1}{25} + \frac{1}{50} = \frac{2 + 1}{50} = \frac{3}{50}
   \]
   Do đó, khoảng cách ảnh \(d_i = \frac{50}{3} \approx 16.67 \, cm\) (ảnh ảo, nằm cùng phía với vật thể).

4. Kiểm tra và vẽ hình minh họa:

   Sau khi tính toán, bạn có thể vẽ hình minh họa để kiểm tra tính chính xác của việc phân tích ảnh qua kính cận. Điều này giúp hình dung rõ hơn về cách ảnh ảo được tạo ra và cách nó ảnh hưởng đến thị giác của người sử dụng.

Thông qua quá trình phân tích trên, bạn có thể hiểu rõ hơn về cách kính cận hoạt động và cách nó giúp cải thiện tầm nhìn cho người bị cận thị.

Kính viễn là dụng cụ quang học giúp quan sát các vật thể ở xa với độ phóng đại cao. Để tính toán độ phóng đại của kính viễn, chúng ta cần hiểu các yếu tố ảnh hưởng và công thức cơ bản. Dưới đây là hướng dẫn chi tiết từng bước:

1. Xác định tiêu cự của kính viễn:

   Kính viễn thường bao gồm hai thấu kính: thấu kính vật kính và thấu kính thị kính. Tiêu cự của thấu kính vật kính (\(f_o\)) và thấu kính thị kính (\(f_e\)) là các thông số chính để tính độ phóng đại.

2. Công thức tính độ phóng đại:

   Độ phóng đại của kính viễn được tính bằng công thức:
   \[
   M = \frac{f_o}{f_e}
   \]
   Trong đó:
   

   
   
   • \(M\): độ phóng đại của kính viễn.
   
   
   • \(f_o\): tiêu cự của thấu kính vật kính.
   
   
   • \(f_e\): tiêu cự của thấu kính thị kính.
   
   
   
   


3. Ví dụ cụ thể:

   Giả sử bạn có một kính viễn với tiêu cự của thấu kính vật kính là \(f_o = 500 \, mm\) và tiêu cự của thấu kính thị kính là \(f_e = 25 \, mm\). Độ phóng đại của kính viễn được tính như sau:
   \[
   M = \frac{500 \, mm}{25 \, mm} = 20
   \]
   Như vậy, độ phóng đại của kính viễn là 20 lần.

4. Thực hành và kiểm tra kết quả:

   Sau khi tính toán, bạn có thể sử dụng kính viễn để quan sát và kiểm tra thực tế độ phóng đại. Điều này giúp đảm bảo rằng các giá trị lý thuyết phù hợp với thực tiễn.

Việc nắm vững cách tính độ phóng đại của kính viễn không chỉ giúp bạn hiểu rõ hơn về cấu tạo và chức năng của kính viễn mà còn cải thiện kỹ năng sử dụng các dụng cụ quang học trong các tình huống thực tế.

Kính áp tròng là một loại dụng cụ quang học được thiết kế để đặt trực tiếp lên bề mặt của mắt, giúp điều chỉnh tật khúc xạ và cải thiện thị lực. Việc phân tích ảnh qua kính áp tròng có thể giúp chúng ta hiểu rõ hơn về cách thức hoạt động của loại kính này và tối ưu hóa việc sử dụng trong các trường hợp cụ thể.

Để phân tích ảnh qua kính áp tròng, chúng ta cần xem xét các yếu tố sau:

1. Chiết suất của kính áp tròng: Kính áp tròng có chiết suất khác nhau tùy vào vật liệu chế tạo. Thông thường, chiết suất của kính áp tròng cao hơn chiết suất của không khí, giúp hội tụ ánh sáng vào võng mạc. Chúng ta có thể sử dụng công thức tính chiết suất: \[ n = \frac{c}{v} \] Trong đó:
   • \(n\): Chiết suất của vật liệu
   • \(c\): Vận tốc ánh sáng trong chân không
   • \(v\): Vận tốc ánh sáng trong vật liệu
2. Độ cong của kính áp tròng: Độ cong của kính ảnh hưởng trực tiếp đến cách ánh sáng được hội tụ. Kính có độ cong càng lớn thì khả năng hội tụ càng cao, giúp điều chỉnh các vấn đề như cận thị hoặc viễn thị. Công thức tính tiêu cự \(f\) của thấu kính là: \[ \frac{1}{f} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) \] Trong đó:
   • \(R_1\): Bán kính cong của mặt trước kính áp tròng
   • \(R_2\): Bán kính cong của mặt sau kính áp tròng
3. Độ dày của kính áp tròng: Độ dày không chỉ ảnh hưởng đến độ thoải mái khi đeo mà còn ảnh hưởng đến cách thức ánh sáng đi qua kính. Độ dày trung bình của kính áp tròng thường là một vài millimet và phải được tính toán kỹ lưỡng để đảm bảo hình ảnh rõ nét và không bị méo mó.

Qua việc hiểu rõ các thông số kỹ thuật này, chúng ta có thể phân tích và điều chỉnh kính áp tròng phù hợp với từng người dùng cụ thể, giúp cải thiện chất lượng thị giác và nâng cao hiệu quả sử dụng kính áp tròng trong đời sống hàng ngày.

Trong dạng bài tập này, chúng ta sẽ tìm hiểu cách tính chiết suất của thấu kính trong kính hiển vi bằng cách sử dụng công thức vật lý cơ bản và một số bước tính toán cụ thể. Để làm điều này, chúng ta cần hiểu rõ nguyên lý hoạt động của thấu kính cũng như các đại lượng cần thiết để tính chiết suất.

Chiết suất (\(n\)) của một vật liệu được xác định bởi công thức:

Trong đó:

• \(v_{\text{chân không}}\) là vận tốc ánh sáng trong chân không (khoảng \(3 \times 10^8 \, \text{m/s}\)).
• \(v_{\text{vật liệu}}\) là vận tốc ánh sáng trong vật liệu mà chúng ta đang tính chiết suất.

Tuy nhiên, trong trường hợp của kính hiển vi, chúng ta thường tính chiết suất thông qua chỉ số khúc xạ của thấu kính, được xác định bằng công thức:

Trong đó:

• \(i\) là góc tới (góc giữa tia sáng tới và pháp tuyến của bề mặt thấu kính).
• \(r\) là góc khúc xạ (góc giữa tia sáng khúc xạ và pháp tuyến).

Các bước thực hiện:

1. Xác định góc tới \(i\) và góc khúc xạ \(r\) bằng cách quan sát thực nghiệm hoặc sử dụng các thông số đã biết từ bài toán.
2. Sử dụng công thức \(\sin i\) và \(\sin r\) để tính toán giá trị tương ứng.
3. Thay thế các giá trị này vào công thức trên để tìm ra chiết suất \(n\).
4. Đối chiếu kết quả với các giá trị chiết suất tiêu chuẩn của các vật liệu thường được sử dụng trong thấu kính kính hiển vi như thủy tinh, nhựa,... để kiểm tra độ chính xác.

Ví dụ: Giả sử một tia sáng đi từ không khí vào thấu kính thủy tinh trong kính hiển vi với góc tới \(i = 30^\circ\) và góc khúc xạ \(r = 20^\circ\). Chúng ta có thể tính toán như sau:

Kết quả này cho thấy chiết suất của thấu kính trong ví dụ là 1.46, khá gần với chiết suất tiêu chuẩn của thủy tinh là khoảng 1.5.

Bằng cách áp dụng các bước trên vào các bài tập thực hành, bạn có thể thành thạo kỹ năng tính toán chiết suất và hiểu sâu hơn về nguyên lý hoạt động của các thấu kính trong kính hiển vi.

Khi một tia sáng đi qua lăng kính, nó sẽ bị lệch hướng do sự thay đổi tốc độ ánh sáng khi di chuyển từ môi trường không khí vào môi trường lăng kính và ngược lại. Bài tập này sẽ giúp bạn tính toán và phân tích góc lệch của tia sáng khi đi qua lăng kính.

1. Góc Tới (i₁) và Góc Khúc Xạ (r₁):

   Góc tới là góc giữa tia sáng tới và pháp tuyến tại điểm tới trên mặt của lăng kính. Từ công thức khúc xạ ánh sáng, ta có:

   \[
   \sin i_1 = n \cdot \sin r_1
   \]

   Trong đó:
   

   
   
   • \(i_1\): góc tới.
   
   
   • \(r_1\): góc khúc xạ tại mặt đầu tiên.
   
   
   • \(n\): chiết suất của lăng kính.
   
   
   
   


2. Góc Khúc Xạ (r₂) tại Mặt Thứ Hai:

   Sau khi tia sáng đi qua mặt đầu tiên, nó sẽ tới mặt bên thứ hai của lăng kính với góc tới mới \(r_2\). Tương tự, góc khúc xạ tại mặt thứ hai được tính bằng công thức:

   \[
   \sin i_2 = n \cdot \sin r_2
   \]

3. Góc Ở Đỉnh (A):

   Góc ở đỉnh của lăng kính là góc giữa hai mặt bên của lăng kính, được tính bằng:

   \[
   A = r_1 + r_2
   \]

4. Góc Lệch (D):

   Góc lệch là góc giữa tia sáng tới và tia sáng ló ra khỏi lăng kính. Công thức tính góc lệch:

   \[
   D = i_1 + i_2 - A
   \]

   Góc lệch phụ thuộc vào góc tới, chiết suất của lăng kính và góc ở đỉnh của lăng kính.

Như vậy, bằng cách sử dụng các công thức trên, ta có thể phân tích và tính toán chính xác góc lệch của tia sáng khi đi qua lăng kính, từ đó hiểu rõ hơn về hiện tượng khúc xạ ánh sáng qua các dụng cụ quang học như lăng kính.

Trong bài tập này, chúng ta sẽ tìm hiểu cách tính góc nhìn của vật khi quan sát qua kính lúp. Kính lúp là một dụng cụ quang học phổ biến, được sử dụng để quan sát các vật nhỏ bằng cách phóng đại hình ảnh của chúng.

Bước 1: Xác định thông số của kính lúp

Kính lúp có độ phóng đại \( G \), được xác định bởi công thức:

\[ G = \frac{Đ}{f} \]

Trong đó:

• \( Đ \) là khoảng cực cận của mắt người quan sát (thường là 25 cm).
• \( f \) là tiêu cự của kính lúp.

Bước 2: Tính góc nhìn qua kính lúp

Khi quan sát vật qua kính lúp, góc nhìn của vật có thể tính theo công thức:

\[ \alpha = \frac{h}{f} \]

Trong đó:

• \( h \) là chiều cao của vật cần quan sát.
• \( f \) là tiêu cự của kính lúp.

Góc nhìn của vật sẽ tăng lên khi chiều cao của vật hoặc khi tiêu cự của kính lúp giảm.

Bước 3: Trường hợp ngắm chừng ở vô cực

Khi mắt không phải điều tiết, tức là ngắm chừng ở vô cực, độ bội giác của kính lúp \( G_{\infty} \) được tính như sau:

\[ G_{\infty} = \frac{Đ}{f} \]

Giá trị của \( G_{\infty} \) phụ thuộc vào kính lúp và thường dao động từ 2,5 đến 25 lần.

Kết luận

Việc tính góc nhìn qua kính lúp giúp chúng ta hiểu rõ hơn về cách hoạt động của kính lúp và làm sao để tối ưu hóa việc quan sát các vật nhỏ. Để đạt được góc nhìn tốt nhất, người sử dụng cần chọn loại kính lúp có độ phóng đại và tiêu cự phù hợp với nhu cầu của mình.

Trong bài tập này, chúng ta sẽ tính toán khoảng cách từ vật đến thấu kính trong kính cận. Đây là một bước quan trọng để xác định vị trí của ảnh và cách mà kính cận điều chỉnh tật khúc xạ của mắt.

Công thức cơ bản:

Để tính khoảng cách từ vật đến thấu kính trong kính cận, chúng ta có thể sử dụng công thức sau:

Trong đó:

• \(f\): Tiêu cự của thấu kính.
• \(d_o\): Khoảng cách từ vật đến thấu kính.
• \(d_i\): Khoảng cách từ ảnh đến thấu kính (trong trường hợp kính cận, ảnh thường được đặt tại điểm cực viễn của mắt).

Quy trình tính toán:

1. Xác định tiêu cự: Đầu tiên, chúng ta cần biết tiêu cự của thấu kính trong kính cận. Thông thường, tiêu cự này có giá trị âm vì thấu kính cận là thấu kính phân kỳ.
2. Áp dụng công thức: Sử dụng công thức \(\frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i}\) để tìm giá trị của \(d_o\).
3. Tính toán: Giải phương trình để tìm ra khoảng cách từ vật đến thấu kính.

Ví dụ minh họa:

Giả sử kính cận có tiêu cự \(f = -20 \, cm\) và điểm cực viễn của mắt là \(d_i = -30 \, cm\). Chúng ta có thể tính được khoảng cách từ vật đến thấu kính như sau:

Giải phương trình này, ta có:

Do đó, khoảng cách từ vật đến thấu kính:

Kết quả này cho thấy vật nằm ở khoảng cách 60 cm trước thấu kính để tạo ra ảnh tại điểm cực viễn của mắt.

Với cách tiếp cận này, chúng ta có thể xác định chính xác khoảng cách cần thiết để điều chỉnh tật khúc xạ bằng kính cận.