Lực Tương Tác Giữa Hai Điện Tích Trong Chân Không: Khám Phá Sức Mạnh Vô Hình

Lực tương tác giữa hai điện tích trong chân không là một trong những khái niệm cơ bản trong vật lý điện từ. Lực này tuân theo định luật Coulomb, mô tả mối quan hệ giữa hai điện tích điểm và khoảng cách giữa chúng. Cụ thể, lực tương tác tỉ lệ thuận với tích của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

1. Định luật Coulomb

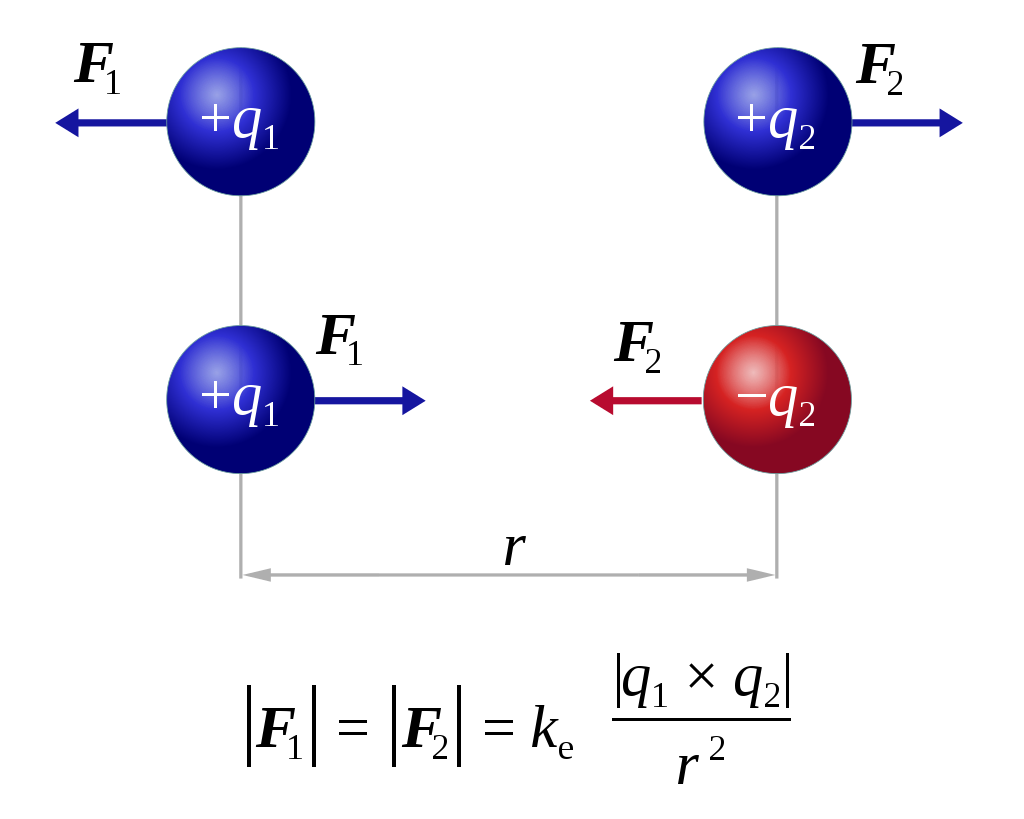
Theo định luật Coulomb, lực tương tác giữa hai điện tích điểm trong chân không được xác định bởi công thức:

\[
F = k \cdot \frac{|q_1 \cdot q_2|}{r^2}
\]

Trong đó:

• \( F \) là độ lớn của lực tương tác (Newton).
• \( k \) là hằng số Coulomb, \( k \approx 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \).
• \( q_1 \) và \( q_2 \) là độ lớn của hai điện tích (Coulomb).
• \( r \) là khoảng cách giữa hai điện tích (mét).

2. Đặc điểm của lực tương tác

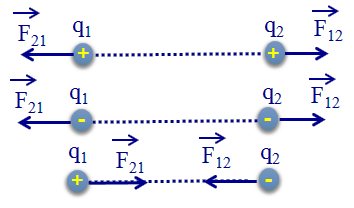
• Lực tương tác giữa hai điện tích cùng dấu là lực đẩy.
• Lực tương tác giữa hai điện tích trái dấu là lực hút.
• Phương của lực tương tác nằm dọc theo đường thẳng nối hai điện tích.

3. Ảnh hưởng của môi trường

Khi có sự hiện diện của một môi trường khác (như nước, không khí) giữa hai điện tích, hằng số điện môi của môi trường sẽ ảnh hưởng đến độ lớn của lực tương tác. Trong chân không, hằng số điện môi là 1, nhưng trong các môi trường khác, giá trị này có thể lớn hơn, làm giảm lực tương tác.

4. Ứng dụng của định luật Coulomb

• Xác định lực tương tác giữa các hạt mang điện trong vật liệu điện môi.
• Dự đoán sự phân bố điện tích trên bề mặt các vật dẫn.
• Tính toán lực giữa các hạt trong các hệ thống điện từ phức tạp.

5. Ví dụ minh họa

Giả sử có hai điện tích \( q_1 = 2 \, \text{C} \) và \( q_2 = -3 \, \text{C} \), đặt cách nhau 0,5 m trong chân không. Lực tương tác giữa chúng được tính như sau:

\[
F = 9 \times 10^9 \times \frac{|2 \times (-3)|}{0,5^2} = 2,16 \times 10^{11} \, \text{N}
\]

Lực này là lực hút do hai điện tích trái dấu.

6. Kết luận

Định luật Coulomb và các nguyên lý cơ bản về lực tương tác giữa các điện tích trong chân không không chỉ quan trọng trong nghiên cứu vật lý cơ bản mà còn có nhiều ứng dụng trong các lĩnh vực công nghệ và khoa học khác. Hiểu rõ về lực tương tác này giúp chúng ta dự đoán và giải thích nhiều hiện tượng tự nhiên cũng như ứng dụng trong đời sống hàng ngày.

Lực tương tác giữa hai điện tích trong chân không là một hiện tượng cơ bản trong vật lý, được mô tả bởi định luật Coulomb. Lực này tồn tại giữa hai điện tích điểm và là cơ sở để hiểu rõ hơn về các hiện tượng điện từ trong tự nhiên.

Định luật Coulomb phát biểu rằng lực tương tác giữa hai điện tích tỉ lệ thuận với tích của độ lớn hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng:

\[
F = k \cdot \frac{|q_1 \cdot q_2|}{r^2}
\]

Trong đó:

• \( F \) là lực tương tác (Newton).
• \( k \) là hằng số Coulomb, với giá trị xấp xỉ \( 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \).
• \( q_1 \) và \( q_2 \) là độ lớn của hai điện tích (Coulomb).
• \( r \) là khoảng cách giữa hai điện tích (mét).

Lực tương tác giữa hai điện tích có thể là lực hút hoặc lực đẩy, tùy thuộc vào dấu của các điện tích:

• Hai điện tích cùng dấu sẽ đẩy nhau.
• Hai điện tích trái dấu sẽ hút nhau.

Lực này không chỉ tồn tại trong chân không mà còn ảnh hưởng bởi môi trường xung quanh, tuy nhiên, trong chân không, các tính toán lực được đơn giản hóa và dễ hiểu hơn, giúp chúng ta nắm vững các nguyên lý cơ bản về tương tác điện từ.

Để tính toán lực tương tác giữa hai điện tích trong chân không, chúng ta sử dụng công thức định luật Coulomb, mô tả mối quan hệ giữa lực và các yếu tố liên quan:

\[
F = k \cdot \frac{|q_1 \cdot q_2|}{r^2}
\]

Trong đó:

• \( F \): Lực tương tác giữa hai điện tích, được đo bằng Newton (N).
• \( k \): Hằng số Coulomb, có giá trị xấp xỉ \( 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \).
• \( q_1 \) và \( q_2 \): Độ lớn của hai điện tích, được đo bằng Coulomb (C).
• \( r \): Khoảng cách giữa hai điện tích, được đo bằng mét (m).

Công thức này cho thấy rằng lực tương tác tỉ lệ thuận với tích của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng. Điều này có nghĩa là:

• Khi khoảng cách giữa hai điện tích tăng, lực tương tác sẽ giảm.
• Khi độ lớn của một trong hai điện tích tăng, lực tương tác sẽ tăng.

Đây là công thức cơ bản để xác định lực tương tác giữa hai điện tích trong bất kỳ môi trường nào, đặc biệt là trong chân không, nơi các yếu tố ảnh hưởng như hằng số điện môi không thay đổi.

Lực tương tác giữa hai điện tích trong chân không có một số đặc điểm quan trọng cần lưu ý, giúp chúng ta hiểu rõ hơn về bản chất và cách thức hoạt động của hiện tượng này.

• 1. Lực tỉ lệ thuận với tích độ lớn của hai điện tích:

  Lực tương tác giữa hai điện tích tăng lên khi độ lớn của một trong hai điện tích hoặc cả hai đều tăng. Điều này có nghĩa là nếu hai điện tích có độ lớn càng lớn, lực tương tác giữa chúng sẽ càng mạnh.

• 2. Lực tỉ lệ nghịch với bình phương khoảng cách:

  Khoảng cách giữa hai điện tích càng lớn, lực tương tác giữa chúng càng giảm. Cụ thể, khi khoảng cách giữa hai điện tích tăng gấp đôi, lực tương tác sẽ giảm đi bốn lần.

• 3. Lực tương tác phụ thuộc vào môi trường:

  Mặc dù công thức Coulomb áp dụng cho chân không, lực tương tác giữa hai điện tích cũng chịu ảnh hưởng bởi môi trường xung quanh, đặc biệt là hằng số điện môi của môi trường.

• 4. Lực tương tác có tính chất véc-tơ:

  Lực tương tác giữa hai điện tích có phương nằm trên đường nối hai điện tích và chiều phụ thuộc vào dấu của chúng: cùng dấu thì đẩy nhau, trái dấu thì hút nhau.

• 5. Tác động qua khoảng cách:

  Lực tương tác này có tác dụng ngay lập tức qua khoảng cách, dù hai điện tích có thể cách xa nhau trong không gian nhưng lực vẫn được truyền tải một cách trực tiếp.

Những đặc điểm này giúp chúng ta hiểu rõ hơn về cách thức các điện tích tương tác trong các hệ thống vật lý và ứng dụng trong nhiều lĩnh vực khác nhau của khoa học và công nghệ.

Lực tương tác giữa hai điện tích không chỉ phụ thuộc vào độ lớn và khoảng cách giữa chúng, mà còn bị ảnh hưởng bởi môi trường xung quanh. Môi trường này đóng vai trò quan trọng trong việc điều chỉnh và làm thay đổi cường độ của lực tương tác.

• 1. Hằng số điện môi của môi trường:

  Khi hai điện tích nằm trong một môi trường có hằng số điện môi $\varepsilon$, lực tương tác giữa chúng sẽ giảm đi so với khi ở trong chân không. Lực tương tác $F$ trong môi trường sẽ được tính theo công thức:

  $$
  
  F
  =
  
  
  k
  ·
  
  q
  1
  
  ·
  
  q
  2
  
  
  
  ε
  ·
  
  r
  2
  
  
  
  
  

  Ở đây, $k$ là hằng số Coulomb, $q_1$ và $q_2$ là độ lớn của hai điện tích, $r$ là khoảng cách giữa chúng, và $\varepsilon$ là hằng số điện môi của môi trường.

• 2. Môi trường đồng nhất và không đồng nhất:

  Trong môi trường đồng nhất, lực tương tác giữa hai điện tích được phân bố đều và không bị thay đổi theo vị trí. Tuy nhiên, trong môi trường không đồng nhất, sự phân bố của hằng số điện môi không đều có thể dẫn đến sự biến đổi không đồng nhất của lực tương tác.

• 3. Ảnh hưởng của các yếu tố vật lý khác:

  Nhiệt độ, áp suất, và sự hiện diện của các hạt khác trong môi trường cũng có thể ảnh hưởng đến lực tương tác giữa hai điện tích. Chẳng hạn, nhiệt độ cao có thể làm giảm độ nhớt của môi trường, từ đó ảnh hưởng đến sự truyền dẫn của lực tương tác.

• 4. Ứng dụng thực tiễn:

  Hiểu được ảnh hưởng của môi trường đến lực tương tác giữa hai điện tích là rất quan trọng trong các ứng dụng thực tiễn như thiết kế vật liệu cách điện, nghiên cứu tính chất điện của chất lỏng và khí, và trong công nghệ điện tử hiện đại.

Từ những đặc điểm này, chúng ta có thể thấy rằng môi trường không chỉ là một yếu tố thụ động, mà còn đóng vai trò quan trọng trong việc điều chỉnh và kiểm soát lực tương tác giữa các điện tích.

Qua các phân tích về lực tương tác giữa hai điện tích trong chân không, chúng ta có thể thấy rằng định luật Coulomb đóng vai trò cực kỳ quan trọng trong việc hiểu rõ bản chất của lực điện. Định luật này không chỉ giúp chúng ta tính toán lực tương tác giữa các điện tích mà còn là nền tảng cho nhiều lĩnh vực nghiên cứu và ứng dụng thực tiễn trong công nghệ.

6.1 Tổng kết lý thuyết về lực tương tác

Lực tương tác giữa hai điện tích tĩnh trong chân không có độ lớn tỉ lệ thuận với tích các độ lớn của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng. Đặc điểm này không chỉ áp dụng trong môi trường chân không mà còn có thể được điều chỉnh để phù hợp với các môi trường khác bằng cách thay đổi hằng số điện môi.

Định luật Coulomb cung cấp một cách tiếp cận đơn giản nhưng hiệu quả để mô tả lực điện trong nhiều hệ thống vật lý. Từ việc phân tích các tương tác tĩnh điện đơn giản, chúng ta có thể mở rộng hiểu biết về các hiện tượng phức tạp hơn như điện trường, điện thế và các lực tương tác trong các hệ thống đa điện tích.

6.2 Ứng dụng trong nghiên cứu và công nghệ

Nhờ vào định luật Coulomb, các nhà khoa học và kỹ sư đã phát triển nhiều ứng dụng công nghệ quan trọng. Ví dụ, lực tương tác giữa các điện tích là cơ sở cho hoạt động của các thiết bị điện tử như tụ điện, điện trở, và các linh kiện bán dẫn. Bên cạnh đó, trong lĩnh vực y sinh, định luật này được sử dụng để thiết kế và cải tiến các thiết bị chẩn đoán hình ảnh như MRI và các công nghệ chụp ảnh khác.

Trong nghiên cứu khoa học, định luật Coulomb tiếp tục đóng vai trò quan trọng trong việc khám phá các hiện tượng mới, đặc biệt trong vật lý hạt và nghiên cứu về vật liệu mới. Việc hiểu rõ và áp dụng định luật Coulomb giúp chúng ta dự đoán và kiểm soát các tương tác điện trong các hệ thống phức tạp, từ đó tạo ra những đột phá công nghệ có thể cải thiện chất lượng cuộc sống và mở rộng tri thức nhân loại.