Lực Tương Tác Điện Giữa Hai Điện Tích: Khái Niệm, Định Luật và Ứng Dụng Thực Tế

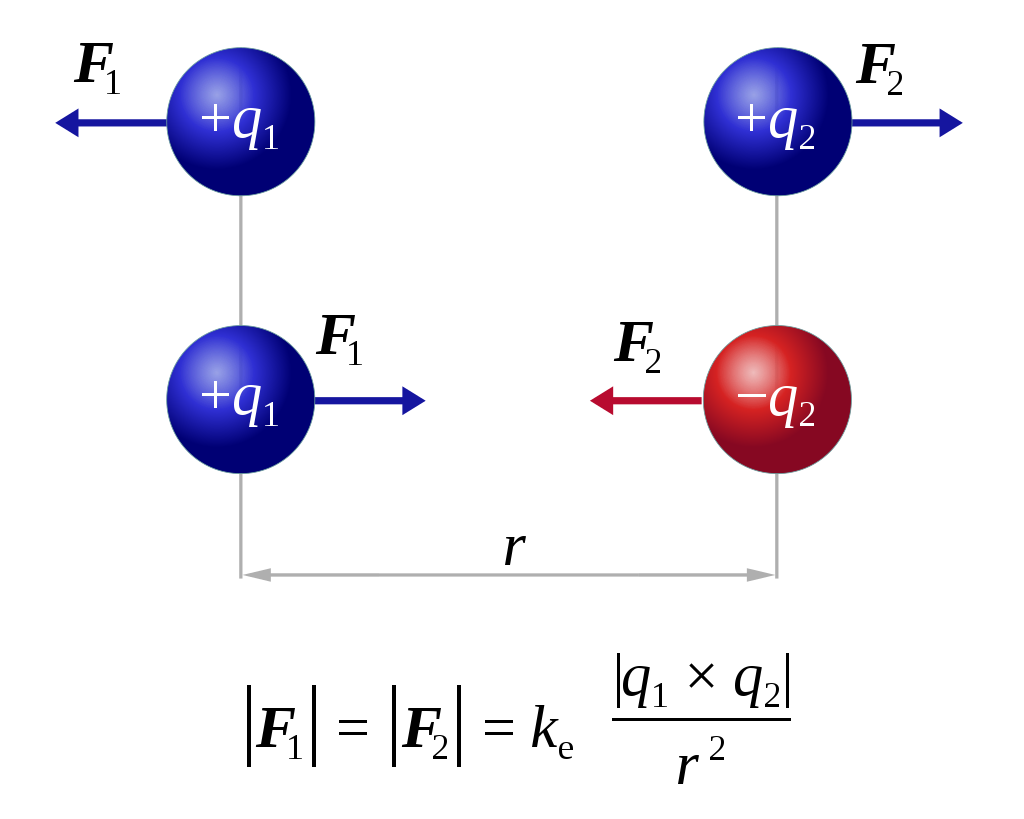
Lực tương tác điện giữa hai điện tích là một khái niệm quan trọng trong điện học, thường được mô tả bởi định luật Coulomb. Định luật này phát biểu rằng lực tương tác giữa hai điện tích điểm có phương trùng với đường thẳng nối hai điện tích và độ lớn của lực tỉ lệ thuận với tích giá trị tuyệt đối của hai điện tích, đồng thời tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

Công Thức Tính Lực Tương Tác Điện

Công thức tính lực tương tác điện giữa hai điện tích điểm được biểu diễn như sau:

Trong đó:

• \(F\): là độ lớn của lực tương tác (N).
• \(q_1, q_2\): là độ lớn của hai điện tích (C).
• \(r\): là khoảng cách giữa hai điện tích (m).
• \(k\): là hằng số tỉ lệ, phụ thuộc vào môi trường giữa hai điện tích.

Đặc Điểm Của Lực Tương Tác Điện

• Hai điện tích cùng dấu sẽ đẩy nhau, trong khi hai điện tích trái dấu sẽ hút nhau.
• Lực tương tác giữa hai điện tích có phương nằm trên đường thẳng nối giữa chúng.
• Khi đặt các điện tích trong chân không, hằng số \(k\) được tính bằng \( k = \frac{1}{4\pi\varepsilon_0} \), với \(\varepsilon_0\) là hằng số điện môi của chân không, có giá trị \(\varepsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{N} \cdot \text{m}^2\).

Ảnh Hưởng Của Môi Trường

Lực tương tác giữa hai điện tích sẽ thay đổi phụ thuộc vào môi trường mà chúng được đặt trong. Hằng số điện môi \(\varepsilon\) của môi trường ảnh hưởng trực tiếp đến giá trị của lực tương tác. Khi đặt trong một môi trường có hằng số điện môi \(\varepsilon\), lực tương tác sẽ giảm đi \(\varepsilon\) lần so với trong chân không:

Ứng Dụng Thực Tiễn

Trong thực tế, định luật Coulomb được áp dụng rộng rãi trong việc tính toán và phân tích các hệ thống điện tích trong các ngành vật lý và kỹ thuật điện. Nó cũng giúp giải quyết các bài toán liên quan đến lực tương tác giữa các điện tích trong môi trường khác nhau, chẳng hạn như trong chất cách điện hay trong các vật liệu có điện môi khác nhau.

Lực tương tác điện là một trong những hiện tượng cơ bản trong vật lý, đóng vai trò quan trọng trong nhiều lĩnh vực của khoa học và cuộc sống. Lực này mô tả sự tác động qua lại giữa hai điện tích điểm, thể hiện qua lực hút hoặc đẩy tùy thuộc vào dấu của điện tích. Được phát biểu bởi định luật Coulomb, lực tương tác giữa hai điện tích tỉ lệ thuận với tích độ lớn của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng. Hiểu rõ lực tương tác điện giúp chúng ta giải thích được nhiều hiện tượng tự nhiên cũng như ứng dụng trong công nghệ và đời sống.

Định luật Cu-lông mô tả lực tương tác giữa hai điện tích điểm trong môi trường chân không. Theo định luật này, lực tương tác giữa hai điện tích có phương trùng với đường thẳng nối hai điện tích và có độ lớn tỉ lệ thuận với tích của hai điện tích, đồng thời tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

Công thức của định luật Cu-lông được biểu diễn dưới dạng:

Trong đó:

• \(F\) là độ lớn của lực tương tác điện (đơn vị: Newton, N).
• \(q_1\) và \(q_2\) là độ lớn của hai điện tích (đơn vị: Coulomb, C).
• \(r\) là khoảng cách giữa hai điện tích (đơn vị: mét, m).
• \(k\) là hằng số Coulomb, có giá trị \(k \approx 9 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2\).

Định luật Cu-lông không chỉ có ý nghĩa quan trọng trong lý thuyết, mà còn có nhiều ứng dụng thực tế, từ việc giải thích các hiện tượng tĩnh điện cho đến việc thiết kế các thiết bị điện tử, hệ thống truyền tải điện năng, và nhiều lĩnh vực khác.

Lực tương tác điện giữa hai điện tích không chỉ phụ thuộc vào giá trị của các điện tích mà còn bị ảnh hưởng bởi nhiều yếu tố khác. Hiểu rõ những yếu tố này giúp giải thích được các hiện tượng điện từ trong đời sống và ứng dụng kỹ thuật.

• Khoảng cách giữa các điện tích: Theo định luật Cu-lông, lực tương tác điện tỉ lệ nghịch với bình phương khoảng cách giữa hai điện tích. Nghĩa là, khi khoảng cách tăng lên gấp đôi, lực sẽ giảm đi 4 lần, biểu diễn qua công thức \[F = \dfrac{k \cdot |q_1 \cdot q_2|}{r^2}\].
• Độ lớn của điện tích: Lực tương tác tỉ lệ thuận với độ lớn của các điện tích. Khi một trong hai điện tích tăng lên, lực tương tác cũng sẽ tăng tương ứng.
• Môi trường xung quanh: Hằng số điện môi của môi trường ảnh hưởng đến lực tương tác giữa các điện tích. Môi trường với hằng số điện môi cao sẽ làm giảm lực tương tác điện, so với môi trường chân không (với hằng số điện môi là 1).
• Hình dạng và kích thước của các vật thể: Nếu các điện tích không phải là điểm mà có kích thước đáng kể, phân bố điện tích và hình dạng của các vật thể có thể ảnh hưởng đến cách lực tương tác biểu hiện.

Những yếu tố trên là nền tảng để hiểu sâu hơn về các hiện tượng điện từ trong tự nhiên cũng như trong các ứng dụng kỹ thuật.

Trong vật lý, lực Cu-lông và lực hấp dẫn là hai lực cơ bản có vai trò quan trọng trong các hiện tượng tự nhiên. Tuy nhiên, chúng khác nhau về bản chất và cách thức hoạt động.

• Giống nhau:
• Cả hai lực đều tuân theo quy luật nghịch đảo bình phương khoảng cách, tức là độ lớn của lực giảm dần khi khoảng cách giữa hai đối tượng tăng lên.
• Đều là lực tác dụng từ xa, không cần tiếp xúc trực tiếp giữa các vật thể.
• Khác nhau:
• Bản chất: Lực Cu-lông là lực điện từ, tác dụng giữa các điện tích. Lực hấp dẫn là lực cơ học, tác dụng giữa các khối lượng.
• Độ lớn: Lực Cu-lông thường mạnh hơn rất nhiều so với lực hấp dẫn. Ví dụ, lực Cu-lông giữa hai electron lớn hơn lực hấp dẫn giữa chúng khoảng \[10^{39}\] lần.
• Phương thức tác dụng: Lực Cu-lông có thể là lực hút hoặc lực đẩy tùy thuộc vào dấu của điện tích, trong khi lực hấp dẫn luôn là lực hút.

Để hiểu rõ hơn về lực tương tác điện giữa hai điện tích, chúng ta sẽ cùng xem qua một số ví dụ và bài tập minh họa dưới đây.

• Bài tập 1: Hai điện tích điểm \( q_1 = 3 \times 10^{-8} C \) và \( q_2 = 2 \times 10^{-8} C \) được đặt tại hai điểm A và B trong chân không với khoảng cách \( AB = 5 \, cm \). Hãy tính lực tương tác giữa hai điện tích này.

Giải: Ta sử dụng công thức Coulomb:

\[ F = k \times \frac{{|q_1 \times q_2|}}{{r^2}} \]

Với \( k = 9 \times 10^9 \, Nm^2/C^2 \), thay số vào ta được:

\[ F = 9 \times 10^9 \times \frac{{3 \times 10^{-8} \times 2 \times 10^{-8}}}{{0,05^2}} \approx 2,16 \times 10^{-3} \, N \]
• Bài tập 2: Trong một môi trường có hằng số điện môi \( \varepsilon = 81 \), có ba quả cầu nhỏ mang các điện tích \( q_1 = 6 \times 10^{-7} C \), \( q_2 = 2 \times 10^{-7} C \), và \( q_3 = 10^{-6} C \), đặt trên một đường thẳng với khoảng cách \( r_{12} = 40 \, cm \) và \( r_{23} = 60 \, cm \). Hãy xác định lực tương tác tổng hợp tác dụng lên mỗi quả cầu.

Giải: Tính lần lượt các lực tương tác giữa từng cặp điện tích và tổng hợp các lực này theo quy tắc hình học để tìm ra lực tác dụng tổng hợp lên mỗi quả cầu.

• Bài tập 3: Hai điện tích \( q_1 = 8 \times 10^{-8} C \) và \( q_2 = -8 \times 10^{-8} C \) được đặt tại các điểm A và B trong không khí, với khoảng cách \( AB = 10 \, cm \). Điện tích \( q_3 = 8 \times 10^{-8} C \) được đặt tại điểm C sao cho \( CA = 4 \, cm \) và \( CB = 6 \, cm \). Hãy tính lực tác dụng lên \( q_3 \).

Giải: Sử dụng nguyên lý chồng chất lực để tính toán các lực tác dụng lên \( q_3 \) từ \( q_1 \) và \( q_2 \), sau đó tổng hợp để tìm ra lực cuối cùng.

Lực tương tác điện giữa hai điện tích là một khái niệm cơ bản trong vật lý, được thể hiện rõ qua định luật Cu-lông. Thông qua bài viết này, chúng ta đã khám phá cách lực này phụ thuộc vào độ lớn của điện tích và khoảng cách giữa chúng. Hiểu biết về lực tương tác điện không chỉ giúp giải thích các hiện tượng trong phòng thí nghiệm mà còn có ứng dụng rộng rãi trong các lĩnh vực công nghệ và đời sống. Nhờ đó, chúng ta có thể phát triển những giải pháp hiệu quả trong công nghệ điện tử, viễn thông, và nhiều lĩnh vực khác.