Chủ đề xác định lực tương tác giữa 2 điện tích: Bài viết này sẽ giúp bạn hiểu rõ cách xác định lực tương tác giữa hai điện tích thông qua định luật Cu-lông, các yếu tố ảnh hưởng, và ứng dụng thực tế trong đời sống. Hãy cùng khám phá các ví dụ cụ thể và bài tập vận dụng để củng cố kiến thức một cách hiệu quả nhất.
Mục lục
- Xác định lực tương tác giữa hai điện tích
- 1. Tổng quan về lực tương tác giữa hai điện tích
- 2. Ứng dụng định luật Cu-lông trong tính toán lực tương tác
- 3. So sánh lực tương tác giữa các điện tích trong các môi trường khác nhau
- 4. Bài tập vận dụng định luật Cu-lông
- 5. Ứng dụng của lực tương tác giữa các điện tích trong đời sống
- 6. Kết luận
Xác định lực tương tác giữa hai điện tích
Để xác định lực tương tác giữa hai điện tích, ta sử dụng Định luật Cu-lông. Định luật này phát biểu rằng lực tương tác tĩnh điện giữa hai điện tích điểm trong chân không có phương nằm trên đường thẳng nối hai điện tích và có độ lớn tỉ lệ thuận với tích độ lớn của hai điện tích, đồng thời tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
Công thức xác định lực tương tác
Lực tương tác giữa hai điện tích được tính theo công thức:
Trong đó:
- \( F \) là độ lớn của lực tương tác giữa hai điện tích (N).
- \( q_1, q_2 \) là độ lớn của các điện tích (Coulomb).
- \( r \) là khoảng cách giữa hai điện tích (m).
- \( k \) là hằng số Cu-lông, có giá trị \( k = 9 \times 10^9 \, \text{N}\cdot\text{m}^2/\text{C}^2 \) trong chân không.
Ví dụ minh họa
Giả sử có hai điện tích \( q_1 = 2 \times 10^{-6} \, \text{C} \) và \( q_2 = -3 \times 10^{-6} \, \text{C} \) đặt cách nhau 10 cm trong không khí. Lực tương tác giữa chúng được tính như sau:
Vì hai điện tích mang dấu trái nhau, nên lực tương tác giữa chúng là lực hút.
Tính chất của lực tương tác giữa hai điện tích
- Lực tương tác giữa hai điện tích là lực hấp dẫn nếu chúng mang điện tích trái dấu, và là lực đẩy nếu chúng mang điện tích cùng dấu.
- Lực này có phương nằm trên đường thẳng nối hai điện tích.
- Trong môi trường có hằng số điện môi \( \varepsilon \), độ lớn của lực tương tác sẽ giảm đi theo tỷ lệ \( 1/\varepsilon \).
Ví dụ, nếu hai điện tích được đặt trong môi trường dầu với hằng số điện môi \( \varepsilon = 2 \), lực tương tác giữa chúng sẽ giảm đi một nửa so với khi đặt trong không khí.
Ứng dụng thực tế
Định luật Cu-lông không chỉ là nền tảng lý thuyết trong vật lý học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực như điện tử, công nghệ thông tin, và kỹ thuật viễn thông.
.png)
1. Tổng quan về lực tương tác giữa hai điện tích
Lực tương tác giữa hai điện tích là một hiện tượng vật lý cơ bản, đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật. Khi hai vật mang điện tích tiếp xúc hoặc đặt gần nhau, chúng sẽ tác dụng lực lên nhau. Lực này có thể là lực hút hoặc lực đẩy, tùy thuộc vào dấu của các điện tích.
Theo Định luật Cu-lông, lực tương tác giữa hai điện tích điểm trong chân không được mô tả bằng công thức:
Trong đó:
- \( F \) là độ lớn của lực tương tác (N).
- \( q_1 \) và \( q_2 \) là độ lớn của hai điện tích (Coulomb).
- \( r \) là khoảng cách giữa hai điện tích (m).
- \( k \) là hằng số điện \( k = 9 \times 10^9 \, \text{N}\cdot\text{m}^2/\text{C}^2 \).
Lực tương tác giữa hai điện tích có các đặc điểm sau:
- Phương và chiều của lực: Lực tương tác có phương nằm trên đường thẳng nối hai điện tích. Nếu hai điện tích cùng dấu, lực sẽ đẩy, ngược lại nếu khác dấu, lực sẽ hút.
- Độ lớn của lực: Độ lớn của lực tỉ lệ thuận với tích của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
- Ảnh hưởng của môi trường: Trong môi trường có hằng số điện môi \( \varepsilon \), lực tương tác sẽ giảm đi theo công thức: \[ F = \frac{1}{4\pi\varepsilon} \cdot \frac{|q_1 \cdot q_2|}{r^2} \]
Việc hiểu rõ và áp dụng chính xác định luật Cu-lông không chỉ giúp giải quyết các bài toán vật lý mà còn có ứng dụng rộng rãi trong các lĩnh vực như điện tử, viễn thông, và công nghệ cao.
2. Ứng dụng định luật Cu-lông trong tính toán lực tương tác
Định luật Cu-lông không chỉ là cơ sở lý thuyết quan trọng trong vật lý mà còn được ứng dụng rộng rãi trong việc tính toán lực tương tác giữa các điện tích trong nhiều lĩnh vực khác nhau. Dưới đây là một số ứng dụng cụ thể của định luật Cu-lông trong các bài toán và thực tế.
- Tính toán lực tương tác giữa các điện tích điểm:
Trong các bài toán vật lý cơ bản, định luật Cu-lông được sử dụng để tính lực tương tác giữa hai điện tích điểm. Ví dụ, cho hai điện tích \( q_1 \) và \( q_2 \) đặt cách nhau khoảng cách \( r \), lực tương tác giữa chúng được xác định bằng công thức:
\[ F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \] - Tính toán lực trong các hệ thống nhiều điện tích:
Định luật Cu-lông cũng có thể được áp dụng để tính toán lực tương tác trong các hệ thống gồm nhiều điện tích. Trong trường hợp này, tổng lực tác dụng lên một điện tích sẽ là tổng vector của các lực do các điện tích khác tác dụng lên.
- Xác định lực tác dụng trong các môi trường khác nhau:
Định luật Cu-lông cũng được sử dụng để xác định lực tương tác giữa các điện tích trong các môi trường khác nhau. Khi đặt các điện tích trong một môi trường có hằng số điện môi \( \varepsilon \), công thức tính lực sẽ thay đổi thành:
\[ F = \frac{1}{4\pi\varepsilon} \cdot \frac{|q_1 \cdot q_2|}{r^2} \]Ví dụ, trong nước với hằng số điện môi lớn, lực tương tác sẽ giảm đi so với trong không khí hay chân không.
- Ứng dụng trong kỹ thuật điện và điện tử:
Trong các thiết bị điện tử, định luật Cu-lông được sử dụng để thiết kế và phân tích các hệ thống điện tích, đặc biệt trong việc xác định lực tác dụng giữa các thành phần nhỏ như trong mạch vi điện tử.
- Ứng dụng trong công nghệ y sinh và sinh học:
Trong y học, định luật Cu-lông được áp dụng để hiểu về tương tác giữa các phân tử mang điện trong cơ thể, chẳng hạn như tương tác giữa DNA và protein. Điều này đóng vai trò quan trọng trong việc nghiên cứu các quá trình sinh học và phát triển các phương pháp điều trị mới.
Việc nắm vững và ứng dụng linh hoạt định luật Cu-lông không chỉ giúp giải quyết các bài toán lý thuyết mà còn mở ra nhiều hướng nghiên cứu và phát triển công nghệ trong nhiều lĩnh vực khác nhau.

3. So sánh lực tương tác giữa các điện tích trong các môi trường khác nhau
Lực tương tác giữa hai điện tích không chỉ phụ thuộc vào độ lớn của các điện tích và khoảng cách giữa chúng, mà còn phụ thuộc vào môi trường mà chúng tồn tại. Môi trường có thể làm thay đổi đáng kể độ lớn của lực tương tác thông qua hằng số điện môi \( \varepsilon \). Dưới đây là sự so sánh lực tương tác giữa các điện tích trong các môi trường khác nhau.
- Trong chân không
Trong chân không, lực tương tác giữa hai điện tích được tính theo định luật Cu-lông với công thức chuẩn:
\[ F_{\text{chân không}} = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \]Trong đó, hằng số điện môi của chân không là \( \varepsilon_0 = 1 \). Điều này có nghĩa rằng, lực tương tác trong chân không là lớn nhất so với các môi trường khác.
- Trong không khí
Không khí có hằng số điện môi xấp xỉ \( \varepsilon_{\text{không khí}} = 1.0006 \), gần bằng với chân không, do đó lực tương tác giữa các điện tích trong không khí rất giống với trong chân không. Công thức tính lực tương tác trong không khí là:
\[ F_{\text{không khí}} \approx k \cdot \frac{|q_1 \cdot q_2|}{r^2} \] - Trong nước
Nước có hằng số điện môi rất lớn, khoảng \( \varepsilon_{\text{nước}} = 80 \). Do đó, lực tương tác giữa các điện tích trong nước sẽ giảm đáng kể so với trong chân không hoặc không khí. Công thức tính lực tương tác trong nước là:
\[ F_{\text{nước}} = \frac{1}{4\pi \varepsilon_{\text{nước}}} \cdot \frac{|q_1 \cdot q_2|}{r^2} \]Lực này chỉ bằng 1/80 lực trong chân không.
- Trong dầu
Dầu cũng có hằng số điện môi lớn, tuy nhiên nhỏ hơn nước, khoảng \( \varepsilon_{\text{dầu}} = 2-3 \). Lực tương tác giữa các điện tích trong dầu cũng sẽ giảm đi so với trong không khí hay chân không, nhưng không nhiều bằng trong nước. Công thức tính lực tương tác trong dầu là:
\[ F_{\text{dầu}} = \frac{1}{4\pi \varepsilon_{\text{dầu}}} \cdot \frac{|q_1 \cdot q_2|}{r^2} \]Lực này nhỏ hơn lực trong không khí khoảng 2-3 lần.
Tóm lại, lực tương tác giữa các điện tích giảm khi hằng số điện môi của môi trường tăng. Điều này cần được cân nhắc khi tính toán và ứng dụng lực điện trong các môi trường khác nhau, đặc biệt trong các ngành khoa học và công nghệ liên quan đến điện từ học.
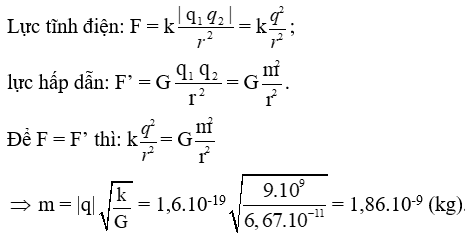
XEM THÊM:
4. Bài tập vận dụng định luật Cu-lông
Để hiểu rõ hơn về cách áp dụng định luật Cu-lông vào thực tế, dưới đây là một số bài tập tiêu biểu giúp bạn củng cố kiến thức và kỹ năng tính toán lực tương tác giữa hai điện tích.
- Bài tập 1: Xác định lực tương tác giữa hai điện tích điểm trong chân không
Giả sử có hai điện tích \( q_1 = 3 \times 10^{-6} \, \text{C} \) và \( q_2 = -2 \times 10^{-6} \, \text{C} \) đặt cách nhau \( r = 0.1 \, \text{m} \) trong chân không. Hãy xác định lực tương tác giữa hai điện tích này.
Giải: Áp dụng công thức định luật Cu-lông:
\[ F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \]Với \( k = 9 \times 10^9 \, \text{N}\cdot\text{m}^2/\text{C}^2 \), ta có:
\[ F = 9 \times 10^9 \cdot \frac{3 \times 10^{-6} \cdot 2 \times 10^{-6}}{(0.1)^2} = 5.4 \, \text{N} \]Do \( q_1 \) và \( q_2 \) có dấu trái ngược, nên đây là lực hút.
- Bài tập 2: Xác định khoảng cách giữa hai điện tích khi biết lực tương tác
Hai điện tích \( q_1 = 5 \times 10^{-7} \, \text{C} \) và \( q_2 = 8 \times 10^{-7} \, \text{C} \) đặt trong chân không, tạo ra lực đẩy \( F = 0.36 \, \text{N} \). Tìm khoảng cách \( r \) giữa hai điện tích.
Giải: Sử dụng công thức định luật Cu-lông:
\[ r = \sqrt{k \cdot \frac{|q_1 \cdot q_2|}{F}} \]Thay các giá trị đã biết:
\[ r = \sqrt{9 \times 10^9 \cdot \frac{5 \times 10^{-7} \cdot 8 \times 10^{-7}}{0.36}} = 0.05 \, \text{m} \] - Bài tập 3: Tính lực tương tác trong môi trường có hằng số điện môi
Hai điện tích \( q_1 = 1 \times 10^{-6} \, \text{C} \) và \( q_2 = 2 \times 10^{-6} \, \text{C} \) đặt cách nhau \( 0.2 \, \text{m} \) trong nước có hằng số điện môi \( \varepsilon = 80 \). Xác định lực tương tác giữa hai điện tích.
Giải: Trong môi trường có hằng số điện môi, lực được tính theo công thức:
\[ F = \frac{1}{4\pi\varepsilon} \cdot \frac{|q_1 \cdot q_2|}{r^2} \]Thay giá trị \( \varepsilon \) và các thông số khác:
\[ F = \frac{9 \times 10^9}{80} \cdot \frac{1 \times 10^{-6} \cdot 2 \times 10^{-6}}{(0.2)^2} = 0.1125 \, \text{N} \]
Các bài tập trên giúp làm rõ các khía cạnh quan trọng của định luật Cu-lông và cung cấp cơ hội để thực hành các kỹ năng tính toán cần thiết cho việc giải quyết các vấn đề liên quan đến lực tương tác giữa các điện tích.

5. Ứng dụng của lực tương tác giữa các điện tích trong đời sống
Lực tương tác giữa các điện tích không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng quan trọng trong đời sống hàng ngày. Dưới đây là một số ví dụ tiêu biểu về cách lực tương tác giữa các điện tích được sử dụng trong thực tế.
- Máy photocopy và máy in laser
Cả máy photocopy và máy in laser đều dựa trên nguyên lý của lực tĩnh điện. Trong quá trình hoạt động, một trống quang học được tích điện để thu hút các hạt mực (toner), sau đó mực được chuyển lên giấy thông qua lực tương tác giữa các điện tích, tạo nên hình ảnh hoặc văn bản.
- Máy lọc bụi tĩnh điện
Máy lọc bụi tĩnh điện được sử dụng để làm sạch không khí trong các hệ thống thông gió công nghiệp và dân dụng. Các hạt bụi trong không khí được tích điện và sau đó bị hút vào các tấm kim loại có điện tích trái dấu, giúp loại bỏ chúng khỏi không khí.
- Phun sơn tĩnh điện
Kỹ thuật phun sơn tĩnh điện sử dụng lực tương tác giữa các điện tích để sơn bám chắc vào bề mặt vật liệu. Sơn được tích điện trái dấu với vật liệu, giúp sơn trải đều và bám chặt hơn, tạo ra lớp sơn mịn màng và bền bỉ.
- Thiết bị chống sét
Các thiết bị chống sét hoạt động dựa trên nguyên lý của lực tương tác giữa các điện tích để giảm thiểu nguy cơ sét đánh vào các công trình. Bằng cách cân bằng điện tích trên bề mặt, các thiết bị này giúp hạn chế sự chênh lệch điện thế, từ đó giảm nguy cơ phát sinh tia sét.
- Thiết bị y tế: Máy sốc tim (Defibrillator)
Máy sốc tim sử dụng lực tương tác giữa các điện tích để tạo ra một dòng điện đủ mạnh nhằm khôi phục nhịp tim cho bệnh nhân. Điện tích được nạp vào và giải phóng nhanh chóng, tạo ra cú sốc điện tác động trực tiếp lên tim.
Những ứng dụng này minh chứng cho tầm quan trọng của lực tương tác giữa các điện tích trong nhiều lĩnh vực, từ công nghiệp, y tế cho đến đời sống hàng ngày, giúp cải thiện hiệu quả và chất lượng cuộc sống của con người.
6. Kết luận
Việc xác định lực tương tác giữa hai điện tích là một nguyên tắc cơ bản trong vật lý học, với ứng dụng rộng rãi từ lý thuyết đến thực tiễn. Qua bài viết này, chúng ta đã hiểu rõ về cách thức lực tương tác này hoạt động dựa trên định luật Cu-lông, cũng như những ứng dụng thiết thực trong đời sống hàng ngày, từ công nghiệp đến y tế.
Nhờ định luật Cu-lông, chúng ta có thể dự đoán và tính toán chính xác lực tương tác giữa các điện tích, từ đó phát triển các công nghệ tiên tiến như máy photocopy, máy lọc bụi tĩnh điện, và nhiều thiết bị quan trọng khác. Đồng thời, những kiến thức này cũng giúp chúng ta hiểu rõ hơn về thế giới tự nhiên và các hiện tượng xung quanh.
Cuối cùng, việc vận dụng hiệu quả lực tương tác giữa các điện tích không chỉ nâng cao hiệu quả sản xuất và cải thiện chất lượng cuộc sống mà còn mở ra nhiều hướng đi mới trong nghiên cứu và phát triển công nghệ.



















