Hợp Lực Hai Lực Song Song: Tìm Hiểu Toàn Diện Về Quy Tắc Vật Lý Quan Trọng Này

Trong vật lý, "hợp lực hai lực song song" là một khái niệm quan trọng liên quan đến cơ học, đặc biệt trong việc tính toán lực tổng hợp từ hai lực song song tác động lên một vật thể. Khái niệm này không chỉ có ý nghĩa lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống.

1. Khái Niệm Về Hợp Lực Hai Lực Song Song

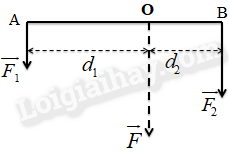
Hợp lực của hai lực song song là một lực duy nhất thay thế hai lực này, có giá trị, phương và chiều xác định dựa trên các lực thành phần. Trong đó:

• Hợp lực: Lực tổng hợp từ hai lực song song, có độ lớn bằng tổng hoặc hiệu của các độ lớn của hai lực thành phần tùy vào chiều của chúng.
• Phương: Hợp lực có phương song song với phương của hai lực thành phần.
• Chiều: Chiều của hợp lực phụ thuộc vào chiều của các lực thành phần.

2. Quy Tắc Tổng Hợp Hai Lực Song Song

Có hai quy tắc chính khi tổng hợp hai lực song song: cùng chiều và ngược chiều.

2.1. Hợp Lực Song Song Cùng Chiều

Nếu hai lực song song và cùng chiều, hợp lực sẽ có độ lớn bằng tổng độ lớn của hai lực:

\[ F = F_1 + F_2 \]

Giá của hợp lực sẽ chia khoảng cách giữa hai giá của hai lực thành phần theo tỉ lệ nghịch với độ lớn của chúng:

\[ \frac{F_1}{F_2} = \frac{d_2}{d_1} \]

2.2. Hợp Lực Song Song Ngược Chiều

Nếu hai lực song song nhưng ngược chiều, hợp lực sẽ có độ lớn bằng hiệu độ lớn của hai lực:

\[ F = |F_1 - F_2| \]

Giá của hợp lực cũng chia khoảng cách giữa hai giá của hai lực theo tỉ lệ nghịch với độ lớn của chúng, tương tự như quy tắc chia trong:

\[ \frac{F_1}{F_2} = \frac{d_2}{d_1} \]

3. Ứng Dụng Trong Thực Tế

Quy tắc hợp lực hai lực song song được ứng dụng rộng rãi trong nhiều lĩnh vực như xây dựng, thiết kế cầu đường, cơ khí, và đặc biệt là trong việc phân tích lực trong các công trình kỹ thuật.

• Đòn bẩy: Một ứng dụng điển hình, trong đó hai lực song song tạo ra mô men xoắn giúp nâng hoặc cân bằng vật thể.
• Cân thăng bằng: Dùng trong thiết kế các loại cân truyền thống, nơi trọng lượng của các vật đối lập được cân bằng qua các lực song song.

4. Bài Tập Thực Hành

Để hiểu rõ hơn về khái niệm này, học sinh thường thực hiện các bài tập liên quan đến tính toán hợp lực, phân tích các lực tác động trên các vật thể đơn giản như thước, đòn bẩy, hoặc cân thăng bằng.

Ví dụ: Xác định lực tác dụng lên vai của hai người khiêng một vật nặng bằng đòn gánh, hoặc tính toán lực tổng hợp từ hai lực song song tác động lên một thanh cứng.

5. Kết Luận

Hiểu rõ và vận dụng đúng quy tắc hợp lực hai lực song song là cơ sở quan trọng trong việc giải quyết các vấn đề liên quan đến lực trong vật lý và kỹ thuật. Nó không chỉ giúp nâng cao khả năng giải bài tập vật lý mà còn ứng dụng hiệu quả trong nhiều lĩnh vực công nghiệp.

Thí nghiệm minh họa về hợp lực hai lực song song giúp học sinh và người học hiểu rõ hơn về khái niệm và quy tắc tổng hợp lực. Dưới đây là một số thí nghiệm đơn giản và dễ thực hiện để minh họa nguyên lý này:

3.1. Thí Nghiệm Với Thước Kẻ và Quả Cân

• Dụng cụ: Một thước kẻ dài, hai quả cân có khối lượng bằng nhau, và một giá đỡ.
• Cách thực hiện: Đặt thước kẻ lên giá đỡ sao cho nó nằm ngang. Treo hai quả cân ở hai đầu của thước kẻ, đảm bảo rằng khoảng cách từ điểm treo đến tâm của thước là bằng nhau. Điều chỉnh vị trí của hai quả cân để thấy rằng khi lực tác dụng là cân bằng (tức là hai lực song song ngược chiều có độ lớn bằng nhau), thước kẻ sẽ nằm yên trong trạng thái cân bằng.
• Kết quả: Thước kẻ nằm yên minh họa cho trường hợp hai lực song song ngược chiều và có độ lớn bằng nhau, tạo thành một hệ lực cân bằng.

3.2. Thí Nghiệm Về Cân Bằng Lực Với Đòn Bẩy

• Dụng cụ: Một thanh đòn bẩy, các quả cân có khối lượng khác nhau, và một điểm tựa.
• Cách thực hiện: Đặt thanh đòn bẩy lên điểm tựa để tạo thành một hệ đòn bẩy. Đặt một quả cân nặng \( F_1 \) ở một bên và hai quả cân nhẹ hơn \( F_2 \) và \( F_3 \) ở bên kia. Điều chỉnh khoảng cách từ các quả cân đến điểm tựa sao cho đòn bẩy nằm ngang.
• Kết quả: Khi đòn bẩy nằm ngang, hệ lực này cho thấy rằng tổng hợp lực từ hai lực nhỏ hơn (song song cùng chiều) có thể cân bằng với một lực lớn hơn ở phía đối diện, minh họa cho quy tắc tổng hợp lực song song.

3.3. Thí Nghiệm Với Hai Lực Song Song Cùng Chiều

• Dụng cụ: Một bàn gỗ, hai lực kế, và một vật nặng.
• Cách thực hiện: Đặt vật nặng trên bàn. Dùng hai lực kế kéo vật nặng theo cùng một phương và cùng một chiều. Ghi nhận lực đo được từ hai lực kế.
• Kết quả: Tổng lực đo được từ hai lực kế sẽ bằng với trọng lượng của vật nặng, minh họa cho trường hợp tổng hợp hai lực song song cùng chiều.

Các thí nghiệm này không chỉ minh họa rõ ràng quy tắc hợp lực hai lực song song mà còn giúp củng cố kiến thức vật lý cơ bản, đồng thời tăng cường khả năng phân tích và giải quyết các vấn đề về lực trong thực tiễn.

Hợp lực của hai lực song song là một nguyên lý cơ bản trong vật lý và được ứng dụng rộng rãi trong nhiều lĩnh vực thực tế, từ xây dựng, cơ khí, cho đến thiết kế và kiến trúc. Dưới đây là một số ứng dụng tiêu biểu:

4.1. Ứng Dụng Trong Xây Dựng

• Cầu và dầm: Trong các công trình cầu và dầm, lực từ các phương tiện hoặc tải trọng được chia đều và tác động song song lên các dầm chịu lực. Các dầm này phải chịu lực song song, và hợp lực này giúp duy trì sự ổn định của công trình.
• Giàn giáo và kết cấu: Khi dựng các giàn giáo hoặc kết cấu nhà ở, các thanh dầm chịu lực song song thường được lắp đặt để đảm bảo tải trọng được phân bố đều và tránh hiện tượng sập đổ.

4.2. Ứng Dụng Trong Cơ Khí

• Thiết kế máy móc: Trong thiết kế máy móc, các bộ phận chịu lực như trục quay, đòn bẩy và bánh răng thường phải chịu các lực song song. Việc tính toán hợp lực giúp đảm bảo rằng các bộ phận này hoạt động hiệu quả mà không bị biến dạng.
• Hệ thống treo ô tô: Lực tác dụng lên hệ thống treo của ô tô, bao gồm các lò xo và giảm xóc, là một ví dụ điển hình của hai lực song song. Các lực này cần được tổng hợp chính xác để đảm bảo sự thoải mái và an toàn khi vận hành xe.

4.3. Ứng Dụng Trong Thiết Kế Và Kiến Trúc

• Thiết kế nội thất: Khi bố trí nội thất như kệ sách hoặc tủ, các lực từ vật nặng trên bề mặt cần được phân bố đều để tránh làm hỏng hoặc gãy kết cấu. Đây là nơi nguyên lý hợp lực hai lực song song được áp dụng để đảm bảo sự ổn định.
• Kiến trúc cầu thang: Trong thiết kế cầu thang, các bậc thang và thanh đỡ phải chịu lực song song từ trọng lượng của người sử dụng. Việc tính toán hợp lực giúp đảm bảo cầu thang đủ bền và an toàn.

Những ứng dụng này cho thấy tầm quan trọng của việc hiểu và áp dụng nguyên lý hợp lực hai lực song song trong thực tiễn, giúp đảm bảo an toàn và hiệu quả trong nhiều lĩnh vực kỹ thuật và đời sống.

Để hiểu rõ hơn về nguyên lý hợp lực hai lực song song, việc thực hành thông qua các bài tập và ví dụ cụ thể là rất cần thiết. Dưới đây là một số bài tập và ví dụ minh họa giúp củng cố kiến thức này:

5.1. Bài Tập Thực Hành

1. Bài tập 1: Hai lực song song cùng chiều có độ lớn lần lượt là \( F_1 = 30 \, \text{N} \) và \( F_2 = 50 \, \text{N} \). Hãy xác định độ lớn của hợp lực, phương, chiều và vị trí của hợp lực.
2. Bài tập 2: Hai lực song song ngược chiều tác dụng lên một thanh ngang có độ lớn lần lượt là \( F_1 = 100 \, \text{N} \) và \( F_2 = 60 \, \text{N} \). Tính hợp lực và xác định vị trí đặt hợp lực.
3. Bài tập 3: Cho hai lực song song cùng chiều tác dụng lên một vật với độ lớn \( F_1 = 40 \, \text{N} \) và \( F_2 = 60 \, \text{N} \). Lực thứ nhất tác dụng tại điểm cách tâm O của vật 2m, lực thứ hai tác dụng tại điểm cách tâm O 3m. Tìm độ lớn và vị trí của hợp lực.

5.2. Ví Dụ Minh Họa

• Ví dụ 1: Hai người cùng đẩy một chiếc xe theo cùng một hướng với lực lần lượt là 40N và 60N. Tổng hợp lực mà chiếc xe nhận được là 100N theo hướng mà cả hai người đang đẩy. Điều này minh họa cho trường hợp hợp lực của hai lực song song cùng chiều.
• Ví dụ 2: Một tấm bảng bị kéo bởi hai lực song song ngược chiều, lực thứ nhất có độ lớn 80N, lực thứ hai có độ lớn 50N. Hợp lực sẽ bằng 30N theo hướng của lực lớn hơn. Đây là một minh họa cụ thể cho việc tổng hợp hai lực song song ngược chiều.

Các bài tập và ví dụ trên không chỉ giúp củng cố kiến thức lý thuyết mà còn phát triển khả năng phân tích và giải quyết vấn đề trong thực tế, từ đó nắm vững nguyên lý hợp lực hai lực song song.

Việc hiểu biết về hợp lực hai lực song song không chỉ có ý nghĩa quan trọng trong việc nắm bắt các khái niệm cơ bản của vật lý, mà còn đóng vai trò then chốt trong nhiều lĩnh vực thực tiễn. Sự am hiểu này giúp người học nắm vững nguyên lý cân bằng lực, từ đó ứng dụng trong thiết kế, xây dựng, và nhiều lĩnh vực kỹ thuật khác.

6.1. Vai trò trong học tập và nghiên cứu

• Cơ sở lý thuyết vững chắc: Nắm vững hợp lực hai lực song song giúp học sinh, sinh viên hiểu rõ hơn về các khái niệm cơ bản trong cơ học, từ đó dễ dàng tiếp thu các kiến thức phức tạp hơn.
• Phát triển tư duy logic: Khi giải các bài toán liên quan đến hợp lực hai lực song song, người học được rèn luyện khả năng tư duy logic và phân tích vấn đề một cách hệ thống.
• Nền tảng cho nghiên cứu khoa học: Hiểu biết sâu về hợp lực là cơ sở để thực hiện các nghiên cứu chuyên sâu trong lĩnh vực vật lý và kỹ thuật.

6.2. Ảnh hưởng đến các lĩnh vực kỹ thuật và khoa học

• Ứng dụng trong xây dựng và thiết kế: Trong xây dựng, việc áp dụng hợp lực hai lực song song giúp đảm bảo tính ổn định và bền vững của các công trình. Các kỹ sư cần hiểu rõ nguyên lý này để thiết kế các kết cấu chịu lực hiệu quả.
• Tối ưu hóa trong sản xuất: Việc hiểu rõ hợp lực hai lực song song giúp các nhà sản xuất tối ưu hóa quy trình, giảm thiểu rủi ro và tăng năng suất lao động.
• Phát triển công nghệ mới: Các nguyên lý của hợp lực hai lực song song được ứng dụng trong việc phát triển các công nghệ mới, đặc biệt trong lĩnh vực robot, cơ điện tử và năng lượng tái tạo.

Nhìn chung, việc hiểu biết về hợp lực hai lực song song không chỉ giúp nắm vững các kiến thức cơ bản trong vật lý mà còn mở ra nhiều cơ hội ứng dụng trong thực tiễn, góp phần vào sự phát triển của khoa học kỹ thuật và công nghệ.