Cách Tính Lực Tương Tác Giữa Hai Điện Tích: Hướng Dẫn Chi Tiết và Bài Tập Minh Họa

Trong vật lý, lực tương tác giữa hai điện tích được tính bằng công thức của Định luật Coulomb. Đây là kiến thức quan trọng trong chương trình vật lý phổ thông, cụ thể là lớp 11. Dưới đây là cách tính và các khái niệm liên quan đến lực tương tác giữa hai điện tích.

1. Định luật Coulomb

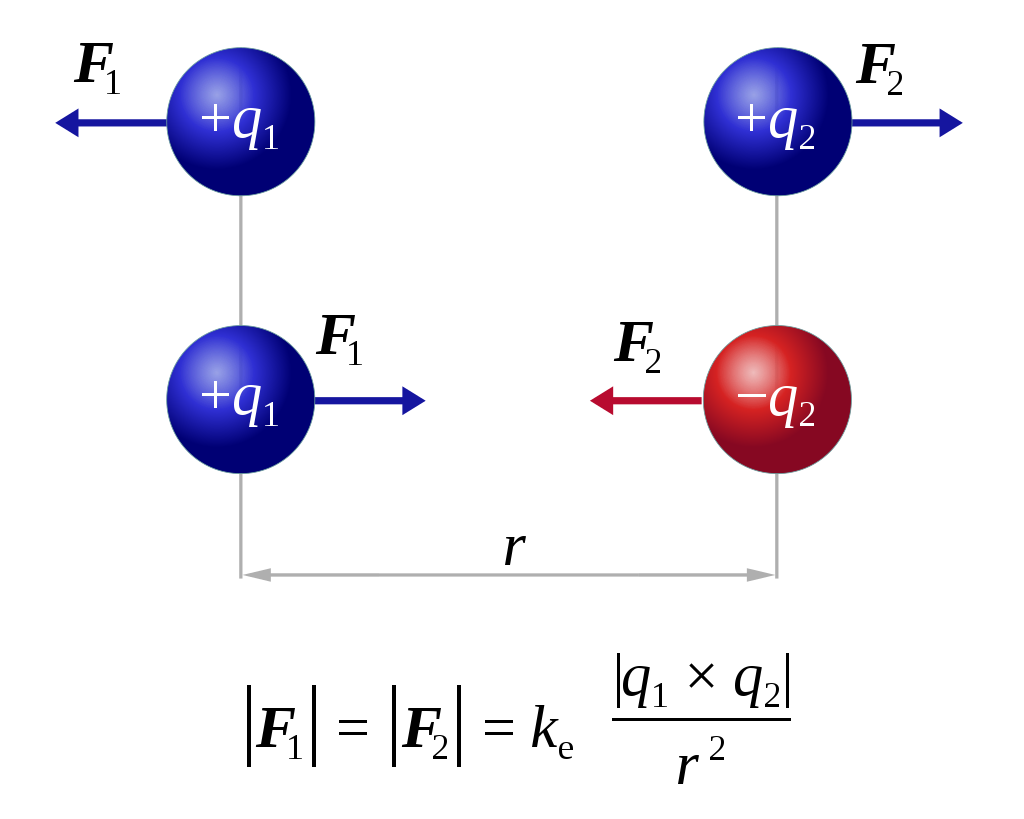
Định luật Coulomb phát biểu rằng lực tương tác tĩnh điện giữa hai điện tích điểm có phương trùng với đường thẳng nối hai điện tích, có độ lớn tỉ lệ thuận với tích độ lớn của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

Công thức tổng quát:

\[
F = k \cdot \frac{|q_1 \cdot q_2|}{r^2}
\]

• F: Lực tương tác giữa hai điện tích (N).
• q₁, q₂: Độ lớn của hai điện tích (C).
• r: Khoảng cách giữa hai điện tích (m).
• k: Hằng số điện môi của môi trường, trong chân không, k = 9 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2.

2. Hằng số điện môi và môi trường

Hằng số điện môi \(\varepsilon\) là đại lượng đặc trưng cho khả năng dẫn điện của môi trường. Trong các môi trường khác nhau, giá trị của \(\varepsilon\) sẽ khác nhau, từ đó làm thay đổi độ lớn của lực tương tác.

3. Ứng dụng của Định luật Coulomb

Định luật Coulomb không chỉ được sử dụng để tính toán lực giữa các điện tích mà còn được ứng dụng rộng rãi trong các lĩnh vực như điện học, hóa học và kỹ thuật điện tử. Nó giúp giải thích các hiện tượng như nhiễm điện do cọ xát, tương tác giữa các điện tích trong các thiết bị điện và nhiều ứng dụng thực tiễn khác.

4. Ví dụ minh họa

Giả sử có hai điện tích điểm \[ q_1 = 10^{-6} \, \text{C} \] và \[ q_2 = 2 \times 10^{-6} \, \text{C} \] đặt cách nhau 5 cm trong chân không. Ta có thể tính lực tương tác giữa chúng như sau:

\[
F = 9 \times 10^9 \cdot \frac{|10^{-6} \cdot 2 \times 10^{-6}|}{(0.05)^2} = 7.2 \, \text{N}
\]

Như vậy, lực tương tác giữa hai điện tích này là 7.2 N.

5. Lưu ý khi tính toán

• Đảm bảo sử dụng đúng đơn vị SI để tránh nhầm lẫn.
• Khoảng cách \(r\) phải được đo chính xác và chuyển đổi sang mét nếu cần thiết.
• Trong các môi trường khác chân không, cần điều chỉnh hằng số điện môi \(\varepsilon\) cho phù hợp.

Đây là những kiến thức cơ bản nhưng rất quan trọng trong việc hiểu về lực tương tác giữa các điện tích và các ứng dụng của nó trong khoa học và kỹ thuật.

Lực tương tác giữa hai điện tích là một khái niệm cơ bản trong vật lý, đặc biệt quan trọng trong lĩnh vực điện học. Khi hai vật mang điện tích đặt gần nhau, chúng sẽ tác động lẫn nhau bằng một lực, được gọi là lực tương tác điện. Lực này có thể là lực hút hoặc lực đẩy, phụ thuộc vào dấu của các điện tích:

• Nếu hai điện tích cùng dấu (cả hai đều dương hoặc âm), chúng sẽ đẩy nhau.
• Nếu hai điện tích trái dấu (một dương, một âm), chúng sẽ hút nhau.

Độ lớn của lực tương tác giữa hai điện tích được xác định bằng Định luật Coulomb, một trong những định luật cơ bản của điện học. Công thức của định luật Coulomb như sau:

\[ F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \]

Trong đó:

• \(F\) là độ lớn của lực tương tác (đơn vị Newton, N)
• \(k\) là hằng số Coulomb, có giá trị khoảng \(8.99 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2\)
• \(q_1\) và \(q_2\) là giá trị của hai điện tích (đơn vị Coulomb, C)
• \(r\) là khoảng cách giữa hai điện tích (đơn vị mét, m)

Lực tương tác giữa hai điện tích không chỉ phụ thuộc vào độ lớn của các điện tích và khoảng cách giữa chúng, mà còn phụ thuộc vào môi trường mà chúng đặt trong đó. Trong môi trường có hằng số điện môi khác nhau, lực tương tác có thể thay đổi, yếu đi hoặc mạnh lên.

Hiểu rõ về lực tương tác giữa hai điện tích là nền tảng để tiếp cận và giải quyết nhiều vấn đề khác trong điện học, từ việc phân tích điện trường đến tính toán các hiện tượng phức tạp trong kỹ thuật điện tử và công nghệ.

Định luật Coulomb là một trong những định luật cơ bản của điện học, được phát hiện bởi nhà vật lý người Pháp Charles-Augustin de Coulomb vào thế kỷ 18. Định luật này mô tả lực tương tác giữa hai điện tích điểm, cho biết lực này phụ thuộc vào độ lớn của các điện tích và khoảng cách giữa chúng.

Theo định luật Coulomb, lực tương tác giữa hai điện tích điểm \(q_1\) và \(q_2\) có độ lớn được xác định bởi công thức:

\[ F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \]

Trong đó:

• \(F\) là độ lớn của lực tương tác (đơn vị Newton, N)
• \(k\) là hằng số Coulomb, giá trị xấp xỉ \(8.99 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2\)
• \(q_1\) và \(q_2\) là giá trị của hai điện tích (đơn vị Coulomb, C)
• \(r\) là khoảng cách giữa hai điện tích (đơn vị mét, m)

Lực tương tác này có đặc điểm:

• Phương của lực tương tác trùng với đường thẳng nối liền hai điện tích điểm.
• Chiều của lực: nếu hai điện tích cùng dấu, lực sẽ đẩy nhau; nếu khác dấu, lực sẽ hút nhau.

Định luật Coulomb không chỉ áp dụng trong chân không mà còn có thể áp dụng trong các môi trường khác, với sự điều chỉnh của hằng số điện môi \(\varepsilon\). Khi đó, công thức tính lực tương tác giữa hai điện tích trở thành:

\[ F = \frac{1}{4\pi \varepsilon} \cdot \frac{|q_1 \cdot q_2|}{r^2} \]

Trong đó:

• \(\varepsilon\) là hằng số điện môi của môi trường, thể hiện khả năng của môi trường trong việc suy giảm lực tương tác điện.

Định luật Coulomb là nền tảng của nhiều hiện tượng và ứng dụng trong điện học, từ việc giải thích các hiện tượng tĩnh điện đến thiết kế các thiết bị điện tử hiện đại.

Để tính lực tương tác giữa hai điện tích điểm, chúng ta sử dụng định luật Coulomb, được phát biểu như sau:

1. Công thức:

   Lực tương tác \( F \) giữa hai điện tích điểm \( q_1 \) và \( q_2 \) trong chân không hoặc không khí được tính bằng công thức:

   \[ F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \]

   Trong đó:

   • \( F \) là lực tương tác giữa hai điện tích (đơn vị: Newton, N).
   • \( k \) là hằng số Coulomb, \( k = 9 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2 \).
   • \( q_1 \), \( q_2 \) là độ lớn của hai điện tích (đơn vị: Coulomb, C).
   • \( r \) là khoảng cách giữa hai điện tích (đơn vị: mét, m).

2. Ý nghĩa của công thức:

   • Lực \( F \) sẽ là lực hút nếu hai điện tích trái dấu (\( q_1 \) và \( q_2 \) có dấu khác nhau).
   • Lực \( F \) sẽ là lực đẩy nếu hai điện tích cùng dấu (\( q_1 \) và \( q_2 \) có cùng dấu).
   • Lực tương tác tỉ lệ thuận với tích của độ lớn hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

3. Lực tương tác trong các môi trường khác nhau:

   Khi hai điện tích được đặt trong một môi trường có hằng số điện môi \( \varepsilon \), công thức tính lực tương tác được điều chỉnh như sau:

   \[ F = k \cdot \frac{|q_1 \cdot q_2|}{\varepsilon \cdot r^2} \]
   • \( \varepsilon \) là hằng số điện môi của môi trường, với \( \varepsilon = 1 \) trong chân không hoặc không khí.
   • Hằng số điện môi \( \varepsilon \) càng lớn, lực tương tác giữa các điện tích càng giảm.

4. Các trường hợp đặc biệt:

   • Khi \( r \) rất nhỏ (hai điện tích rất gần nhau), lực tương tác \( F \) sẽ rất lớn.
   • Khi \( r \) rất lớn (hai điện tích rất xa nhau), lực tương tác \( F \) sẽ rất nhỏ, gần như bằng không.
   • Trong môi trường có hằng số điện môi rất cao (ví dụ như nước), lực tương tác giữa hai điện tích có thể bị giảm đi đáng kể.

Dưới đây là một số bài tập minh họa về cách tính lực tương tác giữa hai điện tích, cùng với phương pháp giải chi tiết. Các bài tập này giúp bạn hiểu rõ hơn về cách áp dụng định luật Coulomb trong các tình huống thực tế.

1. Bài tập 1: Tính lực tương tác giữa hai điện tích điểm trong chân không

   Giả sử hai điện tích điểm có giá trị lần lượt là \( q_1 = 3 \times 10^{-6} \, \text{C} \) và \( q_2 = 4 \times 10^{-6} \, \text{C} \), đặt cách nhau một khoảng \( r = 0,2 \, \text{m} \) trong chân không. Hãy tính lực tương tác giữa hai điện tích này.

   Giải:

   Sử dụng công thức Coulomb:

   \[ F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \]

   Trong đó:

   • \( k = 9 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2 \)
   • \( q_1 = 3 \times 10^{-6} \, \text{C} \)
   • \( q_2 = 4 \times 10^{-6} \, \text{C} \)
   • \( r = 0,2 \, \text{m} \)

   Thay các giá trị vào công thức:

   \[ F = 9 \times 10^9 \cdot \frac{3 \times 10^{-6} \cdot 4 \times 10^{-6}}{(0,2)^2} = 2,7 \, \text{N} \]

   Vậy, lực tương tác giữa hai điện tích là 2,7 N.

2. Bài tập 2: Tính lực tương tác trong môi trường có hằng số điện môi

   Hai điện tích \( q_1 = 2 \times 10^{-7} \, \text{C} \) và \( q_2 = -5 \times 10^{-7} \, \text{C} \) được đặt cách nhau \( r = 0,1 \, \text{m} \) trong nước, với hằng số điện môi \( \varepsilon = 80 \). Hãy tính lực tương tác giữa chúng.

   Giải:

   Sử dụng công thức Coulomb điều chỉnh theo hằng số điện môi:

   \[ F = k \cdot \frac{|q_1 \cdot q_2|}{\varepsilon \cdot r^2} \]
   • \( k = 9 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2 \)
   • \( q_1 = 2 \times 10^{-7} \, \text{C} \)
   • \( q_2 = -5 \times 10^{-7} \, \text{C} \)
   • \( r = 0,1 \, \text{m} \)
   • \( \varepsilon = 80 \)

   Thay các giá trị vào công thức:

   \[ F = 9 \times 10^9 \cdot \frac{2 \times 10^{-7} \cdot 5 \times 10^{-7}}{80 \cdot (0,1)^2} = 1,125 \times 10^{-2} \, \text{N} \]

   Vậy, lực tương tác giữa hai điện tích trong nước là 0,01125 N.

3. Bài tập 3: Tính lực tương tác khi thay đổi khoảng cách giữa hai điện tích

   Hai điện tích \( q_1 = 6 \times 10^{-6} \, \text{C} \) và \( q_2 = 3 \times 10^{-6} \, \text{C} \) đặt cách nhau \( r_1 = 0,3 \, \text{m} \). Sau đó, khoảng cách giữa hai điện tích được tăng lên gấp đôi. Hãy tính lực tương tác mới giữa hai điện tích.

   Giải:

   Lực tương tác ban đầu:

   \[ F_1 = k \cdot \frac{|q_1 \cdot q_2|}{r_1^2} \] \p>Thay các giá trị vào: \[ F_1 = 9 \times 10^9 \cdot \frac{6 \times 10^{-6} \cdot 3 \times 10^{-6}}{(0,3)^2} = 1,8 \, \text{N} \]

   Khi khoảng cách tăng gấp đôi, \( r_2 = 2r_1 = 0,6 \, \text{m} \), lực tương tác mới là:

   \[ F_2 = k \cdot \frac{|q_1 \cdot q_2|}{r_2^2} = 9 \times 10^9 \cdot \frac{6 \times 10^{-6} \cdot 3 \times 10^{-6}}{(0,6)^2} = 0,45 \, \text{N} \]

   Vậy, lực tương tác mới là 0,45 N, giảm đi 4 lần so với ban đầu.

Để củng cố kiến thức về lực tương tác giữa hai điện tích, chúng ta sẽ thực hiện một số bài tập và câu hỏi trắc nghiệm. Những bài tập này sẽ giúp bạn hiểu rõ hơn về cách áp dụng định luật Coulomb cũng như các biến đổi trong môi trường khác nhau.

5.1 Câu hỏi trắc nghiệm về lực tương tác giữa hai điện tích

Hãy thử sức với các câu hỏi trắc nghiệm sau đây để kiểm tra hiểu biết của bạn:

1. Câu 1: Lực tương tác giữa hai điện tích tỉ lệ thuận với yếu tố nào dưới đây?
   • A. Bình phương khoảng cách giữa hai điện tích
   • B. Tổng độ lớn của hai điện tích
   • C. Tích độ lớn của hai điện tích
   • D. Độ lớn của một điện tích
2. Câu 2: Nếu khoảng cách giữa hai điện tích tăng gấp đôi, thì lực tương tác giữa chúng sẽ:
   • A. Tăng gấp đôi
   • B. Giảm đi một nửa
   • C. Giảm đi 4 lần
   • D. Không thay đổi
3. Câu 3: Trong môi trường nào dưới đây, lực tương tác giữa hai điện tích là nhỏ nhất?
   • A. Trong không khí
   • B. Trong nước
   • C. Trong chân không
   • D. Trong dầu

5.2 Tóm tắt và hệ thống hóa kiến thức

Sau khi hoàn thành các bài tập và câu hỏi trắc nghiệm, hãy tóm tắt lại các kiến thức đã học để đảm bảo bạn đã nắm vững:

• Định luật Coulomb: Lực tương tác giữa hai điện tích tỉ lệ thuận với tích độ lớn của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng. Công thức của định luật Coulomb là: \[ F = k \frac{{|q_1 \cdot q_2|}}{{r^2}} \] Trong đó:
  • F: Lực tương tác giữa hai điện tích (đơn vị: Newton, N)
  • k: Hằng số Coulomb, có giá trị \(8.99 \times 10^9 \, N \cdot m^2 / C^2\)
  • q₁, q₂: Độ lớn của hai điện tích (đơn vị: Coulomb, C)
  • r: Khoảng cách giữa hai điện tích (đơn vị: mét, m)
• Ứng dụng của định luật Coulomb: Định luật này được áp dụng rộng rãi trong việc tính toán lực tương tác giữa các điện tích trong các môi trường khác nhau như không khí, nước, và chân không.
• Các yếu tố ảnh hưởng đến lực tương tác: Lực tương tác giữa hai điện tích không chỉ phụ thuộc vào độ lớn và khoảng cách của chúng mà còn bị ảnh hưởng bởi môi trường xung quanh, ví dụ trong môi trường điện môi khác nhau.

Bạn nên thường xuyên ôn tập và luyện tập với các bài tập nâng cao để củng cố kiến thức và chuẩn bị tốt cho các bài kiểm tra.