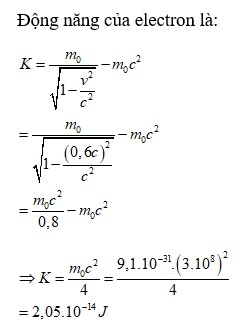Khối lượng nghỉ của electron: Khái niệm, giá trị và ứng dụng trong khoa học hiện đại

Khối lượng nghỉ của electron là một đại lượng vật lý cơ bản, biểu thị khối lượng của electron khi nó không bị ảnh hưởng bởi bất kỳ lực nào và không chuyển động. Đây là một hằng số cơ bản trong vật lý lượng tử và được xác định rất chính xác.

Giá trị của khối lượng nghỉ của electron

Theo các kết quả thí nghiệm và nghiên cứu hiện đại, khối lượng nghỉ của electron được xác định là:

\[
m_e = 9.10938356 \times 10^{-31} \text{ kg}
\]

Tầm quan trọng của khối lượng nghỉ của electron

• Trong vật lý lượng tử: Khối lượng nghỉ của electron là một trong những hằng số cơ bản cần thiết để mô tả các hiện tượng vật lý vi mô, bao gồm các tính toán trong cơ học lượng tử và lý thuyết trường lượng tử.
• Trong hóa học: Khối lượng nghỉ của electron đóng vai trò quan trọng trong việc xác định các tính chất của nguyên tử và phân tử, ảnh hưởng đến các phản ứng hóa học.
• Trong công nghệ: Hiểu biết về khối lượng nghỉ của electron giúp phát triển các công nghệ tiên tiến như vi điện tử và công nghệ bán dẫn.

Các ứng dụng của khối lượng nghỉ của electron

Khối lượng nghỉ của electron có nhiều ứng dụng quan trọng trong khoa học và công nghệ:

1. Phân tích quang phổ: Khối lượng nghỉ của electron giúp trong việc tính toán và dự đoán các vạch quang phổ của nguyên tử.
2. Các thiết bị bán dẫn: Việc phát triển và cải tiến các thiết bị bán dẫn phụ thuộc vào hiểu biết về khối lượng nghỉ của electron.
3. Điện tử học: Các nguyên lý của điện tử học hiện đại dựa trên các đặc tính của electron, bao gồm khối lượng nghỉ của nó.

Kết luận

Khối lượng nghỉ của electron là một đại lượng cơ bản với nhiều ứng dụng quan trọng trong vật lý, hóa học và công nghệ. Việc nghiên cứu và hiểu rõ về đại lượng này giúp chúng ta tiến bộ hơn trong nhiều lĩnh vực khoa học và công nghệ.

Khối lượng nghỉ của electron là khối lượng của electron khi nó ở trạng thái nghỉ, tức là không chuyển động trong hệ quy chiếu quán tính. Đây là một trong những hằng số vật lý cơ bản và quan trọng nhất, thường được ký hiệu là \(m_e\).

Theo lý thuyết tương đối hẹp của Albert Einstein, khối lượng nghỉ của một hạt là khối lượng cố định của hạt đó khi nó không chuyển động, không phụ thuộc vào vận tốc của hạt trong không gian. Đối với electron, khối lượng nghỉ này là một giá trị không đổi, giúp xác định nhiều tính chất quan trọng khác của hạt, chẳng hạn như động năng và năng lượng toàn phần.

Giá trị chính xác của khối lượng nghỉ của electron là:

\[
m_e = 9.10938356 \times 10^{-31} \text{ kg}
\]

Trong hệ đơn vị nguyên tử (atomic units), khối lượng nghỉ của electron được coi là một đơn vị cơ bản, với giá trị:

\[
m_e = 1 \text{ a.u.}
\]

Khối lượng nghỉ của electron không chỉ là một đại lượng quan trọng trong vật lý lý thuyết, mà còn có ý nghĩa thực tiễn trong nhiều lĩnh vực khoa học khác nhau như hóa học, công nghệ vật liệu, và điện tử học. Sự hiểu biết chính xác về khối lượng nghỉ của electron giúp các nhà khoa học và kỹ sư có thể mô phỏng và tính toán các hiện tượng vật lý một cách chính xác hơn.

Khối lượng nghỉ của electron là một đại lượng cơ bản trong vật lý, và nó đã được xác định với độ chính xác cao thông qua nhiều thí nghiệm và phương pháp đo lường khác nhau. Giá trị này đóng vai trò quan trọng trong việc mô tả các tính chất vật lý của electron và các hiện tượng liên quan.

Giá trị chính xác nhất của khối lượng nghỉ của electron được chấp nhận hiện nay là:

\[
m_e = 9.10938356 \times 10^{-31} \text{ kg}
\]

Khối lượng này cũng có thể được biểu diễn dưới nhiều đơn vị khác nhau trong các hệ đơn vị khác nhau:

• Trong hệ CGS: \[m_e = 9.10938356 \times 10^{-28} \text{ g}\]
• Trong hệ đơn vị nguyên tử (a.u.): \[m_e = 1 \text{ a.u.}\]
• Trong đơn vị năng lượng (MeV/\(c^2\)): \[m_e \approx 0.5109989461 \text{ MeV}/c^2\]

Giá trị của khối lượng nghỉ của electron không chỉ là một con số trong các bảng số liệu mà còn là một yếu tố quyết định trong các phép tính về động lực học của hạt, cấu trúc nguyên tử, và các phản ứng hạt nhân. Sự chính xác trong giá trị này giúp các nhà khoa học có thể dự đoán và mô phỏng chính xác các hiện tượng vật lý vi mô.

Khối lượng nghỉ của electron có thể được đo lường thông qua các phương pháp thí nghiệm khác nhau, bao gồm cả phương pháp dựa trên hiệu ứng Zeeman, phương pháp quang phổ học, và các thí nghiệm phân tán electron. Mỗi phương pháp cung cấp những góc nhìn khác nhau, góp phần khẳng định và nâng cao độ chính xác của giá trị này.

Khối lượng nghỉ của electron là một đại lượng vật lý cơ bản, có ảnh hưởng sâu rộng đến nhiều lĩnh vực khoa học và công nghệ. Sự hiểu biết và sử dụng chính xác giá trị này đã mở ra nhiều ứng dụng quan trọng, từ nghiên cứu cơ bản đến phát triển các công nghệ tiên tiến.

3.1 Trong vật lý lượng tử và hạt nhân

Trong vật lý lượng tử, khối lượng nghỉ của electron là yếu tố then chốt để tính toán động năng, thế năng, và các mức năng lượng trong nguyên tử. Ví dụ, trong mô hình Bohr của nguyên tử, khối lượng nghỉ của electron giúp xác định các quỹ đạo của electron xung quanh hạt nhân. Trong vật lý hạt nhân, giá trị này còn được sử dụng để tính toán các phản ứng hạt nhân và phân rã phóng xạ.

3.2 Trong công nghệ bán dẫn

Các thiết bị bán dẫn như diode, transistor, và vi mạch tích hợp dựa vào đặc tính điện tử của các vật liệu bán dẫn, trong đó khối lượng nghỉ của electron đóng vai trò quan trọng trong việc xác định các đặc tính điện của các thiết bị này. Sự di chuyển của các electron trong chất bán dẫn phụ thuộc vào khối lượng nghỉ của chúng, ảnh hưởng đến hiệu suất và tốc độ của các thiết bị điện tử.

3.3 Trong quang phổ học và hóa học

Khối lượng nghỉ của electron là cơ sở cho việc xác định các mức năng lượng và các vạch quang phổ của nguyên tử. Điều này có ứng dụng trong việc phân tích thành phần hóa học của các vật thể xa xôi trong thiên văn học, cũng như trong việc nghiên cứu các phản ứng hóa học ở mức độ nguyên tử và phân tử.

3.4 Trong nghiên cứu và phát triển công nghệ hạt nhân

Khối lượng nghỉ của electron được sử dụng trong việc tính toán động lực học của các hạt trong các phản ứng hạt nhân và quá trình phân hạch, nhiệt hạch. Việc hiểu rõ khối lượng nghỉ của electron giúp tối ưu hóa các lò phản ứng hạt nhân và phát triển các công nghệ năng lượng sạch hơn.

Nhìn chung, khối lượng nghỉ của electron là một đại lượng có ý nghĩa rộng lớn, không chỉ trong việc nghiên cứu lý thuyết mà còn trong các ứng dụng thực tiễn. Sự hiểu biết chính xác về khối lượng nghỉ của electron tiếp tục thúc đẩy sự tiến bộ của khoa học và công nghệ hiện đại.

Khối lượng nghỉ của electron là một đại lượng quan trọng trong việc giải thích và dự đoán các hiện tượng vật lý, đặc biệt là trong các lĩnh vực vật lý lượng tử, thuyết tương đối, và điện động lực học lượng tử. Dưới đây là một số hiện tượng vật lý mà khối lượng nghỉ của electron đóng vai trò then chốt.

4.1 Hiệu ứng quang điện

Hiệu ứng quang điện là hiện tượng khi ánh sáng chiếu vào một vật liệu, các electron bị bức xạ và phát ra khỏi bề mặt vật liệu. Khối lượng nghỉ của electron ảnh hưởng trực tiếp đến động năng của các electron phát ra, xác định thông qua công thức:

\[
E_k = h\nu - \phi
\]

Trong đó, \(E_k\) là động năng của electron, \(h\) là hằng số Planck, \(\nu\) là tần số của ánh sáng, và \(\phi\) là công thoát của vật liệu. Giá trị của khối lượng nghỉ của electron quyết định cách tính toán động năng \(E_k\) và do đó là một yếu tố quyết định trong việc nghiên cứu hiệu ứng quang điện.

4.2 Hiệu ứng Compton

Hiệu ứng Compton mô tả sự tán xạ của photon khi va chạm với electron. Trong quá trình này, photon mất năng lượng và bị tán xạ với góc khác, trong khi electron nhận năng lượng và di chuyển với động năng mới. Công thức Compton mô tả mối quan hệ giữa góc tán xạ và sự thay đổi bước sóng của photon:

\[
\Delta \lambda = \frac{h}{m_e c}(1 - \cos \theta)
\]

Ở đây, \(\Delta \lambda\) là sự thay đổi bước sóng của photon, \(m_e\) là khối lượng nghỉ của electron, \(c\) là vận tốc ánh sáng, và \(\theta\) là góc tán xạ. Khối lượng nghỉ của electron, do đó, là yếu tố quan trọng để xác định sự thay đổi năng lượng của photon trong hiệu ứng Compton.

4.3 Thuyết tương đối hẹp

Trong thuyết tương đối hẹp của Albert Einstein, khối lượng nghỉ của electron liên quan trực tiếp đến năng lượng toàn phần của nó theo công thức:

\[
E = mc^2
\]

Ở đây, \(E\) là năng lượng toàn phần của electron, \(m\) là khối lượng nghỉ của electron, và \(c\) là tốc độ ánh sáng. Công thức này cho thấy mối liên hệ giữa khối lượng và năng lượng, và giải thích cách năng lượng của electron có thể chuyển đổi thành khối lượng và ngược lại, đặc biệt là trong các phản ứng hạt nhân và các hiện tượng liên quan đến năng lượng cao.

4.4 Động lực học lượng tử

Trong cơ học lượng tử, khối lượng nghỉ của electron đóng vai trò quan trọng trong việc xác định động năng của electron trong các hạt nhân nguyên tử. Phương trình Schrödinger, một phương trình cơ bản trong cơ học lượng tử, sử dụng khối lượng nghỉ của electron để tính toán các trạng thái năng lượng của electron trong nguyên tử:

\[
-\frac{\hbar^2}{2m_e} \nabla^2 \psi + V\psi = E\psi
\]

Ở đây, \(\hbar\) là hằng số Planck, \(m_e\) là khối lượng nghỉ của electron, \(\nabla^2\) là toán tử Laplace, \(V\) là thế năng, \(\psi\) là hàm sóng, và \(E\) là năng lượng. Sự hiểu biết chính xác về khối lượng nghỉ của electron là cần thiết để giải các phương trình lượng tử và dự đoán hành vi của các hạt vi mô.

Tóm lại, khối lượng nghỉ của electron là một hằng số quan trọng trong việc hiểu và mô tả các hiện tượng vật lý từ vi mô đến vĩ mô, từ các phản ứng hạt nhân đến các ứng dụng công nghệ hiện đại.

Khối lượng nghỉ của electron (\(m_e\)) là một hằng số vật lý quan trọng và liên kết chặt chẽ với nhiều hằng số vật lý cơ bản khác. Những hằng số này không chỉ định nghĩa tính chất của electron mà còn giúp chúng ta hiểu sâu hơn về các hiện tượng vật lý trong vũ trụ.

5.1 Hằng số Planck (\(h\))

Hằng số Planck là một hằng số cơ bản trong cơ học lượng tử, được sử dụng để mô tả mức độ lượng tử hóa của năng lượng. Nó liên quan trực tiếp đến khối lượng nghỉ của electron trong các phương trình về động năng và các hiện tượng như hiệu ứng quang điện:

\[
E = h\nu - \phi
\]

Ở đây, \(E\) là động năng của electron, \(h\) là hằng số Planck, \(\nu\) là tần số của ánh sáng, và \(\phi\) là công thoát. Khối lượng nghỉ của electron ảnh hưởng đến cách tính toán động năng, đồng thời được liên hệ chặt chẽ với hằng số Planck trong các mô hình vật lý lượng tử.

5.2 Hằng số Coulomb (\(k_e\))

Hằng số Coulomb xác định độ lớn của lực tương tác giữa hai điện tích trong không gian, và nó đóng vai trò quan trọng trong việc tính toán lực tĩnh điện giữa các electron và các hạt nhân. Công thức Coulomb cho lực giữa hai điện tích \(q_1\) và \(q_2\) ở khoảng cách \(r\) là:

\[
F = k_e \frac{|q_1q_2|}{r^2}
\]

Khối lượng nghỉ của electron không trực tiếp xuất hiện trong công thức này, nhưng nó ảnh hưởng đến các tính toán liên quan đến chuyển động của electron xung quanh hạt nhân, cũng như các đặc trưng của cấu trúc nguyên tử.

5.3 Hằng số Rydberg (\(R_\infty\))

Hằng số Rydberg được sử dụng để mô tả các vạch quang phổ của hydro và các nguyên tử tương tự, liên quan đến năng lượng ion hóa và khối lượng của electron:

\[
R_\infty = \frac{m_e e^4}{8 \epsilon_0^2 h^3 c}
\]

Ở đây, \(e\) là điện tích của electron, \(\epsilon_0\) là hằng số điện môi, \(h\) là hằng số Planck, và \(c\) là vận tốc ánh sáng. Khối lượng nghỉ của electron \(m_e\) là một phần không thể thiếu trong việc xác định giá trị của hằng số Rydberg, qua đó ảnh hưởng đến việc tính toán các mức năng lượng trong nguyên tử.

5.4 Tốc độ ánh sáng trong chân không (\(c\))

Tốc độ ánh sáng là một hằng số vật lý cơ bản, liên quan chặt chẽ đến khối lượng nghỉ của electron thông qua công thức nổi tiếng của Einstein:

\[
E = m_e c^2
\]

Công thức này cho thấy mối quan hệ giữa khối lượng nghỉ của electron và năng lượng toàn phần của nó. Tốc độ ánh sáng cũng ảnh hưởng đến các tính toán liên quan đến khối lượng và năng lượng trong các phản ứng hạt nhân và các hiện tượng năng lượng cao.

5.5 Hằng số Dirac (\(\hbar\))

Hằng số Dirac là hằng số Planck chia cho \(2\pi\), và nó được sử dụng rộng rãi trong cơ học lượng tử. Khối lượng nghỉ của electron liên quan đến hằng số này trong các phương trình sóng lượng tử, như phương trình Schrödinger:

\[
-\frac{\hbar^2}{2m_e} \nabla^2 \psi + V\psi = E\psi
\]

Trong đó, \(\hbar\) là hằng số Dirac, \(m_e\) là khối lượng nghỉ của electron, \(\nabla^2\) là toán tử Laplace, \(V\) là thế năng, và \(\psi\) là hàm sóng. Mối liên hệ này cho thấy tầm quan trọng của khối lượng nghỉ của electron trong việc giải các phương trình lượng tử để dự đoán hành vi của các hạt.

Tóm lại, khối lượng nghỉ của electron là một hằng số quan trọng, có liên kết mật thiết với nhiều hằng số vật lý khác. Sự hiểu biết sâu rộng về các mối quan hệ này giúp mở ra nhiều ứng dụng và khám phá mới trong khoa học và công nghệ.

Khối lượng nghỉ của electron là một trong những hằng số vật lý cơ bản và đóng vai trò quan trọng trong việc hiểu biết về cấu trúc và các tương tác vi mô của vật chất. Giá trị chính xác của khối lượng nghỉ của electron, được xác định là 9,10938356 × 10⁻³¹ kg, là nền tảng cho nhiều tính toán và lý thuyết trong vật lý hạt nhân, hóa học, và công nghệ hiện đại.

6.1 Tầm quan trọng của khối lượng nghỉ của electron trong khoa học

Khối lượng nghỉ của electron không chỉ là một tham số trong các phương trình vật lý mà còn là yếu tố then chốt để xác định các đặc tính cơ bản của vật chất. Nó ảnh hưởng trực tiếp đến hành vi của các hạt trong các hiện tượng lượng tử và thuyết tương đối hẹp. Các khám phá và ứng dụng dựa trên khối lượng nghỉ của electron đã giúp đẩy mạnh sự tiến bộ của khoa học vật liệu, công nghệ nano, và điện tử học.

6.2 Những thách thức và hướng nghiên cứu tương lai

Mặc dù giá trị của khối lượng nghỉ của electron đã được xác định với độ chính xác cao, nhưng các nhà khoa học vẫn đang tiếp tục nghiên cứu để hiểu rõ hơn về bản chất của các hạt cơ bản và các lực tương tác giữa chúng. Những thách thức trong việc hợp nhất các lý thuyết vật lý hiện tại như thuyết lượng tử và thuyết tương đối tổng quát là những hướng nghiên cứu đầy tiềm năng, nhằm tìm ra một lý thuyết thống nhất giải thích được tất cả các hiện tượng trong tự nhiên, trong đó khối lượng nghỉ của electron sẽ vẫn là một hằng số quan trọng.