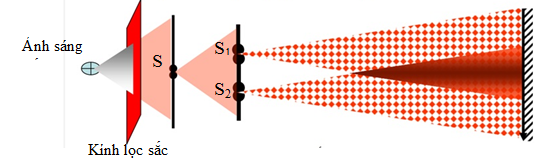
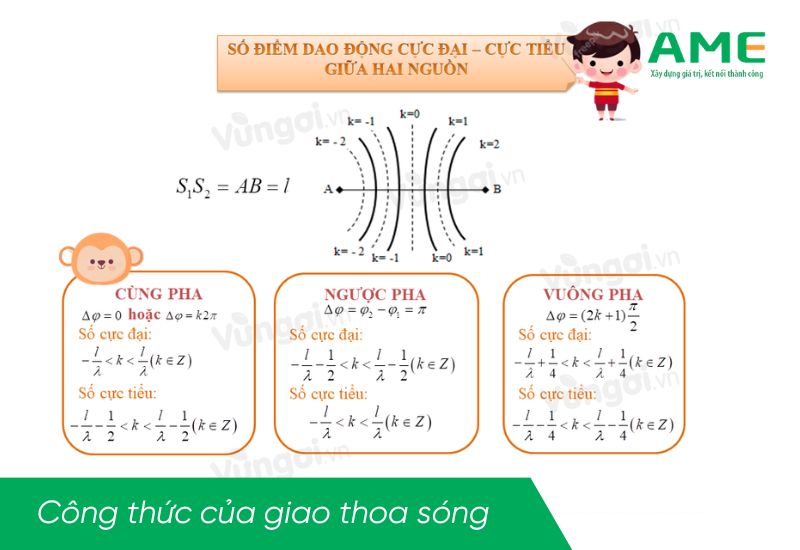
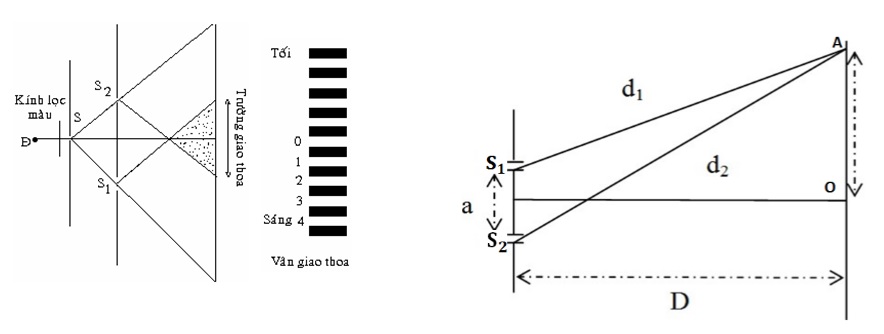
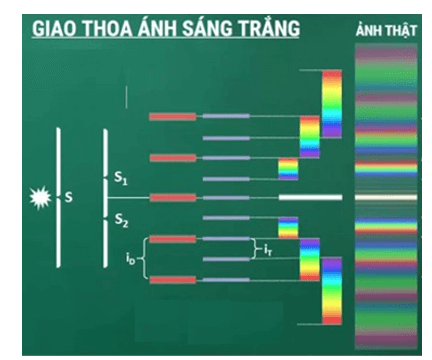
Chủ đề giao thoa sóng vdc: Giao thoa sóng VDC là một trong những hiện tượng vật lý quan trọng và thú vị trong môn Vật lý lớp 12. Bài viết này sẽ giúp bạn hiểu rõ về khái niệm, ứng dụng, và cách giải bài tập liên quan đến giao thoa sóng VDC, từ đó nâng cao kiến thức và kỹ năng học tập của bạn.
Mục lục
Thông Tin Tổng Hợp Về Giao Thoa Sóng VDC
Giao thoa sóng là một hiện tượng vật lý trong đó hai hoặc nhiều sóng gặp nhau và tạo ra một mô hình sóng mới. Trong trường hợp của giao thoa sóng VDC, chủ đề này thường liên quan đến các bài tập và lý thuyết trong chương trình học vật lý lớp 12, đặc biệt là khi chuẩn bị cho các kỳ thi như kỳ thi tốt nghiệp THPT Quốc gia.
1. Khái Niệm Về Giao Thoa Sóng
Giao thoa sóng xảy ra khi hai sóng cùng tần số và biên độ gặp nhau, dẫn đến sự tổng hợp của các sóng tại các điểm khác nhau, tạo ra các điểm giao thoa cực đại và cực tiểu. Mô hình sóng mới này có thể được mô tả bằng phương trình toán học.
Phương trình giao thoa sóng có dạng:
\[
y(x,t) = 2A\cos(kx - \omega t + \phi)
\]
Trong đó:
- \(A\) là biên độ sóng
- \(k\) là số sóng
- \(\omega\) là tần số góc
- \(\phi\) là pha ban đầu
2. Các Dạng Bài Tập Liên Quan
Các bài tập về giao thoa sóng thường được phân loại thành nhiều dạng, bao gồm:
- Dạng 1: Viết phương trình giao thoa sóng, tìm biên độ sóng tại một điểm.
- Dạng 2: Xác định số điểm dao động với biên độ cực đại, cực tiểu.
- Dạng 3: Xác định vị trí, số điểm dao động cùng pha, ngược pha với nguồn sóng.
3. Ứng Dụng Thực Tiễn
Hiện tượng giao thoa sóng có nhiều ứng dụng trong thực tiễn, chẳng hạn như trong công nghệ truyền thông, thiết kế hệ thống loa âm thanh, và các nghiên cứu về sóng âm và sóng ánh sáng.
4. Tài Liệu Tham Khảo
Để học và ôn luyện về giao thoa sóng, học sinh có thể tham khảo các tài liệu ôn thi, sách giáo khoa, và các bài giảng online. Những nguồn tài liệu này cung cấp các phương pháp giải toán tối ưu và bài tập luyện tập giúp nắm vững kiến thức.
5. Kết Luận
Giao thoa sóng là một chủ đề quan trọng trong vật lý, đặc biệt trong giáo dục phổ thông tại Việt Nam. Việc nắm vững kiến thức này không chỉ giúp học sinh đạt kết quả cao trong các kỳ thi mà còn hiểu rõ hơn về các hiện tượng tự nhiên xung quanh.

.png)
1. Giới Thiệu Về Giao Thoa Sóng
Giao thoa sóng là một hiện tượng quan trọng trong vật lý, đặc biệt trong lĩnh vực sóng cơ học. Giao thoa sóng xảy ra khi hai hay nhiều sóng gặp nhau tại một điểm trong không gian, dẫn đến sự kết hợp của chúng để tạo ra một mô hình sóng mới.
Trong giao thoa sóng, các sóng có thể cộng hưởng hoặc triệt tiêu lẫn nhau tùy thuộc vào pha của chúng. Các điểm mà hai sóng gặp nhau và tăng cường lẫn nhau được gọi là cực đại giao thoa, còn các điểm mà hai sóng triệt tiêu lẫn nhau được gọi là cực tiểu giao thoa.
Phương trình của một sóng đơn giản có thể được biểu diễn dưới dạng:
\[
y(x,t) = A \cos(kx - \omega t + \phi)
\]
Trong đó:
- \(A\) là biên độ sóng
- \(k\) là số sóng
- \(\omega\) là tần số góc
- \(\phi\) là pha ban đầu
Khi hai sóng có cùng tần số và biên độ gặp nhau, phương trình sóng tổng hợp sẽ là:
\[
y_{\text{tổng hợp}} = 2A \cos\left(\frac{\Delta \phi}{2}\right) \cos(kx - \omega t + \phi_{\text{tb}})
\]
Trong đó:
- \(\Delta \phi\) là độ lệch pha giữa hai sóng
- \(\phi_{\text{tb}}\) là pha trung bình của hai sóng
Giao thoa sóng có nhiều ứng dụng trong thực tiễn như trong công nghệ truyền thông, kỹ thuật đo đạc, và nghiên cứu khoa học. Hiểu rõ về giao thoa sóng giúp chúng ta khám phá sâu hơn về bản chất của sóng và những hiện tượng liên quan.
2. Phân Loại Và Phương Pháp Giải Bài Tập Giao Thoa Sóng
Giao thoa sóng là một chủ đề quan trọng trong vật lý, đặc biệt là trong các kỳ thi THPT Quốc gia. Bài toán giao thoa sóng có thể được phân loại thành nhiều dạng khác nhau, mỗi dạng yêu cầu các phương pháp giải riêng biệt. Dưới đây là các phân loại chính và phương pháp giải cho từng loại bài tập giao thoa sóng.
2.1. Phân Loại Bài Tập Giao Thoa Sóng
- Dạng 1: Bài toán viết phương trình giao thoa sóng.
- Dạng 2: Bài toán xác định vị trí các điểm dao động cực đại, cực tiểu.
- Dạng 3: Bài toán tìm số điểm dao động cùng pha, ngược pha.
- Dạng 4: Bài toán về đồ thị giao thoa sóng trên dây.
2.2. Phương Pháp Giải Bài Tập Giao Thoa Sóng
Mỗi dạng bài tập giao thoa sóng có phương pháp giải riêng, bao gồm việc thiết lập phương trình sóng và sử dụng các công thức cơ bản để tìm kiếm các giá trị cần thiết.
2.2.1. Viết Phương Trình Giao Thoa Sóng
Để viết phương trình giao thoa của hai sóng, chúng ta cần bắt đầu từ phương trình sóng cơ bản:
\[
y_1(x,t) = A \cos(kx - \omega t)
\]
\[
y_2(x,t) = A \cos(kx - \omega t + \Delta \phi)
\]
\]
Phương trình giao thoa tổng hợp sẽ là:
\[
y(x,t) = y_1(x,t) + y_2(x,t) = 2A \cos\left(\frac{\Delta \phi}{2}\right) \cos(kx - \omega t + \frac{\Delta \phi}{2})
\]
2.2.2. Xác Định Vị Trí Cực Đại, Cực Tiểu
Vị trí cực đại (điểm dao động mạnh nhất) xảy ra khi điều kiện sau được thỏa mãn:
\[
\Delta \phi = 2k\pi, \quad k \in \mathbb{Z}
\]
Vị trí cực tiểu (điểm dao động yếu nhất) xảy ra khi:
\[
\Delta \phi = (2k+1)\pi, \quad k \in \mathbb{Z}
\]
2.2.3. Xác Định Số Điểm Dao Động Cùng Pha, Ngược Pha
Điểm dao động cùng pha khi pha của hai sóng bằng nhau, và điểm dao động ngược pha khi pha của hai sóng chênh lệch \( \pi \).
2.2.4. Giải Bài Toán Đồ Thị Giao Thoa Sóng
Phân tích đồ thị giúp xác định biên độ, tần số, và vị trí các điểm dao động cực đại và cực tiểu trên một sợi dây hoặc trong một môi trường sóng.

3. Tài Liệu Ôn Tập Và Bài Giảng Liên Quan Đến Giao Thoa Sóng
Để nắm vững kiến thức về giao thoa sóng, học sinh cần có một bộ tài liệu ôn tập và các bài giảng đầy đủ, chi tiết. Dưới đây là các nguồn tài liệu và bài giảng phổ biến giúp học sinh củng cố kiến thức và chuẩn bị tốt cho các kỳ thi.
3.1. Sách Giáo Khoa Và Tài Liệu Ôn Tập
- Sách giáo khoa Vật lý 12: Đây là tài liệu cơ bản và quan trọng nhất, cung cấp lý thuyết và các bài tập mẫu về giao thoa sóng.
- Tài liệu ôn tập chuyên đề giao thoa sóng: Các sách tham khảo như "Chinh phục kỳ thi THPT Quốc gia" thường có các chương chuyên đề về sóng cơ học và giao thoa sóng.
- Sách bài tập nâng cao: Để luyện tập thêm, học sinh có thể sử dụng các sách bài tập nâng cao nhằm thực hành nhiều dạng bài khác nhau.
3.2. Bài Giảng Trực Tuyến Và Video Hướng Dẫn
- Video bài giảng trên Youtube: Nhiều giáo viên uy tín có các video bài giảng chi tiết về giao thoa sóng, phân tích từ cơ bản đến nâng cao.
- Khóa học online: Các nền tảng học tập trực tuyến như Hocmai, Tuyensinh247 cung cấp các khóa học chi tiết về vật lý, bao gồm chuyên đề giao thoa sóng.
- Bài giảng livestream: Một số giáo viên thường xuyên livestream trên các mạng xã hội, giải đáp các thắc mắc về giao thoa sóng và các chủ đề liên quan.
3.3. Đề Thi Thử Và Bài Tập Luyện Tập
- Đề thi thử THPT Quốc gia: Các đề thi thử từ các trường chuyên hoặc các trung tâm luyện thi giúp học sinh làm quen với cấu trúc đề thi và luyện kỹ năng làm bài.
- Bộ đề trắc nghiệm trực tuyến: Các trang web như Vndoc, Violet cung cấp các bộ đề trắc nghiệm giao thoa sóng giúp học sinh tự luyện tập và đánh giá trình độ.
- Diễn đàn học tập: Học sinh có thể tham gia các diễn đàn học tập để trao đổi kinh nghiệm, chia sẻ tài liệu và hỏi đáp về giao thoa sóng.
Với những tài liệu và bài giảng này, học sinh có thể tự tin hơn trong việc nắm vững kiến thức và đạt kết quả cao trong các kỳ thi liên quan đến giao thoa sóng.

XEM THÊM:
4. Các Dạng Bài Tập Mở Rộng Về Giao Thoa Sóng
Các bài tập mở rộng về giao thoa sóng không chỉ giúp học sinh nắm vững lý thuyết mà còn phát triển kỹ năng tư duy phân tích và giải quyết vấn đề. Dưới đây là một số dạng bài tập mở rộng thường gặp và phương pháp giải chi tiết cho từng dạng.
4.1. Bài Tập Xác Định Tần Số Và Bước Sóng
Trong các bài toán này, yêu cầu xác định tần số \(f\) và bước sóng \(\lambda\) của sóng từ các dữ liệu liên quan đến giao thoa sóng.
- Cho hai nguồn sóng cùng tần số, bài toán yêu cầu tính bước sóng dựa trên khoảng cách giữa các cực đại liên tiếp:
\[
\lambda = \frac{d}{k}
\]
Trong đó, \(d\) là khoảng cách giữa hai cực đại gần nhất, \(k\) là số nguyên.
4.2. Bài Tập Xác Định Vị Trí Giao Thoa
Bài toán yêu cầu xác định vị trí các điểm cực đại và cực tiểu trên một đoạn thẳng hoặc trong một vùng không gian cụ thể.
- Để tìm vị trí các điểm cực đại (vị trí dao động mạnh nhất):
\[
d_1 - d_2 = k\lambda
\]
Trong đó, \(d_1\) và \(d_2\) là khoảng cách từ điểm cần tìm đến hai nguồn sóng, \(k\) là số nguyên.
4.3. Bài Tập Về Pha Của Sóng
Bài toán yêu cầu tính toán hoặc so sánh pha của sóng tại các điểm khác nhau trong vùng giao thoa.
- Điều kiện để hai sóng có cùng pha tại một điểm:
- Điều kiện để hai sóng có pha lệch nhau \(180^\circ\) (ngược pha):
\[
\Delta \phi = 2k\pi
\]
\[
\Delta \phi = (2k+1)\pi
\]
4.4. Bài Tập Đồ Thị Giao Thoa
Bài tập yêu cầu phân tích và vẽ đồ thị của sóng giao thoa, xác định biên độ, tần số và vị trí các điểm cực đại, cực tiểu.
- Vẽ đồ thị mô tả sự thay đổi biên độ của sóng theo thời gian và không gian.
- Xác định các vị trí mà biên độ sóng bằng 0 hoặc cực đại dựa trên đồ thị.
Các dạng bài tập trên giúp học sinh phát triển tư duy logic và kỹ năng giải quyết vấn đề, từ đó củng cố kiến thức về giao thoa sóng.

5. Kết Luận Và Đánh Giá Chung
Giao thoa sóng là một hiện tượng quan trọng trong vật lý, không chỉ mang lại sự hiểu biết sâu sắc về tính chất của sóng mà còn đóng vai trò quan trọng trong nhiều ứng dụng thực tế. Qua các phần đã trình bày, ta có thể thấy rằng việc hiểu và áp dụng các khái niệm về giao thoa sóng không chỉ giúp học sinh nắm vững kiến thức cơ bản mà còn phát triển khả năng tư duy phân tích và giải quyết vấn đề.
Những bài tập mở rộng và tài liệu ôn tập đa dạng đã được đề cập giúp học sinh củng cố kiến thức và chuẩn bị kỹ càng cho các kỳ thi. Từ việc xác định vị trí các điểm dao động đến việc phân tích đồ thị, mỗi dạng bài tập đều góp phần nâng cao kỹ năng và sự tự tin của học sinh trong việc đối mặt với các bài toán phức tạp.
Nhìn chung, giao thoa sóng không chỉ là một chủ đề học thuật mà còn mở ra nhiều cánh cửa để khám phá các hiện tượng vật lý thú vị trong cuộc sống. Sự kiên trì và chăm chỉ trong việc học tập và luyện tập sẽ giúp học sinh đạt được những thành tựu đáng kể trong lĩnh vực này.
Cuối cùng, giao thoa sóng là một lĩnh vực đáng để nghiên cứu và học tập, bởi nó không chỉ giúp chúng ta hiểu rõ hơn về thế giới tự nhiên mà còn đóng góp vào nhiều ứng dụng công nghệ hiện đại.