Chủ đề công thức tính điện trở phụ thuộc nhiệt độ: Công thức tính điện trở phụ thuộc nhiệt độ là kiến thức quan trọng trong lĩnh vực điện tử và vật lý. Bài viết này sẽ giúp bạn hiểu rõ về cách thức hoạt động, công thức tính toán cụ thể, và các ứng dụng thực tiễn trong công nghiệp, từ đó tối ưu hóa hiệu suất của các thiết bị điện.
Mục lục
- Công thức tính điện trở phụ thuộc nhiệt độ
- 1. Khái niệm về điện trở và sự phụ thuộc vào nhiệt độ
- 2. Công thức tính điện trở phụ thuộc nhiệt độ cơ bản
- 3. Công thức nâng cao cho các vật liệu đặc biệt
- 4. Ứng dụng của công thức tính điện trở phụ thuộc nhiệt độ trong công nghiệp
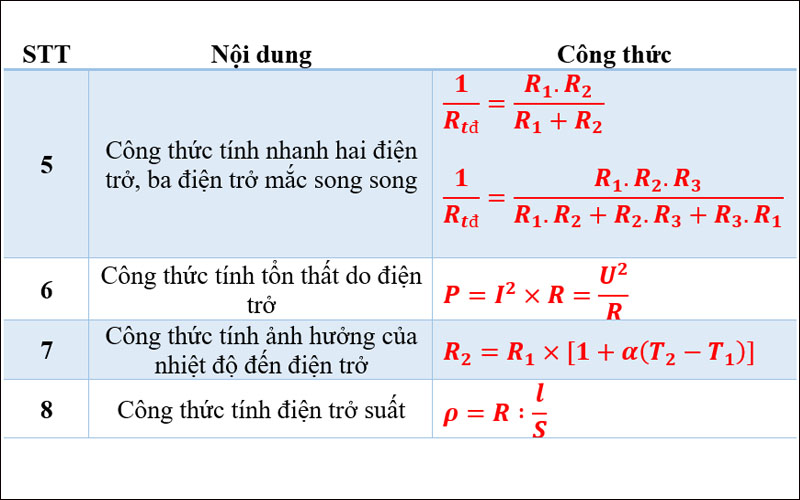
- 5. So sánh các phương pháp tính điện trở theo nhiệt độ
Công thức tính điện trở phụ thuộc nhiệt độ
Trong lĩnh vực vật lý và kỹ thuật điện, điện trở của một vật liệu kim loại thường thay đổi khi nhiệt độ thay đổi. Sự phụ thuộc này có thể được mô tả bởi các công thức toán học cụ thể, dựa trên các đặc tính của vật liệu.
Công thức cơ bản
Điện trở \( R \) của một dây kim loại phụ thuộc vào nhiệt độ \( t \) có thể được tính bằng công thức:
\[
R = R_0 \left[ 1 + \alpha (t - t_0) \right]
\]
- \( R \) là điện trở của vật liệu tại nhiệt độ \( t \) (đơn vị: Ohm).
- \( R_0 \) là điện trở của vật liệu tại nhiệt độ chuẩn \( t_0 \), thường là 20°C hoặc 25°C (đơn vị: Ohm).
- \( \alpha \) là hệ số nhiệt điện trở, biểu thị mức độ thay đổi điện trở theo nhiệt độ (đơn vị: 1/°C).
- \( t \) là nhiệt độ cần tính điện trở (đơn vị: °C).
- \( t_0 \) là nhiệt độ chuẩn, thường là 0°C, 20°C, hoặc 25°C (đơn vị: °C).
Công thức nâng cao
Đối với một số vật liệu đặc biệt như Platin trong cảm biến nhiệt độ RTD, công thức tính điện trở phụ thuộc vào nhiệt độ có thể phức tạp hơn, chẳng hạn:
\[
R_t = R_0 \left( 1 + AT + BT^2 + C(T-100)T^3 \right)
\]
- \( R_t \) là điện trở tại nhiệt độ \( T \) (đơn vị: Ohm).
- \( R_0 \) là điện trở tại nhiệt độ chuẩn (0°C) (đơn vị: Ohm).
- \( A, B, C \) là các hằng số phụ thuộc vào vật liệu cụ thể (đơn vị: 1/°C, 1/°C², 1/°C³).
- \( T \) là nhiệt độ hiện tại (đơn vị: °C).
Ứng dụng thực tiễn
Công thức này được ứng dụng rộng rãi trong nhiều lĩnh vực như:
- Thiết kế mạch điện tử.
- Sản xuất các loại cảm biến nhiệt độ như RTD, PT100, và các thiết bị đo nhiệt độ khác.
- Tính toán và dự đoán sự thay đổi điện trở trong các hệ thống chịu ảnh hưởng nhiệt độ cao, như động cơ điện và thiết bị điện tử công suất.
Bảng tra cứu điện trở theo nhiệt độ
Bảng tra cứu dưới đây giúp dễ dàng tìm giá trị điện trở của một số loại vật liệu ở các mức nhiệt độ khác nhau:
| Nhiệt độ (°C) | Điện trở của PT100 (Ohm) |
|---|---|
| 0 | 100.00 |
| 100 | 138.50 |
| 200 | 175.86 |
| 300 | 212.05 |

.png)
1. Khái niệm về điện trở và sự phụ thuộc vào nhiệt độ
Điện trở là một đại lượng vật lý biểu thị khả năng cản trở dòng điện của một vật liệu. Điện trở được ký hiệu là \(R\) và đơn vị đo là Ohm (Ω). Nó thể hiện mức độ khó khăn mà dòng điện gặp phải khi di chuyển qua vật liệu.
Sự phụ thuộc của điện trở vào nhiệt độ là một hiện tượng quan trọng trong vật lý và kỹ thuật điện. Khi nhiệt độ của vật liệu thay đổi, các đặc tính của vật liệu cũng thay đổi, dẫn đến sự thay đổi của điện trở. Đối với các vật liệu kim loại, khi nhiệt độ tăng, các nguyên tử trong kim loại dao động mạnh hơn, cản trở sự di chuyển của các electron tự do, từ đó làm tăng điện trở.
Để biểu diễn sự phụ thuộc này, chúng ta sử dụng công thức sau:
\[
R = R_0 \left[ 1 + \alpha (t - t_0) \right]
\]
- \(R\) là điện trở tại nhiệt độ \(t\).
- \(R_0\) là điện trở tại nhiệt độ chuẩn \(t_0\) (thường là 20°C hoặc 25°C).
- \(\alpha\) là hệ số nhiệt điện trở, biểu thị mức độ thay đổi điện trở theo nhiệt độ.
- \(t\) là nhiệt độ hiện tại của vật liệu.
- \(t_0\) là nhiệt độ chuẩn.
Điện trở của vật liệu sẽ tăng hoặc giảm phụ thuộc vào hệ số nhiệt điện trở \(\alpha\). Đối với hầu hết các kim loại, \(\alpha\) là dương, nghĩa là điện trở tăng khi nhiệt độ tăng. Tuy nhiên, với một số vật liệu bán dẫn hoặc chất điện trở đặc biệt, \(\alpha\) có thể âm, dẫn đến điện trở giảm khi nhiệt độ tăng.
2. Công thức tính điện trở phụ thuộc nhiệt độ cơ bản
Công thức tính điện trở phụ thuộc nhiệt độ cơ bản là một công cụ quan trọng trong vật lý và kỹ thuật điện tử. Công thức này cho phép tính toán sự thay đổi của điện trở khi nhiệt độ thay đổi, đặc biệt hữu ích trong việc thiết kế và phân tích các mạch điện chịu ảnh hưởng của nhiệt độ.
Công thức cơ bản được sử dụng để tính điện trở \( R \) tại nhiệt độ \( t \) từ điện trở \( R_0 \) tại một nhiệt độ chuẩn \( t_0 \) như sau:
\[
R = R_0 \left[ 1 + \alpha (t - t_0) \right]
\]
- \(R\) là điện trở của vật liệu tại nhiệt độ \( t \) (đơn vị: Ohm).
- \(R_0\) là điện trở của vật liệu tại nhiệt độ chuẩn \( t_0 \) (thường là 20°C hoặc 25°C, đơn vị: Ohm).
- \(\alpha\) là hệ số nhiệt điện trở của vật liệu, có đơn vị là \(1/°C\), thể hiện mức độ thay đổi của điện trở theo nhiệt độ.
- \(t\) là nhiệt độ cần tính điện trở (đơn vị: °C).
- \(t_0\) là nhiệt độ chuẩn (đơn vị: °C).
Hệ số nhiệt điện trở \(\alpha\) thường có giá trị dương đối với kim loại, điều này có nghĩa là điện trở sẽ tăng khi nhiệt độ tăng. Đối với các vật liệu bán dẫn, \(\alpha\) có thể âm, tức là điện trở giảm khi nhiệt độ tăng.
Ví dụ, nếu ta biết điện trở \(R_0\) của một dây dẫn bằng đồng tại nhiệt độ chuẩn \(t_0\) là 100 Ohm và hệ số nhiệt điện trở \(\alpha\) là \(0.004/°C\), chúng ta có thể tính điện trở tại nhiệt độ \(t = 50°C\) như sau:
\[
R = 100 \times \left[ 1 + 0.004 \times (50 - 20) \right] = 100 \times 1.12 = 112 \, \text{Ohm}
\]
Điều này có nghĩa là khi nhiệt độ tăng từ 20°C lên 50°C, điện trở của dây dẫn tăng từ 100 Ohm lên 112 Ohm.
Công thức này là nền tảng cho nhiều ứng dụng thực tiễn, từ việc thiết kế mạch điện tử đến kiểm soát nhiệt độ trong các hệ thống công nghiệp.

3. Công thức nâng cao cho các vật liệu đặc biệt
Trong lĩnh vực điện tử, công thức tính điện trở phụ thuộc nhiệt độ của các vật liệu đặc biệt như thermistor, đặc biệt là loại NTC (Negative Temperature Coefficient) và PTC (Positive Temperature Coefficient), được sử dụng rộng rãi để đo lường và kiểm soát nhiệt độ. Các công thức nâng cao này được thiết kế để mô tả chính xác hơn sự biến đổi điện trở của các vật liệu không phải kim loại khi nhiệt độ thay đổi.
3.1. Công thức cho cảm biến nhiệt độ RTD
Đối với các cảm biến nhiệt độ RTD (Resistance Temperature Detector), thường sử dụng vật liệu bạch kim do tính ổn định và độ chính xác cao. Công thức cơ bản của RTD là:
Trong đó:
- R(T) là điện trở tại nhiệt độ T.
- R_0 là điện trở tại nhiệt độ tham chiếu \( T_0 \) (thường là 0°C).
- \(\alpha\) là hệ số nhiệt điện trở của vật liệu.
- T là nhiệt độ hiện tại.
Công thức này chỉ đúng trong khoảng nhiệt độ nhất định và chủ yếu dành cho kim loại như bạch kim, thường được dùng trong các ứng dụng yêu cầu độ chính xác cao, như trong các thiết bị đo lường công nghiệp.
3.2. Các yếu tố ảnh hưởng đến công thức nâng cao
Đối với các vật liệu phi kim loại như thermistor, sự phụ thuộc điện trở vào nhiệt độ có thể phức tạp hơn, do đó cần các công thức nâng cao hơn để tính toán. Với NTC thermistor, công thức phổ biến được sử dụng là:
Trong đó:
- R(T) là điện trở tại nhiệt độ T (đơn vị Kelvin).
- R_{\infty} là điện trở tại một giá trị rất cao của nhiệt độ.
- B là hằng số vật liệu đặc trưng (được xác định qua thực nghiệm).
Công thức này giúp mô tả sự giảm mạnh của điện trở khi nhiệt độ tăng, đặc trưng cho các loại NTC thermistor. Đối với PTC thermistor, khi vượt quá một nhiệt độ nhất định (nhiệt độ Curie), điện trở sẽ tăng đột ngột, đòi hỏi công thức điều chỉnh riêng.
3.3. Bảng tra cứu điện trở theo nhiệt độ
Trong thực tế, để tiện lợi hơn cho việc tính toán và sử dụng, người ta thường sử dụng các bảng tra cứu giá trị điện trở theo nhiệt độ cho các loại thermistor. Các bảng này được xây dựng dựa trên các công thức lý thuyết, nhưng điều chỉnh để phù hợp với thực tế sản xuất và ứng dụng của từng loại vật liệu.
Việc sử dụng bảng tra cứu giúp giảm thiểu sai sót trong tính toán, đồng thời cho phép nhanh chóng xác định điện trở của cảm biến tại bất kỳ nhiệt độ nào trong phạm vi hoạt động.
4. Ứng dụng của công thức tính điện trở phụ thuộc nhiệt độ trong công nghiệp
Công thức tính điện trở phụ thuộc nhiệt độ được ứng dụng rộng rãi trong nhiều lĩnh vực công nghiệp, nhờ khả năng kiểm soát và điều chỉnh nhiệt độ một cách chính xác. Dưới đây là một số ứng dụng nổi bật:
4.1. Ứng dụng trong các thiết bị đo nhiệt độ
Trong các thiết bị đo nhiệt độ như cảm biến RTD (Resistance Temperature Detector), ví dụ như PT100, công thức tính điện trở theo nhiệt độ được sử dụng để xác định nhiệt độ môi trường xung quanh. Điện trở của RTD thay đổi theo nhiệt độ, và thông qua đó, nhiệt độ có thể được đo lường một cách chính xác. Công thức chính cho PT100 là:
\[
R_t = R_0 \times (1 + A \times T + B \times T^2 + C \times (T-100) \times T^3)
\]
Trong đó:
- \(R_t\): Điện trở tại nhiệt độ \(T\) (°C).
- \(R_0\): Điện trở tại nhiệt độ tham chiếu (thường là 0°C, với \(R_0\) = 100Ω cho PT100).
- \(A\), \(B\), \(C\): Các hệ số cụ thể cho từng loại cảm biến.
Cảm biến PT100 được sử dụng rộng rãi trong các hệ thống đo nhiệt độ công nghiệp nhờ độ chính xác cao và khả năng ổn định trong môi trường khắc nghiệt.
4.2. Ứng dụng trong thiết kế mạch điện tử
Điện trở nhiệt (Thermistors) với các hệ số nhiệt độ âm (NTC) và dương (PTC) cũng là một phần quan trọng trong các thiết kế mạch điện tử. NTC thường được sử dụng trong các mạch bảo vệ quá nhiệt hoặc điều khiển nhiệt độ, trong khi PTC được dùng trong các ứng dụng bảo vệ dòng quá tải hoặc tự động điều chỉnh nhiệt độ.
Ví dụ, trong một mạch bảo vệ quá nhiệt, một NTC sẽ giảm giá trị điện trở khi nhiệt độ tăng, kích hoạt cơ chế bảo vệ để ngắt dòng điện hoặc giảm công suất nhằm tránh hư hỏng thiết bị.
4.3. Ứng dụng trong các hệ thống động cơ và thiết bị công suất
Trong các hệ thống động cơ và thiết bị công suất, các điện trở nhiệt PTC thường được tích hợp để bảo vệ khỏi quá tải nhiệt. Khi nhiệt độ của thiết bị tăng đến mức nguy hiểm, điện trở của PTC tăng đột ngột, giới hạn dòng điện và bảo vệ thiết bị khỏi hư hại.
Việc sử dụng công thức tính điện trở phụ thuộc nhiệt độ trong thiết kế và điều khiển nhiệt độ giúp tăng cường hiệu quả hoạt động và tuổi thọ của các hệ thống công nghiệp, đồng thời đảm bảo an toàn cho quá trình vận hành.

5. So sánh các phương pháp tính điện trở theo nhiệt độ
Trong phần này, chúng ta sẽ tiến hành so sánh hai phương pháp tính điện trở theo nhiệt độ chính, bao gồm phương pháp cơ bản và phương pháp nâng cao. Việc so sánh này sẽ giúp làm rõ sự khác biệt giữa các phương pháp và giúp xác định khi nào nên sử dụng từng phương pháp.
5.1. Phương pháp cơ bản vs. phương pháp nâng cao
- Phương pháp cơ bản: Công thức tính điện trở theo nhiệt độ dựa trên sự thay đổi tuyến tính của điện trở với nhiệt độ, được mô tả bởi công thức:
\[
R(T) = R_0(1 + \alpha(T - T_0))
\]
Trong đó:
- \(R(T)\): Điện trở tại nhiệt độ \(T\)
- \(R_0\): Điện trở tại nhiệt độ tham chiếu \(T_0\)
- \(\alpha\): Hệ số nhiệt điện trở
- Phương pháp nâng cao: Dành cho các vật liệu đặc biệt hoặc các điều kiện phi tuyến tính. Phương pháp này sử dụng các mô hình toán học phức tạp hơn hoặc bảng tra cứu cụ thể cho từng loại vật liệu. Một ví dụ phổ biến là công thức dành cho cảm biến nhiệt độ RTD, bao gồm các hằng số phức tạp hơn để mô tả mối quan hệ giữa nhiệt độ và điện trở.
5.2. Độ chính xác của các phương pháp
Phương pháp cơ bản thường đơn giản và dễ áp dụng, phù hợp cho các trường hợp mà sự thay đổi điện trở theo nhiệt độ gần như tuyến tính, ví dụ như trong trường hợp của các kim loại ở một khoảng nhiệt độ nhỏ.
Phương pháp nâng cao có độ chính xác cao hơn, đặc biệt khi áp dụng cho các vật liệu có tính chất nhiệt điện trở phức tạp hoặc trong các ứng dụng yêu cầu độ chính xác cao, chẳng hạn như trong các hệ thống cảm biến công nghiệp.
5.3. Khi nào nên sử dụng từng phương pháp?
- Phương pháp cơ bản: Nên sử dụng khi cần tính toán nhanh, yêu cầu không quá cao về độ chính xác, và khi làm việc với các vật liệu có tính chất điện trở thay đổi tuyến tính với nhiệt độ.
- Phương pháp nâng cao: Nên áp dụng trong các ứng dụng công nghiệp, nơi đòi hỏi độ chính xác cao, hoặc khi làm việc với các vật liệu đặc biệt có hệ số nhiệt điện trở phi tuyến tính.








.png)