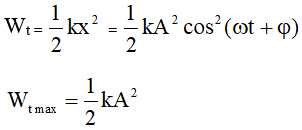Chủ đề công thức động năng thế năng: Công thức động năng thế năng là nền tảng quan trọng trong vật lý học, giúp hiểu rõ về năng lượng trong các hệ cơ học. Bài viết này cung cấp hướng dẫn chi tiết về các công thức và ứng dụng thực tế, giúp bạn nắm vững kiến thức và áp dụng hiệu quả trong học tập và cuộc sống.
Mục lục
Công Thức Động Năng Và Thế Năng
Trong vật lý học, động năng và thế năng là hai khái niệm quan trọng liên quan đến năng lượng cơ học. Dưới đây là tổng hợp chi tiết về các công thức liên quan đến động năng và thế năng, cùng với các ví dụ minh họa.
1. Động Năng
Động năng là năng lượng mà một vật có được do nó đang chuyển động. Công thức tính động năng của một vật được biểu diễn như sau:
Trong đó:
- Wd: Động năng (đơn vị: Joule - J).
- m: Khối lượng của vật (kg).
- v: Vận tốc của vật (m/s).
2. Thế Năng
Thế năng là năng lượng tiềm tàng của một vật khi nó nằm ở một vị trí nhất định trong trường trọng lực hoặc trường lực khác. Có hai loại thế năng chính:
- Thế năng hấp dẫn: Thế năng này liên quan đến vị trí của vật trong trường trọng lực.
- Thế năng đàn hồi: Thế năng này liên quan đến sự biến dạng của lò xo hoặc vật đàn hồi.
2.1. Thế Năng Hấp Dẫn
Công thức tính thế năng hấp dẫn của một vật ở độ cao h trong trường trọng lực:
Trong đó:
- Wt: Thế năng hấp dẫn (đơn vị: Joule - J).
- g: Gia tốc trọng trường (khoảng 9,81 m/s² trên Trái Đất).
- h: Độ cao của vật so với mốc chọn làm gốc thế năng (m).
2.2. Thế Năng Đàn Hồi
Thế năng đàn hồi của một lò xo được tính bằng công thức:
Trong đó:
- Wd: Thế năng đàn hồi (Joule - J).
- k: Hằng số đàn hồi của lò xo (N/m).
- x: Độ biến dạng của lò xo so với vị trí cân bằng (m).
3. Định Luật Bảo Toàn Cơ Năng
Trong hệ cô lập (không có lực ngoài tác dụng), tổng động năng và thế năng của hệ là một hằng số. Điều này được biểu diễn bằng định luật bảo toàn cơ năng:
Trong đó:
- Wd: Động năng của vật.
- Wt: Thế năng của vật.
- C: Hằng số, tổng cơ năng của hệ.
Ví dụ, trong quá trình một vật rơi tự do, thế năng của nó giảm dần trong khi động năng tăng lên, nhưng tổng cơ năng của vật luôn được bảo toàn.
4. Bài Tập Vận Dụng
Dưới đây là một số bài tập vận dụng về động năng và thế năng:
| Bài Tập | Lời Giải |
|---|---|
| Bài Tập 1: Một vật có khối lượng 2kg đang chuyển động với vận tốc 3m/s. Tính động năng của vật. | |
| Bài Tập 2: Một vật có khối lượng 1kg được đặt ở độ cao 5m so với mặt đất. Tính thế năng hấp dẫn của vật. |

.png)
Mục Lục Tổng Hợp
Trong bài viết này, chúng ta sẽ khám phá chi tiết các khái niệm, công thức, và ứng dụng của động năng và thế năng, từ những nguyên lý cơ bản cho đến những bài tập vận dụng nâng cao.
- Tổng Quan Về Động Năng Và Thế Năng
- Định nghĩa động năng
- Định nghĩa thế năng
- Công Thức Tính Động Năng
- Công thức động năng
- Ví dụ tính động năng
- Công Thức Tính Thế Năng
- Thế năng hấp dẫn
- Thế năng đàn hồi
- Định Luật Bảo Toàn Cơ Năng
- Công thức bảo toàn cơ năng
- Ứng dụng của định luật bảo toàn cơ năng
- Bài Tập Vận Dụng Về Động Năng Và Thế Năng
- Bài tập tính động năng
- Bài tập tính thế năng
- Bài tập bảo toàn cơ năng
1. Tổng Quan Về Động Năng Và Thế Năng
Động năng và thế năng là hai khái niệm cơ bản trong vật lý học, đặc biệt là trong lĩnh vực cơ học. Cả hai đều là dạng của năng lượng và đóng vai trò quan trọng trong việc mô tả các hiện tượng vật lý liên quan đến chuyển động và vị trí của vật.
Động Năng
Động năng là dạng năng lượng mà một vật có được nhờ vào chuyển động của nó. Công thức tính động năng là:
$$W_{đ} = \frac{1}{2} m v^2$$
Trong đó:
- $$W_{đ}$$: Động năng (đơn vị là Joule, J)
- $$m$$: Khối lượng của vật (kg)
- $$v$$: Vận tốc của vật (m/s)
Thế Năng
Thế năng là dạng năng lượng mà một vật có được do vị trí của nó trong một trường lực (ví dụ như trường trọng lực). Thế năng có thể được tính bằng công thức:
$$W_t = mgh$$
Trong đó:
- $$W_t$$: Thế năng (đơn vị là Joule, J)
- $$m$$: Khối lượng của vật (kg)
- $$g$$: Gia tốc trọng trường (≈9.81 m/s²)
- $$h$$: Độ cao của vật so với mốc chọn (m)
Mối Quan Hệ Giữa Động Năng và Thế Năng
Cả động năng và thế năng đều là các thành phần của cơ năng, tổng năng lượng cơ học của một hệ thống. Khi một vật chuyển động, thế năng của nó có thể chuyển đổi thành động năng và ngược lại, tùy thuộc vào vị trí và tốc độ của vật. Tổng cơ năng của một hệ cô lập không thay đổi, nó chỉ biến đổi từ dạng này sang dạng khác theo định luật bảo toàn cơ năng.

2. Công Thức Tính Động Năng
Động năng là dạng năng lượng mà một vật sở hữu do chuyển động của nó. Động năng phụ thuộc vào khối lượng của vật và vận tốc của nó. Công thức tính động năng có dạng:
$$W_{đ} = \frac{1}{2} m v^2$$
Trong đó:
- $$W_{đ}$$: Động năng của vật (đơn vị là Joule, J)
- $$m$$: Khối lượng của vật (kg)
- $$v$$: Vận tốc của vật (m/s)
Cách Sử Dụng Công Thức Tính Động Năng
Để tính động năng của một vật, bạn cần biết khối lượng và vận tốc của nó:
- Đầu tiên, xác định khối lượng của vật. Ví dụ, nếu khối lượng là 5 kg, bạn sử dụng $$m = 5$$.
- Tiếp theo, đo vận tốc của vật. Nếu vận tốc là 10 m/s, bạn sử dụng $$v = 10$$.
- Áp dụng công thức: $$W_{đ} = \frac{1}{2} \times 5 \times (10)^2 = 250 \text{ J}$$
Ví Dụ Tính Động Năng
Giả sử bạn có một vật nặng 2 kg di chuyển với vận tốc 3 m/s. Động năng của vật này được tính như sau:
$$W_{đ} = \frac{1}{2} \times 2 \times (3)^2 = 9 \text{ J}$$
Ứng Dụng Của Động Năng Trong Đời Sống
Động năng xuất hiện trong nhiều tình huống thực tế, như khi một chiếc xe đang di chuyển, khi một viên đạn được bắn ra hoặc khi một quả bóng đang lăn. Tính toán động năng giúp chúng ta hiểu được năng lượng cần thiết để thực hiện một hành động cụ thể, cũng như dự đoán kết quả của những chuyển động đó.
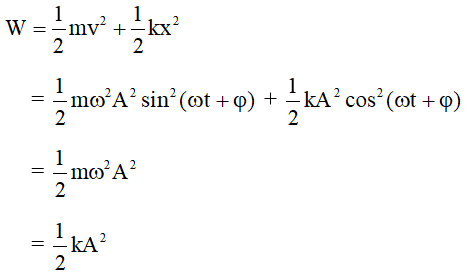
XEM THÊM:
3. Công Thức Tính Thế Năng
Thế năng là dạng năng lượng mà một vật có được do vị trí của nó trong một trường lực, chẳng hạn như trọng trường hoặc điện trường. Công thức tính thế năng trọng trường phụ thuộc vào khối lượng của vật, độ cao so với một mốc và gia tốc trọng trường.
Công thức tính thế năng trọng trường:
$$W_t = mgh$$
Trong đó:
- $$W_t$$: Thế năng (đơn vị là Joule, J)
- $$m$$: Khối lượng của vật (kg)
- $$g$$: Gia tốc trọng trường (≈9.81 m/s²)
- $$h$$: Độ cao của vật so với mốc chọn (m)
Cách Sử Dụng Công Thức Tính Thế Năng
Để tính thế năng của một vật, bạn cần làm theo các bước sau:
- Đầu tiên, xác định khối lượng của vật. Ví dụ, nếu khối lượng là 10 kg, bạn sử dụng $$m = 10$$.
- Tiếp theo, đo độ cao của vật so với mốc chọn. Nếu độ cao là 5 m, bạn sử dụng $$h = 5$$.
- Áp dụng gia tốc trọng trường $$g ≈ 9.81$$ m/s².
- Áp dụng công thức: $$W_t = 10 \times 9.81 \times 5 = 490.5 \text{ J}$$
Ví Dụ Tính Thế Năng
Giả sử bạn có một vật nặng 2 kg được đặt ở độ cao 3 m so với mặt đất. Thế năng của vật này sẽ được tính như sau:
$$W_t = 2 \times 9.81 \times 3 = 58.86 \text{ J}$$
Ứng Dụng Của Thế Năng Trong Đời Sống
Thế năng có mặt trong nhiều hiện tượng hàng ngày, chẳng hạn như khi bạn nâng một vật lên cao, quả bóng được đặt trên bàn, hay nước trong hồ chứa trên núi. Việc hiểu rõ thế năng giúp chúng ta tính toán được công cần thiết để nâng vật và phân tích chuyển động của các vật thể trong các hệ thống phức tạp hơn.

4. Định Luật Bảo Toàn Cơ Năng
Định luật bảo toàn cơ năng là một nguyên lý quan trọng trong vật lý, khẳng định rằng tổng cơ năng của một hệ cô lập không thay đổi theo thời gian, mà chỉ chuyển đổi giữa các dạng năng lượng như động năng và thế năng. Điều này có nghĩa là khi một vật chuyển động trong một hệ thống không có lực ma sát hay lực cản, tổng động năng và thế năng của vật luôn không đổi.
Phát Biểu Định Luật
Định luật bảo toàn cơ năng có thể được phát biểu như sau: "Trong một hệ kín, không có ma sát, tổng cơ năng (động năng và thế năng) của vật là không đổi."
Công Thức Toán Học
Định luật bảo toàn cơ năng có thể biểu diễn bằng công thức sau:
$$W_{đ1} + W_{t1} = W_{đ2} + W_{t2}$$
Trong đó:
- $$W_{đ1}$$: Động năng ban đầu
- $$W_{t1}$$: Thế năng ban đầu
- $$W_{đ2}$$: Động năng tại thời điểm sau
- $$W_{t2}$$: Thế năng tại thời điểm sau
Ứng Dụng Của Định Luật Bảo Toàn Cơ Năng
Định luật bảo toàn cơ năng được áp dụng rộng rãi trong nhiều lĩnh vực như cơ học, thiên văn học, và công nghệ. Ví dụ:
- Trong chuyển động con lắc đơn, khi con lắc ở vị trí cao nhất, thế năng đạt cực đại và động năng bằng không; khi con lắc đi qua vị trí cân bằng, động năng đạt cực đại và thế năng bằng không.
- Trong chuyển động của các hành tinh quanh mặt trời, động năng và thế năng của hành tinh thay đổi liên tục, nhưng tổng cơ năng vẫn không đổi.
Ví Dụ Cụ Thể
Giả sử một vật nặng rơi từ độ cao 10 m xuống đất. Ban đầu, khi ở trên cao, vật có thế năng lớn và động năng bằng không. Khi vật rơi, thế năng giảm dần và động năng tăng lên. Tại thời điểm chạm đất, toàn bộ thế năng đã chuyển thành động năng. Theo định luật bảo toàn cơ năng, tổng năng lượng của vật trước và sau khi rơi vẫn giữ nguyên.
5. Bài Tập Vận Dụng Về Động Năng Và Thế Năng
Dưới đây là một số bài tập vận dụng về động năng và thế năng kèm theo lời giải chi tiết. Các bài tập này giúp bạn củng cố kiến thức và làm quen với các dạng bài liên quan đến động năng và thế năng.
5.1. Bài Tập Tính Động Năng
- Bài tập 1: Một vật có khối lượng m = 2 kg đang chuyển động với vận tốc v = 5 m/s. Tính động năng của vật.
- Lời giải:
- Bài tập 2: Một ô tô có khối lượng m = 1000 kg đang chuyển động với vận tốc v = 72 km/h. Tính động năng của ô tô (biết 1 m/s = 3.6 km/h).
- Lời giải:
Động năng của vật được tính theo công thức:
\[ W_d = \frac{1}{2}mv^2 \]
Thay số vào ta có:
\[ W_d = \frac{1}{2} \times 2 \times 5^2 = 25 \text{ J} \]
Trước tiên, ta đổi vận tốc từ km/h sang m/s:
\[ v = \frac{72}{3.6} = 20 \text{ m/s} \]
Sau đó, áp dụng công thức tính động năng:
\[ W_d = \frac{1}{2} \times 1000 \times 20^2 = 200,000 \text{ J} \]
5.2. Bài Tập Tính Thế Năng
- Bài tập 1: Một vật có khối lượng m = 5 kg được đặt ở độ cao h = 10 m so với mặt đất. Tính thế năng trọng trường của vật. Lấy g = 9.8 m/s^2.
- Lời giải:
- Bài tập 2: Một lò xo có độ cứng k = 200 N/m bị nén một đoạn x = 0.1 m. Tính thế năng đàn hồi của lò xo.
- Lời giải:
Thế năng trọng trường được tính theo công thức:
\[ W_t = mgh \]
Thay số vào ta có:
\[ W_t = 5 \times 9.8 \times 10 = 490 \text{ J} \]
Thế năng đàn hồi được tính theo công thức:
\[ W_t = \frac{1}{2}kx^2 \]
Thay số vào ta có:
\[ W_t = \frac{1}{2} \times 200 \times 0.1^2 = 1 \text{ J} \]
5.3. Bài Tập Bảo Toàn Cơ Năng
- Bài tập 1: Một vật có khối lượng m = 2 kg được thả rơi tự do từ độ cao h = 20 m. Bỏ qua lực cản không khí, tính vận tốc của vật khi chạm đất. Lấy g = 9.8 m/s^2.
- Lời giải:
- Bài tập 2: Một vật lăn từ đỉnh dốc cao h = 15 m. Tính vận tốc của vật ở chân dốc, biết rằng mọi năng lượng chuyển hóa thành động năng.
- Lời giải:
Sử dụng định luật bảo toàn cơ năng:
\[ W_t = W_d \]
Áp dụng công thức:
\[ mgh = \frac{1}{2}mv^2 \]
Giải phương trình để tìm vận tốc v:
\[ v = \sqrt{2gh} = \sqrt{2 \times 9.8 \times 20} \approx 19.8 \text{ m/s} \]
Sử dụng định luật bảo toàn cơ năng:
\[ mgh = \frac{1}{2}mv^2 \]
Giải để tìm vận tốc v:
\[ v = \sqrt{2gh} = \sqrt{2 \times 9.8 \times 15} \approx 17.15 \text{ m/s} \]