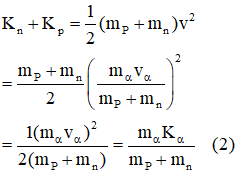Chủ đề độ biến thiên động năng: Độ biến thiên động năng là một khái niệm quan trọng trong vật lý, liên quan mật thiết đến sự thay đổi của công cơ học. Bài viết này sẽ giúp bạn hiểu rõ hơn về độ biến thiên động năng, các yếu tố ảnh hưởng, ứng dụng thực tiễn trong đời sống và cung cấp các bài tập minh họa để củng cố kiến thức.
Mục lục
- Ví Dụ Thực Tế Về Độ Biến Thiên Động Năng
- I. Khái Niệm Độ Biến Thiên Động Năng
- II. Mối Quan Hệ Giữa Công và Độ Biến Thiên Động Năng
- III. Các Yếu Tố Ảnh Hưởng Đến Độ Biến Thiên Động Năng
- IV. Ứng Dụng Thực Tiễn Của Độ Biến Thiên Động Năng
- V. Bài Tập Vận Dụng Về Độ Biến Thiên Động Năng
- VI. Tổng Kết Và Kết Luận
Ví Dụ Thực Tế Về Độ Biến Thiên Động Năng
Hãy xem xét một chiếc ô tô có khối lượng 1000 kg di chuyển trên đường. Khi tài xế nhấn ga, vận tốc của ô tô tăng từ 20 m/s lên 30 m/s. Chúng ta có thể tính độ biến thiên động năng của ô tô trong quá trình tăng tốc này.
Động năng ban đầu của ô tô khi vận tốc là 20 m/s:
Động năng cuối cùng của ô tô khi vận tốc đạt 30 m/s:
Độ biến thiên động năng của ô tô trong quá trình này là:
Điều này có nghĩa là ô tô đã nhận thêm 250,000 J năng lượng từ động cơ trong quá trình tăng tốc.
Ví dụ này minh họa cách độ biến thiên động năng được áp dụng trong thực tế, từ đó giúp chúng ta hiểu rõ hơn về quá trình chuyển động và năng lượng của các phương tiện giao thông.

.png)
I. Khái Niệm Độ Biến Thiên Động Năng
Độ biến thiên động năng là khái niệm quan trọng trong vật lý học, biểu thị sự thay đổi của động năng của một vật khi nó chuyển động dưới tác dụng của lực. Để hiểu rõ hơn về khái niệm này, ta cần nắm vững một số định nghĩa cơ bản:
- Động năng: Động năng là năng lượng mà một vật có được do chuyển động của nó. Công thức tính động năng của một vật có khối lượng \(m\) và vận tốc \(v\) là: \[ K = \frac{1}{2}mv^2 \]
- Độ biến thiên động năng: Độ biến thiên động năng (ký hiệu là \(\Delta K\)) là sự chênh lệch giữa động năng ban đầu và động năng sau cùng của vật trong quá trình chuyển động. Công thức tính độ biến thiên động năng là:
\[
\Delta K = K_{\text{cuối}} - K_{\text{đầu}}
\]
Trong đó:
- \(K_{\text{cuối}}\): Động năng tại thời điểm sau cùng.
- \(K_{\text{đầu}}\): Động năng tại thời điểm ban đầu.
Độ biến thiên động năng có thể dương, âm hoặc bằng không, tùy thuộc vào việc vật tăng tốc, giảm tốc hay giữ nguyên vận tốc. Điều này tương ứng với việc công thực hiện bởi các lực tác dụng lên vật là dương, âm hoặc bằng không.
| Trường hợp | Độ biến thiên động năng | Giải thích |
| Vật tăng tốc | \(\Delta K > 0\) | Động năng tăng, vật nhận thêm năng lượng từ công của lực tác dụng. |
| Vật giảm tốc | \(\Delta K < 0\) | Động năng giảm, một phần năng lượng của vật bị mất đi do công của lực cản. |
| Vật giữ nguyên vận tốc | \(\Delta K = 0\) | Động năng không đổi, tổng công thực hiện bằng không. |
II. Mối Quan Hệ Giữa Công và Độ Biến Thiên Động Năng
Mối quan hệ giữa công và độ biến thiên động năng được biểu diễn thông qua định lý công - động năng. Định lý này nêu rõ rằng công thực hiện bởi tổng các lực tác dụng lên một vật trong quá trình chuyển động bằng với độ biến thiên động năng của vật đó. Điều này được diễn đạt bằng công thức:
Trong đó:
- W: Công thực hiện bởi lực, đơn vị đo là Joule (J).
- \(\Delta K\): Độ biến thiên động năng của vật, tính bằng Joule (J).
Để hiểu rõ hơn, ta xét các bước tính toán cụ thể:
- Tính công của lực tác dụng: Công \(W\) được tính bằng tích của lực \(F\) và quãng đường \(d\) mà lực này tác dụng theo hướng chuyển động của vật:
\[
W = F \cdot d \cdot \cos{\theta}
\]
Trong đó:
- \(F\): Lực tác dụng lên vật (Newton - N).
- \(d\): Quãng đường vật di chuyển (mét - m).
- \(\theta\): Góc giữa hướng lực và hướng di chuyển của vật.
- Tính độ biến thiên động năng: Từ công thức động năng, ta có:
\[
\Delta K = \frac{1}{2}m(v_2^2 - v_1^2)
\]
Trong đó:
- \(m\): Khối lượng của vật (kg).
- \(v_1\): Vận tốc ban đầu của vật (m/s).
- \(v_2\): Vận tốc sau cùng của vật (m/s).
Như vậy, nếu công thực hiện lên vật là dương, độ biến thiên động năng sẽ dương, nghĩa là vật tăng tốc. Ngược lại, nếu công là âm, độ biến thiên động năng sẽ âm, tức là vật giảm tốc.
| Trường hợp | Công \(W\) | \(\Delta K\) | Kết quả |
| Lực kéo cùng hướng chuyển động | Dương | Dương | Vật tăng tốc |
| Lực cản ngược hướng chuyển động | Âm | Âm | Vật giảm tốc |
| Không có lực tác dụng | 0 | 0 | Vật giữ nguyên vận tốc |

III. Các Yếu Tố Ảnh Hưởng Đến Độ Biến Thiên Động Năng
Độ biến thiên động năng của một vật phụ thuộc vào nhiều yếu tố khác nhau. Dưới đây là các yếu tố chính ảnh hưởng đến độ biến thiên động năng:
1. Ảnh hưởng của khối lượng
Khối lượng của vật là một trong những yếu tố quan trọng nhất ảnh hưởng đến động năng của vật. Động năng được tính bằng công thức:
\( W_{đ} = \frac{1}{2} m v^2 \)
Trong đó:
- \(W_{đ}\) là động năng của vật (J)
- \(m\) là khối lượng của vật (kg)
- \(v\) là vận tốc của vật (m/s)
Rõ ràng, khi khối lượng của vật tăng, động năng của vật cũng tăng nếu vận tốc của vật không thay đổi. Ngược lại, nếu khối lượng giảm, động năng của vật sẽ giảm.
2. Ảnh hưởng của vận tốc
Vận tốc là yếu tố thứ hai có ảnh hưởng lớn đến độ biến thiên động năng. Từ công thức tính động năng, ta thấy rằng động năng tỉ lệ thuận với bình phương của vận tốc:
\( W_{đ} \propto v^2 \)
Điều này có nghĩa là, khi vận tốc của vật tăng gấp đôi, động năng của vật sẽ tăng lên gấp bốn lần. Ngược lại, nếu vận tốc giảm một nửa, động năng sẽ giảm xuống còn một phần tư.
3. Các yếu tố ngoại cảnh khác
Bên cạnh khối lượng và vận tốc, các yếu tố ngoại cảnh như lực cản, ma sát, và tác động của ngoại lực cũng ảnh hưởng đến độ biến thiên động năng. Ví dụ, khi một vật chuyển động trong môi trường có lực cản lớn (như không khí hoặc nước), động năng của vật sẽ giảm nhanh chóng hơn do công của lực cản. Ngược lại, khi ngoại lực tác động lên vật và sinh công dương (như khi đẩy hoặc kéo vật), động năng của vật sẽ tăng lên.
Một yếu tố quan trọng khác là hệ quy chiếu. Động năng của một vật có thể thay đổi tùy thuộc vào hệ quy chiếu mà ta lựa chọn. Trong một hệ quy chiếu mà tổng động lượng của hệ bằng không, giá trị động năng sẽ đạt giá trị nhỏ nhất.
Như vậy, độ biến thiên động năng của một vật là kết quả của sự tương tác phức tạp giữa các yếu tố nội tại của vật (như khối lượng và vận tốc) và các yếu tố ngoại cảnh (như lực cản và ngoại lực). Hiểu rõ các yếu tố này giúp ta có thể dự đoán và điều chỉnh động năng của vật trong các ứng dụng thực tiễn.

XEM THÊM:
IV. Ứng Dụng Thực Tiễn Của Độ Biến Thiên Động Năng
Độ biến thiên động năng là một khái niệm quan trọng trong vật lý, có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật. Dưới đây là một số ứng dụng tiêu biểu:
1. Ứng dụng trong kỹ thuật
Trong kỹ thuật, độ biến thiên động năng được sử dụng để thiết kế và tối ưu hóa các hệ thống cơ học, đặc biệt là trong lĩnh vực ô tô, hàng không, và cơ khí.
- Thiết kế phanh xe: Phanh xe hoạt động dựa trên nguyên lý chuyển động năng của xe thành nhiệt năng thông qua ma sát. Độ biến thiên động năng giúp xác định lực cần thiết để dừng xe trong một khoảng cách nhất định.
- Các hệ thống giảm chấn: Trong các hệ thống giảm chấn của xe cộ và máy móc, độ biến thiên động năng giúp xác định lượng năng lượng được hấp thụ và phân tán, từ đó cải thiện độ an toàn và hiệu quả hoạt động của thiết bị.
2. Ứng dụng trong đời sống
Trong đời sống hàng ngày, khái niệm độ biến thiên động năng cũng được ứng dụng rộng rãi trong các thiết bị và hoạt động thông thường.
- Thể thao: Trong các môn thể thao như bóng đá, bóng rổ, hay quần vợt, vận động viên sử dụng khái niệm này để kiểm soát tốc độ và hướng di chuyển của bóng, từ đó đạt được hiệu suất cao nhất.
- Thiết bị gia dụng: Các thiết bị như máy giặt và máy quay ly tâm cũng hoạt động dựa trên nguyên lý biến thiên động năng, giúp tiết kiệm năng lượng và nâng cao hiệu quả sử dụng.
3. Các thí nghiệm liên quan
Trong giáo dục và nghiên cứu, các thí nghiệm liên quan đến độ biến thiên động năng giúp học sinh và sinh viên hiểu rõ hơn về nguyên lý hoạt động của các hiện tượng vật lý.
- Thí nghiệm con lắc đơn: Sử dụng con lắc đơn để đo lường độ biến thiên động năng và xác định mối quan hệ giữa động năng và thế năng.
- Thí nghiệm va chạm: Các thí nghiệm về va chạm đàn hồi và không đàn hồi giúp nghiên cứu sự chuyển đổi giữa các dạng năng lượng và ứng dụng trong thiết kế các hệ thống an toàn như túi khí và các cấu trúc chịu va đập.

V. Bài Tập Vận Dụng Về Độ Biến Thiên Động Năng
Dưới đây là một số bài tập vận dụng về độ biến thiên động năng giúp các bạn học sinh củng cố kiến thức và kỹ năng tính toán trong môn Vật lý.
1. Bài tập cơ bản
- Bài 1: Một vật có khối lượng 2 kg chuyển động với vận tốc ban đầu là 5 m/s. Tính động năng của vật tại thời điểm ban đầu và sau khi vận tốc tăng lên 10 m/s.
- Bài 2: Một vật có khối lượng 1 kg chuyển động dưới tác dụng của một lực không đổi làm tăng vận tốc của nó từ 2 m/s lên 6 m/s. Tính độ biến thiên động năng của vật.
- Bài 3: Một ô tô có khối lượng 1000 kg đang chuyển động với vận tốc 20 m/s. Tính công cần thiết để tăng vận tốc của ô tô lên 30 m/s.
2. Bài tập nâng cao
- Bài 4: Một vật có khối lượng 4 kg đang chuyển động với vận tốc 3 m/s thì đập vào một vật khác có khối lượng 6 kg đang đứng yên. Sau va chạm, hai vật dính vào nhau và cùng chuyển động. Tính động năng của hệ trước và sau va chạm.
- Bài 5: Một viên đạn khối lượng 10g được bắn ra từ một khẩu súng có khối lượng 5kg. Biết vận tốc của viên đạn ngay sau khi rời khỏi nòng súng là 400 m/s. Tính độ biến thiên động năng của khẩu súng và viên đạn.
3. Bài tập ứng dụng thực tế
- Bài 6: Một tàu lượn siêu tốc bắt đầu di chuyển từ đỉnh dốc với vận tốc 0 m/s và trượt xuống dưới dốc không ma sát. Tính độ biến thiên động năng của tàu khi nó đạt vận tốc 25 m/s tại chân dốc.
- Bài 7: Một vật nặng được thả rơi tự do từ độ cao 20m. Tính độ biến thiên động năng của vật khi chạm đất. Bỏ qua lực cản của không khí.
Những bài tập trên đây giúp các bạn hiểu sâu hơn về mối quan hệ giữa công và độ biến thiên động năng, từ đó có thể áp dụng vào các tình huống thực tế khác nhau.
VI. Tổng Kết Và Kết Luận
Độ biến thiên động năng là một khái niệm quan trọng trong vật lý học, không chỉ giúp chúng ta hiểu rõ hơn về sự chuyển động của vật thể mà còn có ứng dụng thực tiễn trong nhiều lĩnh vực khác nhau. Qua các phần kiến thức đã trình bày, chúng ta đã nắm vững được khái niệm, mối quan hệ giữa công và độ biến thiên động năng, các yếu tố ảnh hưởng đến động năng, cũng như những ứng dụng thực tiễn quan trọng.
1. Tóm tắt kiến thức quan trọng
- Động năng là năng lượng mà một vật có được do sự chuyển động của nó. Công thức tính động năng là \( W_{đ} = \frac{1}{2}mv^2 \), trong đó \( m \) là khối lượng và \( v \) là vận tốc của vật.
- Độ biến thiên động năng phản ánh sự thay đổi của động năng khi có tác dụng của các lực lên vật. Định lý công - độ biến thiên động năng cho thấy công của các lực tác dụng bằng với độ biến thiên động năng của vật.
- Các yếu tố như khối lượng, vận tốc, và lực tác dụng đều ảnh hưởng trực tiếp đến độ biến thiên động năng của vật.
2. Đánh giá và nhận xét
Việc hiểu rõ độ biến thiên động năng không chỉ giúp chúng ta giải quyết các bài toán cơ học một cách chính xác, mà còn cung cấp cơ sở lý thuyết để phát triển các ứng dụng trong đời sống và công nghiệp. Từ việc thiết kế các hệ thống động lực, các thiết bị an toàn cho đến ứng dụng trong kỹ thuật, động năng và độ biến thiên động năng đóng vai trò then chốt.
3. Hướng dẫn nghiên cứu thêm
- Nghiên cứu thêm về các trường hợp đặc biệt của độ biến thiên động năng, như trong hệ thống có ma sát hoặc lực không bảo toàn.
- Thực hiện các thí nghiệm thực tế để quan sát và đo lường sự biến thiên động năng trong các tình huống khác nhau.
- Tìm hiểu thêm về các ứng dụng tiên tiến của độ biến thiên động năng trong các lĩnh vực như xe điện, năng lượng tái tạo, và kỹ thuật hàng không.
Như vậy, thông qua việc nắm vững kiến thức về động năng và độ biến thiên động năng, chúng ta không chỉ có thể giải quyết các bài toán trong học tập mà còn mở ra nhiều hướng nghiên cứu và ứng dụng mới trong tương lai.