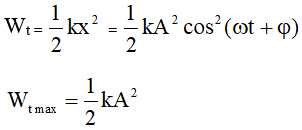Công Thức Tính Động Năng Lớp 12: Hướng Dẫn Đầy Đủ Và Bài Tập Mẫu

Động năng là một dạng năng lượng mà một vật có được do chuyển động của nó. Đối với chương trình Vật lý lớp 12, công thức tính động năng được sử dụng phổ biến trong các bài tập liên quan đến vật lý cơ bản.

1. Công Thức Tính Động Năng

Công thức tính động năng của một vật có khối lượng m và vận tốc v được xác định như sau:

\( W_{đ} = \frac{1}{2} m v^2 \)

• Trong đó:
• \( W_{đ} \): Động năng của vật (đơn vị: Joule, J)
• \( m \): Khối lượng của vật (đơn vị: kg)
• \( v \): Vận tốc của vật (đơn vị: m/s)

2. Định Lý Biến Thiên Động Năng

Định lý này phát biểu rằng độ biến thiên động năng của một vật bằng công của lực tác dụng lên vật đó:

\( \Delta W_{đ} = W_{\text{công}} \)

• \( \Delta W_{đ} \): Độ biến thiên động năng
• \( W_{\text{công}} \): Công thực hiện bởi lực tác dụng

3. Bài Tập Ví Dụ

Dưới đây là một số ví dụ về bài tập liên quan đến động năng:

1. Một ô tô có khối lượng \( m = 1000 \, \text{kg} \) chuyển động với vận tốc \( v = 20 \, \text{m/s} \). Tính động năng của ô tô.
2. Một vật có khối lượng \( m = 2 \, \text{kg} \) rơi tự do từ độ cao \( h = 10 \, \text{m} \). Tính động năng của vật ngay trước khi chạm đất.

Các bài tập này giúp học sinh nắm vững lý thuyết và cách áp dụng công thức tính động năng trong thực tế.

4. Động Năng Của Vật Rắn Quay Quanh Một Trục

Đối với vật rắn quay quanh một trục, động năng được tính bằng:

\( W_{đ} = \frac{1}{2} I \omega^2 \)

• \( I \): Momen quán tính của vật đối với trục quay
• \( \omega \): Vận tốc góc của vật

Hiểu rõ các công thức và cách áp dụng sẽ giúp các em học sinh lớp 12 tự tin hơn trong việc giải quyết các bài tập liên quan đến động năng.

Động năng là một dạng năng lượng mà một vật có được nhờ vào chuyển động của nó. Trong Vật lý, động năng được định nghĩa là công mà lực tác dụng lên vật thực hiện để đưa vật từ trạng thái nghỉ đến trạng thái chuyển động với một vận tốc nhất định.

Động năng được tính toán dựa trên khối lượng và vận tốc của vật, và nó có thể được biểu diễn bằng công thức toán học:

\( W_{đ} = \frac{1}{2} m v^2 \)

• Trong đó:
• \( W_{đ} \): Động năng của vật (đơn vị: Joule, J)
• \( m \): Khối lượng của vật (đơn vị: kilogram, kg)
• \( v \): Vận tốc của vật (đơn vị: meter/second, m/s)

Động năng là một khái niệm cơ bản trong Vật lý, giúp chúng ta hiểu được năng lượng mà vật sở hữu khi chuyển động. Việc nắm vững khái niệm và cách tính động năng là cơ sở để giải quyết nhiều bài toán Vật lý trong chương trình lớp 12.

Động năng là một dạng năng lượng liên quan đến chuyển động của vật. Để tính toán động năng của một vật, chúng ta sử dụng công thức cơ bản sau:

\( W_{đ} = \frac{1}{2} m v^2 \)

• Trong đó:
• \( W_{đ} \): Động năng của vật (đơn vị: Joule, J)
• \( m \): Khối lượng của vật (đơn vị: kilogram, kg)
• \( v \): Vận tốc của vật (đơn vị: meter/second, m/s)

Công thức này cho thấy rằng động năng của một vật tỉ lệ thuận với khối lượng của vật và bình phương vận tốc của nó. Điều này có nghĩa là khi vận tốc của vật tăng gấp đôi, động năng của nó sẽ tăng lên gấp bốn lần, còn nếu khối lượng của vật tăng gấp đôi, động năng cũng sẽ tăng gấp đôi.

Để tính động năng trong các bài toán thực tế, chúng ta cần xác định chính xác khối lượng và vận tốc của vật tại thời điểm xét. Sau đó, áp dụng công thức trên để tính toán giá trị động năng.

Ví dụ: Một chiếc ô tô có khối lượng \( m = 1200 \, kg \) và đang di chuyển với vận tốc \( v = 20 \, m/s \). Động năng của ô tô này sẽ là:

\( W_{đ} = \frac{1}{2} \times 1200 \times 20^2 = 240000 \, J \)

Như vậy, ô tô đang sở hữu một động năng là 240000 Joule. Hiểu và áp dụng chính xác công thức tính động năng sẽ giúp chúng ta giải quyết được nhiều bài toán phức tạp trong Vật lý lớp 12.

Định lý biến thiên động năng là một trong những định lý quan trọng trong cơ học, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa công của lực và sự thay đổi động năng của một vật. Định lý này phát biểu rằng:

Công của tổng các lực tác dụng lên một vật bằng sự biến thiên động năng của vật đó.

Về mặt toán học, định lý được biểu diễn dưới dạng:

\( \Delta W_{đ} = W_{đ2} - W_{đ1} = A \)

• Trong đó:
• \( \Delta W_{đ} \): Độ biến thiên động năng
• \( W_{đ1} \): Động năng ban đầu
• \( W_{đ2} \): Động năng sau cùng
• \( A \): Công của tổng các lực tác dụng lên vật

Theo định lý này, khi lực tác dụng lên một vật và thực hiện công dương, động năng của vật sẽ tăng lên. Ngược lại, nếu công của lực là âm, động năng của vật sẽ giảm đi.

Định lý biến thiên động năng là cơ sở để giải quyết các bài toán liên quan đến công và động năng trong vật lý. Nó cho phép chúng ta dễ dàng tính toán sự thay đổi động năng khi biết công của lực tác dụng, hoặc ngược lại, tính công khi biết sự thay đổi động năng.

Ví dụ: Một vật có khối lượng \( m = 5 \, kg \) chuyển động với vận tốc ban đầu \( v_1 = 2 \, m/s \) và vận tốc sau cùng \( v_2 = 6 \, m/s \). Động năng ban đầu và sau cùng của vật lần lượt là:

• \( W_{đ1} = \frac{1}{2} \times 5 \times 2^2 = 10 \, J \)
• \( W_{đ2} = \frac{1}{2} \times 5 \times 6^2 = 90 \, J \)

Độ biến thiên động năng \( \Delta W_{đ} \) là:

\( \Delta W_{đ} = W_{đ2} - W_{đ1} = 90 - 10 = 80 \, J \)

Như vậy, công của lực tác dụng lên vật là 80 Joule.

Công thức tính động năng có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật. Dưới đây là một số ví dụ tiêu biểu về cách sử dụng công thức này để giải quyết các vấn đề trong thực tế:

• Tính toán động năng của phương tiện giao thông: Động năng của một xe ô tô đang chạy có thể được tính để dự đoán khoảng cách dừng xe khi phanh. Công thức này giúp đánh giá mức độ nguy hiểm trong các tình huống khẩn cấp.
• Xác định công suất của máy móc: Trong các thiết bị công nghiệp, công thức động năng giúp xác định lượng năng lượng cần thiết để tăng tốc hoặc giảm tốc máy móc, từ đó tính toán hiệu suất hoạt động của hệ thống.
• Thiết kế các hệ thống an toàn: Trong lĩnh vực xây dựng và kỹ thuật, công thức động năng được dùng để tính toán khả năng hấp thụ va chạm của các vật liệu như bê tông, thép, nhằm đảm bảo an toàn cho các công trình.
• Ứng dụng trong thể thao: Động năng của các vận động viên khi chạy, nhảy hay ném bóng có thể được tính toán để tối ưu hóa kỹ thuật và hiệu suất thi đấu.

Một ví dụ cụ thể: Một xe ô tô có khối lượng \( m = 1000 \, kg \) đang di chuyển với vận tốc \( v = 20 \, m/s \). Động năng của xe được tính như sau:

\( W_{đ} = \frac{1}{2} \times m \times v^2 = \frac{1}{2} \times 1000 \times 20^2 = 200,000 \, J \)

Như vậy, xe ô tô đang có động năng là 200,000 Joule. Điều này cho thấy xe có một lượng năng lượng lớn mà nếu cần dừng xe gấp, hệ thống phanh phải đủ mạnh để tiêu tán năng lượng này trong khoảng cách ngắn nhất.

Dưới đây là một số bài tập mẫu về động năng, kèm theo lời giải chi tiết. Các bài tập này giúp học sinh lớp 12 hiểu rõ hơn về cách áp dụng công thức tính động năng trong các tình huống thực tế.

• Bài tập 1: Một vật có khối lượng \( m = 2 \, kg \) chuyển động với vận tốc \( v = 3 \, m/s \). Tính động năng của vật.
• Lời giải:

  Động năng của vật được tính bằng công thức:

  \( W_{đ} = \frac{1}{2} \times m \times v^2 \)

  Thay số vào công thức:

  \( W_{đ} = \frac{1}{2} \times 2 \times 3^2 = 9 \, J \)

  Vậy động năng của vật là 9 Joule.

• Bài tập 2: Một xe tải có khối lượng \( m = 1500 \, kg \) đang di chuyển với vận tốc \( v = 15 \, m/s \). Tính động năng của xe tải.
• Lời giải:

  Động năng của xe tải được tính bằng công thức:

  \( W_{đ} = \frac{1}{2} \times m \times v^2 \)

  Thay số vào công thức:

  \( W_{đ} = \frac{1}{2} \times 1500 \times 15^2 = 168,750 \, J \)

  Vậy động năng của xe tải là 168,750 Joule.

• Bài tập 3: Một viên đạn có khối lượng \( m = 50 \, g \) được bắn ra với vận tốc \( v = 800 \, m/s \). Tính động năng của viên đạn.
• Lời giải:

  Động năng của viên đạn được tính bằng công thức:

  \( W_{đ} = \frac{1}{2} \times m \times v^2 \)

  Chuyển đổi khối lượng viên đạn sang đơn vị kg: \( m = 0.05 \, kg \).

  Thay số vào công thức:

  \( W_{đ} = \frac{1}{2} \times 0.05 \times 800^2 = 16,000 \, J \)

  Vậy động năng của viên đạn là 16,000 Joule.

Trong vật lý, động năng và thế năng là hai dạng năng lượng quan trọng thường xuất hiện trong các hệ cơ học. Mối quan hệ giữa động năng và thế năng thể hiện qua định luật bảo toàn cơ năng, một trong những định luật cơ bản của vật lý.

• Động năng là năng lượng mà một vật sở hữu nhờ vào chuyển động của nó. Công thức tính động năng được biểu diễn như sau:

  \( W_{đ} = \frac{1}{2} \times m \times v^2 \)

  trong đó:

  • \( m \) là khối lượng của vật (kg)
  • \( v \) là vận tốc của vật (m/s)
• Thế năng là năng lượng mà một vật sở hữu do vị trí của nó trong một trường lực, chẳng hạn như trường trọng lực hoặc trường lực đàn hồi. Công thức tính thế năng trọng trường là:

  \( W_t = m \times g \times h \)

  trong đó:

  • \( m \) là khối lượng của vật (kg)
  • \( g \) là gia tốc trọng trường (m/s²)
  • \( h \) là độ cao của vật so với mốc chọn (m)
• Mối quan hệ giữa động năng và thế năng:

  Theo định luật bảo toàn cơ năng, tổng động năng và thế năng của một hệ kín luôn không đổi, nếu chỉ có lực bảo toàn tác dụng lên hệ. Cụ thể:

  \( W_{đ} + W_t = \text{const} \)

  Điều này có nghĩa là khi động năng của vật tăng lên, thì thế năng của nó sẽ giảm đi và ngược lại, sao cho tổng cơ năng của hệ là không đổi.