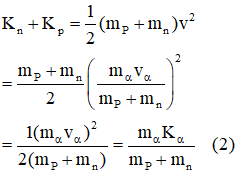Chủ đề động năng con lắc lò xo: Khám phá chi tiết về động năng con lắc lò xo qua bài viết này, từ công thức tính toán đến những ứng dụng thực tế đáng chú ý. Tìm hiểu cách thức động năng thay đổi trong quá trình dao động và cách áp dụng nó trong đời sống hàng ngày cũng như trong kỹ thuật.
Mục lục
Động Năng Của Con Lắc Lò Xo
Con lắc lò xo là một trong những hệ thống dao động điều hòa cơ bản, thường được nghiên cứu trong vật lý. Nó bao gồm một lò xo có độ cứng k và một vật nhỏ có khối lượng m gắn vào đầu lò xo. Khi con lắc dao động, nó sẽ có cả động năng và thế năng, và sự biến đổi giữa hai dạng năng lượng này diễn ra theo quy luật điều hòa.
Động Năng Của Con Lắc Lò Xo
Động năng của con lắc lò xo là năng lượng do chuyển động của vật nặng m tạo ra. Nó được tính bằng công thức:
\(W_{\text{k}} = \frac{1}{2}mv^2\)
Trong đó:
- \(m\): khối lượng của vật (kg)
- \(v\): vận tốc của vật tại thời điểm đang xét (m/s)
Động năng của con lắc đạt giá trị cực đại khi vật đi qua vị trí cân bằng, nơi vận tốc của nó lớn nhất.
Sự Biến Thiên Của Động Năng Và Thế Năng
Trong quá trình dao động, động năng và thế năng của con lắc lò xo liên tục biến đổi qua lại lẫn nhau. Khi động năng tăng thì thế năng giảm và ngược lại, tuy nhiên tổng cơ năng của hệ (tổng của động năng và thế năng) luôn được bảo toàn (khi không có ma sát).
Biểu thức cho sự biến thiên của thế năng trong con lắc lò xo là:
\(W_{\text{t}} = \frac{1}{2}kx^2\)
Trong đó:
- \(k\): độ cứng của lò xo (N/m)
- \(x\): li độ của vật tại thời điểm đang xét (m)
Các Bài Tập Thường Gặp
Dưới đây là một số dạng bài tập liên quan đến động năng của con lắc lò xo:
- Tính động năng tại một vị trí bất kỳ của vật trong quá trình dao động.
- Xác định vận tốc của vật khi biết động năng tại một vị trí cụ thể.
- So sánh động năng và thế năng tại các vị trí khác nhau trong quá trình dao động.
Ứng Dụng Thực Tế
Con lắc lò xo không chỉ là một mô hình lý tưởng trong vật lý mà còn có nhiều ứng dụng trong thực tế, như trong các hệ thống treo của xe cộ, các thiết bị giảm chấn, và nhiều hệ thống cơ học khác cần đến sự dao động điều hòa.
Qua những kiến thức trên, hy vọng các bạn đã nắm vững được cách tính toán và ứng dụng động năng của con lắc lò xo trong các bài tập và tình huống thực tế.
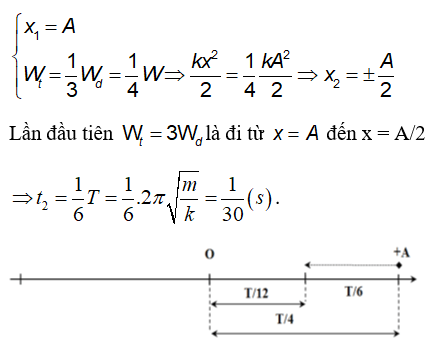
.png)
1. Giới thiệu về con lắc lò xo
Con lắc lò xo là một hệ thống dao động cơ học quan trọng trong vật lý, được sử dụng để nghiên cứu về dao động điều hòa. Nó bao gồm một lò xo có độ cứng nhất định và một vật nặng gắn vào đầu lò xo. Khi lò xo bị kéo giãn hoặc nén, lực đàn hồi sẽ xuất hiện và kéo vật trở về vị trí cân bằng, tạo nên dao động điều hòa.
Các thành phần cơ bản của một con lắc lò xo gồm:
- Vật nặng: Đây là vật có khối lượng \(m\), gắn vào đầu lò xo, có thể dao động qua lại.
- Lò xo: Một vật đàn hồi với độ cứng \(k\), xác định bằng lực cần thiết để kéo giãn hoặc nén lò xo một đơn vị chiều dài.
- Vị trí cân bằng: Vị trí mà lò xo không bị biến dạng, lực tác dụng lên vật bằng 0, vật không chuyển động.
Khi vật dao động, lò xo bị biến dạng và tạo ra một lực đàn hồi kéo vật trở lại vị trí cân bằng. Lực này gây ra sự dao động điều hòa, và năng lượng của hệ thống được phân chia thành động năng và thế năng.
Con lắc lò xo là một mô hình lý tưởng, không chỉ giúp hiểu rõ hơn về các quy luật cơ bản của dao động mà còn có nhiều ứng dụng trong kỹ thuật, từ hệ thống treo xe đến các thiết bị hấp thụ năng lượng.
2. Động năng của con lắc lò xo
Động năng của con lắc lò xo là năng lượng mà vật có được do chuyển động. Động năng này phụ thuộc vào khối lượng của vật và vận tốc của nó. Động năng \(W_k\) được tính theo công thức:
\(W_k = \frac{1}{2}mv^2\)
Trong đó:
- \(m\): khối lượng của vật (kg)
- \(v\): vận tốc của vật tại thời điểm xét (m/s)
Khi vật dao động qua lại quanh vị trí cân bằng, động năng của nó liên tục thay đổi. Tại vị trí biên (xa nhất so với vị trí cân bằng), vận tốc của vật bằng 0, do đó động năng bằng 0. Ngược lại, khi vật đi qua vị trí cân bằng, vận tốc đạt giá trị cực đại, và động năng của nó cũng đạt giá trị lớn nhất.
Ta có thể thấy rằng động năng của con lắc lò xo phụ thuộc trực tiếp vào vận tốc. Để xác định vận tốc của vật tại một vị trí bất kỳ, ta có thể sử dụng định luật bảo toàn năng lượng, cụ thể là sự chuyển đổi giữa động năng và thế năng trong hệ thống.
Biểu thức tổng quát cho động năng của con lắc lò xo tại một vị trí \(x\) bất kỳ (so với vị trí cân bằng) là:
\(W_k = \frac{1}{2}k(A^2 - x^2)\)
Trong đó:
- \(k\): độ cứng của lò xo (N/m)
- \(A\): biên độ dao động (m)
- \(x\): li độ tại vị trí đang xét (m)
Biểu thức này cho thấy rằng động năng phụ thuộc vào cả biên độ và vị trí của vật trong quá trình dao động. Ở vị trí biên, \(x = A\), động năng bằng 0; ở vị trí cân bằng, \(x = 0\), động năng đạt cực đại là \( \frac{1}{2}kA^2 \).
Như vậy, động năng của con lắc lò xo là một phần không thể thiếu trong việc hiểu rõ về dao động điều hòa. Việc nắm vững cách tính và sự biến thiên của động năng giúp chúng ta hiểu sâu hơn về các hiện tượng vật lý liên quan.

3. Thế năng và cơ năng trong con lắc lò xo
Trong con lắc lò xo, ngoài động năng, còn tồn tại thế năng đàn hồi và cơ năng tổng cộng của hệ. Những khái niệm này rất quan trọng trong việc hiểu rõ hơn về dao động điều hòa và các tính chất của nó.
3.1 Thế năng đàn hồi của lò xo
Thế năng đàn hồi là năng lượng dự trữ trong lò xo khi nó bị nén hoặc kéo giãn. Thế năng đàn hồi \(W_t\) được tính bằng công thức:
\(W_t = \frac{1}{2}kx^2\)
Trong đó:
- \(k\): độ cứng của lò xo (N/m)
- \(x\): độ biến dạng của lò xo so với vị trí cân bằng (m)
Khi lò xo bị nén hoặc kéo giãn, thế năng tăng lên, và ngược lại, khi lò xo trở về vị trí cân bằng, thế năng giảm về 0.
3.2 Cơ năng tổng cộng của hệ
Cơ năng của con lắc lò xo là tổng của động năng và thế năng tại mỗi thời điểm trong quá trình dao động. Cơ năng này được bảo toàn trong hệ thống lý tưởng (không có ma sát hay lực cản). Công thức cơ năng tổng cộng \(W\) là:
\(W = W_k + W_t\)
Do cơ năng được bảo toàn, ta có thể biểu diễn nó dưới dạng:
\(W = \frac{1}{2}kA^2\)
Trong đó \(A\) là biên độ dao động. Giá trị này là hằng số trong suốt quá trình dao động.
3.3 Sự chuyển đổi giữa động năng và thế năng
Trong quá trình dao động của con lắc lò xo, động năng và thế năng liên tục chuyển đổi qua lại. Khi vật di chuyển từ vị trí biên về vị trí cân bằng, thế năng giảm và động năng tăng lên. Ngược lại, khi vật di chuyển từ vị trí cân bằng ra vị trí biên, động năng giảm và thế năng tăng lên.
Biểu đồ thể hiện sự thay đổi của động năng và thế năng theo thời gian sẽ cho thấy chúng dao động theo quy luật hình sin, với tần số dao động bằng tần số của con lắc lò xo.
Hiểu rõ về thế năng và cơ năng trong con lắc lò xo không chỉ giúp nắm vững lý thuyết dao động điều hòa mà còn có thể ứng dụng trong các bài toán cơ học phức tạp hơn.

XEM THÊM:
4. Bài tập vận dụng về động năng con lắc lò xo
Để hiểu rõ hơn về động năng của con lắc lò xo, dưới đây là một số bài tập vận dụng từ cơ bản đến nâng cao. Những bài tập này giúp củng cố kiến thức và ứng dụng vào việc giải các bài toán thực tế liên quan đến dao động điều hòa.
4.1 Bài tập cơ bản
-
Một con lắc lò xo có khối lượng \(m = 0,5 \, \text{kg}\) và độ cứng lò xo \(k = 200 \, \text{N/m}\). Hãy tính động năng của con lắc khi vật đi qua vị trí có li độ \(x = 0,1 \, \text{m}\) với biên độ dao động \(A = 0,2 \, \text{m}\).
Lời giải:
Áp dụng công thức động năng:
\(W_k = \frac{1}{2}k(A^2 - x^2)\)
Thay số vào ta có:
\(W_k = \frac{1}{2} \times 200 \times (0,2^2 - 0,1^2) = 3,0 \, \text{J}\)
-
Một vật có khối lượng \(m = 1 \, \text{kg}\) được gắn vào lò xo có độ cứng \(k = 100 \, \text{N/m}\), dao động với biên độ \(A = 0,1 \, \text{m}\). Tính vận tốc của vật khi đi qua vị trí cân bằng.
Lời giải:
Tại vị trí cân bằng, toàn bộ cơ năng chuyển thành động năng:
\(W = \frac{1}{2}kA^2\)
Do đó, vận tốc \(v\) được tính bằng:
\(v = \sqrt{\frac{k}{m}} \times A = \sqrt{\frac{100}{1}} \times 0,1 = 1 \, \text{m/s}\)
4.2 Bài tập nâng cao
-
Một con lắc lò xo dao động với tần số \(f = 2 \, \text{Hz}\) và biên độ \(A = 0,3 \, \text{m}\). Hãy tính động năng cực đại của vật khi biết khối lượng của vật là \(m = 0,2 \, \text{kg}\).
Lời giải:
Động năng cực đại tại vị trí cân bằng được tính bằng:
\(W_{k \, \text{max}} = \frac{1}{2}kA^2\)
Với \(k = 4\pi^2mf^2\), thay số vào ta có:
\(W_{k \, \text{max}} = \frac{1}{2} \times 4\pi^2 \times 0,2 \times 2^2 \times 0,3^2 \approx 7,1 \, \text{J}\)
-
Một con lắc lò xo dao động với biên độ \(A = 0,4 \, \text{m}\) và chu kỳ \(T = 1,5 \, \text{s}\). Hãy tính thế năng và động năng của con lắc tại vị trí cách điểm cân bằng \(x = 0,2 \, \text{m}\).
Lời giải:
Thế năng tại vị trí \(x\) là:
\(W_t = \frac{1}{2}kx^2 = \frac{1}{2} \times \frac{4\pi^2m}{T^2} \times 0,2^2\)
Động năng tại vị trí \(x\) là:
\(W_k = \frac{1}{2}k(A^2 - x^2)\)
4.3 Phân tích đồ thị động năng
Trong phần này, ta sẽ phân tích đồ thị của động năng theo thời gian hoặc theo vị trí của vật trong quá trình dao động. Đồ thị động năng thường có dạng parabol hoặc hình sin, tùy thuộc vào biến số được chọn làm trục hoành. Việc hiểu và phân tích đồ thị này giúp nắm vững mối quan hệ giữa động năng, thế năng, và cơ năng trong dao động điều hòa.

5. Ứng dụng thực tế của con lắc lò xo
Con lắc lò xo không chỉ là một khái niệm quan trọng trong vật lý lý thuyết mà còn có rất nhiều ứng dụng thực tế trong đời sống và công nghệ. Dưới đây là một số ứng dụng tiêu biểu của con lắc lò xo:
5.1 Đồng hồ quả lắc
Đồng hồ quả lắc sử dụng nguyên lý dao động điều hòa của con lắc lò xo để đo thời gian. Chuyển động lặp lại của quả lắc đảm bảo độ chính xác cao trong việc đếm thời gian, và là một ứng dụng tiêu biểu của con lắc trong công nghệ.
5.2 Hệ thống treo trong ô tô
Hệ thống treo của ô tô sử dụng các lò xo để hấp thụ chấn động khi xe di chuyển qua các địa hình không bằng phẳng. Các lò xo trong hệ thống treo hoạt động tương tự như con lắc lò xo, giúp xe di chuyển êm ái và tăng cường độ bám đường.
5.3 Kiểm tra độ cứng của vật liệu
Trong kỹ thuật, con lắc lò xo được sử dụng để kiểm tra độ cứng của các vật liệu khác nhau. Bằng cách quan sát dao động của con lắc khi gắn với vật liệu cần kiểm tra, người ta có thể xác định được độ cứng của vật liệu đó.
5.4 Thiết bị tập thể dục
Các thiết bị tập thể dục như máy chạy bộ và máy kéo tạ thường sử dụng lò xo để tạo ra lực cản. Con lắc lò xo trong những thiết bị này giúp tăng hiệu quả tập luyện và mô phỏng các động tác tự nhiên của cơ thể.
5.5 Ứng dụng trong kỹ thuật và cơ khí
Trong kỹ thuật và cơ khí, con lắc lò xo được sử dụng trong các hệ thống điều khiển dao động, hệ thống giảm chấn, và các cơ chế tự động khác. Những ứng dụng này giúp tối ưu hóa hoạt động của các thiết bị và đảm bảo độ bền lâu dài.
Như vậy, con lắc lò xo không chỉ là một công cụ học tập quan trọng trong vật lý mà còn đóng vai trò không thể thiếu trong nhiều lĩnh vực thực tế, từ đời sống hàng ngày đến các ngành công nghiệp kỹ thuật cao.
6. Kết luận
Qua các nội dung đã được trình bày, chúng ta có thể thấy rằng con lắc lò xo là một hệ cơ học đơn giản nhưng chứa đựng nhiều yếu tố vật lý quan trọng. Việc nắm vững các khái niệm về động năng, thế năng và cơ năng của con lắc lò xo không chỉ giúp chúng ta hiểu rõ hơn về lý thuyết cơ bản mà còn có thể ứng dụng trong nhiều lĩnh vực thực tiễn.
6.1 Tầm quan trọng của việc hiểu về động năng
Hiểu rõ động năng của con lắc lò xo giúp chúng ta có thể phân tích được sự chuyển động của vật trong các hệ cơ học có tính chất tương tự. Động năng không chỉ là một khái niệm lý thuyết mà còn đóng vai trò quan trọng trong việc thiết kế và cải tiến các hệ thống cơ khí, ví dụ như hệ thống treo xe, các thiết bị giảm chấn và nhiều ứng dụng khác.
6.2 Hướng dẫn học tập và ôn luyện
Để nắm vững kiến thức về động năng của con lắc lò xo, các bạn cần:
- Ôn lại lý thuyết: Nắm rõ các khái niệm cơ bản về động năng, thế năng và cách chúng tương tác trong hệ con lắc lò xo.
- Luyện tập bài tập: Thực hiện các bài tập từ cơ bản đến nâng cao để củng cố kiến thức, đặc biệt chú trọng vào phân tích sự thay đổi động năng theo vị trí.
- Phân tích đồ thị: Sử dụng đồ thị động năng để hiểu rõ hơn về cách năng lượng thay đổi trong hệ thống con lắc lò xo.
- Áp dụng thực tế: Thực hiện các thí nghiệm nhỏ hoặc tìm hiểu về các ứng dụng thực tế của con lắc lò xo trong đời sống và công nghiệp.
Với việc kiên trì học tập và thực hành, các bạn sẽ không chỉ hiểu sâu về động năng của con lắc lò xo mà còn có thể vận dụng kiến thức này vào các bài toán và tình huống thực tế một cách hiệu quả.