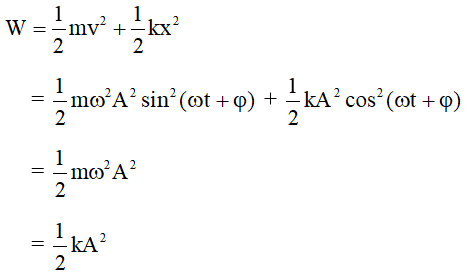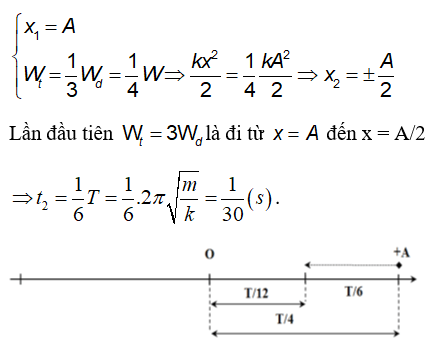Chủ đề chứng minh công thức thế năng hấp dẫn: Chứng minh công thức thế năng hấp dẫn là một chủ đề quan trọng trong vật lý, giúp hiểu rõ hơn về cách lực hấp dẫn hoạt động giữa các vật thể. Bài viết này sẽ cung cấp hướng dẫn chi tiết và phân tích sâu về công thức này, cùng với những ứng dụng thực tiễn giúp người đọc áp dụng kiến thức vào đời sống và nghiên cứu khoa học.
Mục lục
Chứng Minh Công Thức Thế Năng Hấp Dẫn
Thế năng hấp dẫn là một khái niệm quan trọng trong vật lý, đặc biệt trong cơ học cổ điển, khi nghiên cứu về lực hấp dẫn giữa hai vật thể. Công thức thế năng hấp dẫn được dùng để xác định năng lượng tiềm tàng do lực hấp dẫn tạo ra giữa hai vật có khối lượng.
Công Thức Thế Năng Hấp Dẫn
Công thức thế năng hấp dẫn giữa hai vật có khối lượng m1 và m2 cách nhau một khoảng cách r được biểu diễn như sau:
\[ U = -\frac{G \cdot m_1 \cdot m_2}{r} \]
- U: Thế năng hấp dẫn (Joule, J)
- G: Hằng số hấp dẫn (G ≈ 6.674 × 10-11 N(m/kg)2)
- m1, m2: Khối lượng của hai vật (kg)
- r: Khoảng cách giữa hai vật (m)
Chứng Minh Công Thức Thế Năng Hấp Dẫn
Để chứng minh công thức này, ta bắt đầu từ định nghĩa công của lực. Lực hấp dẫn giữa hai vật được biểu diễn bằng công thức:
\[ F = \frac{G \cdot m_1 \cdot m_2}{r^2} \]
Thế năng được định nghĩa là công cần thiết để di chuyển một vật từ vị trí vô cùng xa đến vị trí hiện tại trong trường hấp dẫn. Do đó:
\[ U = - \int_{r}^{\infty} F \cdot dr \]
Thay thế giá trị của lực hấp dẫn F vào:
\[ U = - \int_{r}^{\infty} \frac{G \cdot m_1 \cdot m_2}{r^2} \cdot dr \]
Tiến hành tích phân:
\[ U = - G \cdot m_1 \cdot m_2 \cdot \int_{r}^{\infty} \frac{1}{r^2} \cdot dr \]
Kết quả của tích phân:
\[ U = - G \cdot m_1 \cdot m_2 \left[ -\frac{1}{r} \right]_{r}^{\infty} \]
Từ đó, ta có:
\[ U = - \frac{G \cdot m_1 \cdot m_2}{r} \]
Ý Nghĩa Của Thế Năng Hấp Dẫn
Thế năng hấp dẫn là một dạng năng lượng tiềm tàng thể hiện khả năng thực hiện công việc khi có sự dịch chuyển trong trường hấp dẫn. Nó cho thấy sự tương tác giữa hai vật trong không gian và ảnh hưởng của lực hấp dẫn đến sự dịch chuyển và động năng của các vật thể.
Ứng Dụng Thực Tế
Thế năng hấp dẫn có nhiều ứng dụng trong thực tế, từ việc tính toán quỹ đạo của các hành tinh trong hệ Mặt Trời đến việc dự đoán chuyển động của các vệ tinh nhân tạo quanh Trái Đất. Nó cũng đóng vai trò quan trọng trong việc xác định năng lượng tiềm năng trong các hệ thống thiên văn và cơ học lượng tử.
Trên đây là một cái nhìn tổng quan về công thức và cách chứng minh thế năng hấp dẫn, cũng như ý nghĩa và ứng dụng của nó trong thực tiễn.
.png)
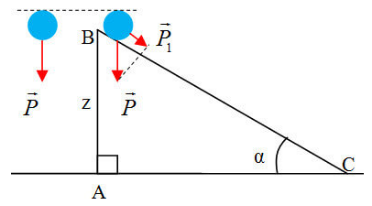
Giới Thiệu Về Thế Năng Hấp Dẫn
Thế năng hấp dẫn là một khái niệm cơ bản trong vật lý, đặc biệt trong lĩnh vực cơ học cổ điển. Nó đề cập đến năng lượng tiềm tàng được lưu trữ trong một hệ thống do lực hấp dẫn giữa các vật thể trong hệ đó. Khái niệm này có tầm quan trọng lớn trong việc giải thích các hiện tượng tự nhiên, từ quỹ đạo của hành tinh trong hệ mặt trời đến các hiện tượng thiên văn quy mô lớn.
Thế năng hấp dẫn có thể hiểu là công cần thiết để di chuyển một vật từ vị trí vô cùng xa về vị trí hiện tại của nó trong trường hấp dẫn của một vật khác. Công thức tính thế năng hấp dẫn giữa hai vật có khối lượng m1 và m2 cách nhau một khoảng cách r được biểu diễn như sau:
\[ U = -\frac{G \cdot m_1 \cdot m_2}{r} \]
- U: Thế năng hấp dẫn (Joule, J)
- G: Hằng số hấp dẫn (G ≈ 6.674 × 10-11 N(m/kg)2)
- m1, m2: Khối lượng của hai vật (kg)
- r: Khoảng cách giữa hai vật (m)
Trong nhiều trường hợp thực tiễn, như tính toán quỹ đạo của các vệ tinh hay dự đoán chuyển động của thiên thể, việc hiểu rõ thế năng hấp dẫn giúp chúng ta giải thích và dự báo chính xác các hiện tượng vật lý trong môi trường có lực hấp dẫn. Hơn nữa, việc nắm vững kiến thức về thế năng hấp dẫn còn mở ra cơ hội để khám phá thêm nhiều hiện tượng thiên nhiên, từ những chuyển động của hành tinh đến các quá trình hình thành sao và thiên hà.
Ứng Dụng Thực Tế Của Thế Năng Hấp Dẫn
Thế năng hấp dẫn, một khái niệm quan trọng trong vật lý, không chỉ tồn tại trong lý thuyết mà còn có rất nhiều ứng dụng thực tế trong cuộc sống và khoa học. Dưới đây là một số ứng dụng tiêu biểu của thế năng hấp dẫn trong các lĩnh vực khác nhau:
- 1. Tính toán quỹ đạo vệ tinh:
Thế năng hấp dẫn được sử dụng để tính toán và dự đoán quỹ đạo của các vệ tinh nhân tạo quay quanh Trái Đất. Việc hiểu rõ về thế năng này giúp các nhà khoa học xác định được vị trí và quỹ đạo ổn định của các vệ tinh, đảm bảo chúng hoạt động hiệu quả cho các mục đích như thông tin liên lạc, quan sát trái đất, và định vị GPS.
- 2. Hệ thống định vị toàn cầu (GPS):
Các hệ thống định vị toàn cầu (GPS) dựa trên nguyên lý thế năng hấp dẫn để xác định vị trí chính xác của các vật thể trên Trái Đất. Thế năng hấp dẫn ảnh hưởng đến chuyển động của các vệ tinh GPS, và việc hiệu chỉnh những ảnh hưởng này là cần thiết để đạt được độ chính xác cao trong định vị.
- 3. Nghiên cứu và khám phá vũ trụ:
Thế năng hấp dẫn là một yếu tố quan trọng trong việc nghiên cứu các hiện tượng thiên văn như chuyển động của các hành tinh, ngôi sao, và thiên hà. Nó giúp các nhà khoa học hiểu rõ hơn về cấu trúc và sự tiến hóa của vũ trụ, cũng như phát hiện các hành tinh ngoài hệ mặt trời và những đối tượng thiên văn khác.
- 4. Thiết kế tàu vũ trụ và tên lửa:
Trong ngành công nghiệp vũ trụ, thế năng hấp dẫn được áp dụng để thiết kế quỹ đạo bay cho các tàu vũ trụ và tên lửa. Điều này giúp tối ưu hóa lượng nhiên liệu tiêu thụ và đảm bảo rằng các nhiệm vụ không gian có thể được thực hiện một cách an toàn và hiệu quả.
- 5. Động lực học chất lỏng và nghiên cứu địa chất:
Thế năng hấp dẫn cũng có ứng dụng trong động lực học chất lỏng, đặc biệt là trong việc nghiên cứu sự di chuyển của nước ngầm và dầu khí. Ngoài ra, nó còn được sử dụng để khảo sát địa chất, giúp phát hiện các mỏ tài nguyên dưới lòng đất thông qua những biến đổi nhỏ trong trường hấp dẫn của Trái Đất.
Như vậy, thế năng hấp dẫn không chỉ là một khái niệm vật lý trừu tượng mà còn có những ứng dụng thực tế, giúp giải quyết nhiều vấn đề trong khoa học và công nghệ, đồng thời mở ra những triển vọng mới trong nghiên cứu và khám phá vũ trụ.