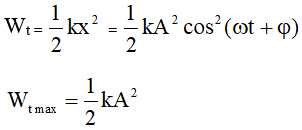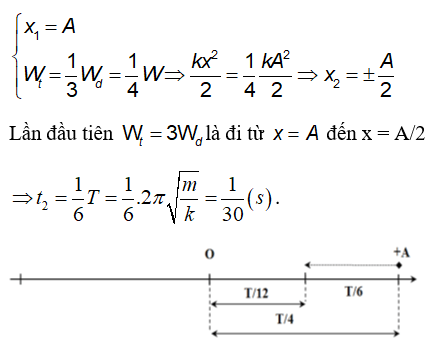Chủ đề thế năng công thức 12: Thế năng công thức 12 là một trong những khái niệm quan trọng trong chương trình Vật lý lớp 12. Bài viết này sẽ giúp bạn nắm vững công thức tính thế năng, hiểu rõ các dạng thế năng, và khám phá ứng dụng thực tế của chúng trong cuộc sống hàng ngày và các lĩnh vực khoa học khác.
Mục lục
Công Thức Tính Thế Năng Lớp 12: Tổng Quan và Ứng Dụng
Thế năng là một khái niệm quan trọng trong vật lý, đặc biệt là trong chương trình học lớp 12. Dưới đây là một cái nhìn tổng quan về các công thức tính thế năng phổ biến và cách chúng được áp dụng trong thực tế.
1. Thế Năng Trọng Trường
Thế năng trọng trường là năng lượng tiềm năng của một vật thể phụ thuộc vào vị trí của nó trong trường hấp dẫn. Công thức tính thế năng trọng trường như sau:
\[
W = m \cdot g \cdot h
\]
- W: Thế năng trọng trường (đơn vị: Joule, J)
- m: Khối lượng của vật (đơn vị: kilogram, kg)
- g: Gia tốc trọng trường (thường lấy giá trị xấp xỉ 9.8 m/s²)
- h: Độ cao của vật so với mốc thế năng (đơn vị: mét, m)
Ví dụ, nếu một vật có khối lượng 2 kg được nâng lên độ cao 5 m, thế năng trọng trường của nó sẽ là:
\[
W = 2 \times 9.8 \times 5 = 98 \, J
\]
2. Thế Năng Đàn Hồi
Thế năng đàn hồi là năng lượng dự trữ trong một vật khi nó bị biến dạng, chẳng hạn như lò xo bị nén hoặc kéo dãn. Công thức tính thế năng đàn hồi:
\[
W_{đh} = \frac{1}{2} k (\Delta l)^2
\]
- Wđh: Thế năng đàn hồi (đơn vị: Joule, J)
- k: Độ cứng của lò xo (đơn vị: Newton trên mét, N/m)
- Δl: Độ biến dạng của lò xo (đơn vị: mét, m)
Ví dụ, một lò xo có độ cứng 150 N/m bị nén 0.1 m, thế năng đàn hồi của lò xo sẽ là:
\[
W_{đh} = \frac{1}{2} \times 150 \times (0.1)^2 = 0.75 \, J
\]
3. Ứng Dụng Thực Tế của Thế Năng
Các công thức tính thế năng không chỉ giới hạn trong lý thuyết mà còn được áp dụng rộng rãi trong nhiều lĩnh vực như:
- Công nghệ: Thiết kế hệ thống lò xo trong xe hơi, cơ chế hoạt động của các thiết bị nâng hạ.
- Kỹ thuật xây dựng: Tính toán tải trọng và các yếu tố an toàn khi xây dựng cầu, nhà cao tầng.
- Khoa học không gian: Xác định năng lượng cần thiết để đưa vệ tinh vào quỹ đạo.
4. Bài Tập Vận Dụng
Dưới đây là một số bài tập mẫu giúp củng cố kiến thức về thế năng:
- Một vật có khối lượng 1 kg được nâng lên độ cao 10 m. Tính thế năng trọng trường của vật.
- Một lò xo có độ cứng 200 N/m bị kéo dãn 5 cm. Tính thế năng đàn hồi của lò xo.
Qua những công thức và ứng dụng thực tế trên, hy vọng các bạn học sinh lớp 12 sẽ nắm vững hơn về thế năng và cách tính toán trong các bài tập vật lý.
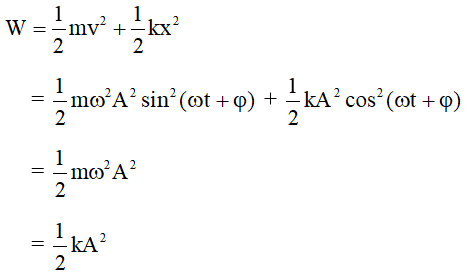
.png)
1. Tổng Quan về Thế Năng
Thế năng là một dạng năng lượng tiềm tàng của một vật, phụ thuộc vào vị trí hoặc trạng thái của nó trong một trường lực nhất định. Trong chương trình Vật lý lớp 12, thế năng thường được chia thành hai loại chính: thế năng trọng trường và thế năng đàn hồi.
- Thế năng trọng trường: Đây là dạng thế năng phổ biến nhất, liên quan đến vị trí của một vật trong trường hấp dẫn của Trái đất. Công thức tính thế năng trọng trường được biểu diễn dưới dạng:
\[ W = m \cdot g \cdot h \]
- W: Thế năng trọng trường (đơn vị: Joule, J)
- m: Khối lượng của vật (đơn vị: kilogram, kg)
- g: Gia tốc trọng trường (thường lấy giá trị xấp xỉ 9.8 m/s²)
- h: Độ cao của vật so với mốc thế năng (đơn vị: mét, m)
- Thế năng đàn hồi: Đây là năng lượng tích trữ trong một vật thể khi nó bị biến dạng, như một lò xo bị nén hoặc kéo dãn. Công thức tính thế năng đàn hồi là:
\[ W_{đh} = \frac{1}{2} k (\Delta l)^2 \]
- Wđh: Thế năng đàn hồi (đơn vị: Joule, J)
- k: Độ cứng của lò xo (đơn vị: Newton trên mét, N/m)
- Δl: Độ biến dạng của lò xo (đơn vị: mét, m)
Thế năng có vai trò quan trọng trong nhiều hiện tượng tự nhiên và ứng dụng kỹ thuật. Ví dụ, trong xây dựng, thế năng trọng trường được tính toán để đảm bảo an toàn cho các công trình cao tầng; trong cơ khí, thế năng đàn hồi của lò xo được ứng dụng trong các thiết bị giảm chấn.
Tóm lại, việc hiểu rõ và nắm vững các công thức tính thế năng giúp học sinh không chỉ giải quyết tốt các bài tập trong sách giáo khoa mà còn ứng dụng được vào các tình huống thực tế khác nhau.
2. Công Thức Tính Thế Năng
Công thức tính thế năng là một phần quan trọng trong chương trình Vật lý lớp 12, giúp học sinh nắm vững kiến thức về năng lượng tiềm năng của các vật thể trong các trường lực khác nhau. Dưới đây là các công thức tính thế năng phổ biến nhất.
2.1 Công Thức Tính Thế Năng Trọng Trường
Thế năng trọng trường là năng lượng tiềm tàng của một vật khi nó nằm trong trường hấp dẫn của Trái Đất. Công thức để tính thế năng trọng trường là:
\[
W = m \cdot g \cdot h
\]
- W: Thế năng trọng trường (đơn vị: Joule, J)
- m: Khối lượng của vật (đơn vị: kilogram, kg)
- g: Gia tốc trọng trường (đơn vị: mét trên giây bình phương, m/s²)
- h: Độ cao của vật so với mốc thế năng (đơn vị: mét, m)
Ví dụ, nếu một vật có khối lượng 2 kg được nâng lên độ cao 10 m so với mặt đất, thế năng trọng trường của nó sẽ là:
\[
W = 2 \times 9.8 \times 10 = 196 \, J
\]
2.2 Công Thức Tính Thế Năng Đàn Hồi
Thế năng đàn hồi là năng lượng tích trữ trong một vật khi nó bị biến dạng, chẳng hạn như một lò xo bị nén hoặc kéo dãn. Công thức để tính thế năng đàn hồi là:
\[
W_{đh} = \frac{1}{2} k (\Delta l)^2
\]
- Wđh: Thế năng đàn hồi (đơn vị: Joule, J)
- k: Độ cứng của lò xo (đơn vị: Newton trên mét, N/m)
- Δl: Độ biến dạng của lò xo (đơn vị: mét, m)
Ví dụ, nếu một lò xo có độ cứng 100 N/m và bị kéo dãn 0.05 m, thế năng đàn hồi của lò xo sẽ được tính như sau:
\[
W_{đh} = \frac{1}{2} \times 100 \times (0.05)^2 = 0.125 \, J
\]
2.3 So Sánh Giữa Thế Năng Trọng Trường và Thế Năng Đàn Hồi
Mặc dù cả hai dạng thế năng đều liên quan đến năng lượng tiềm tàng, thế năng trọng trường phụ thuộc vào vị trí của vật trong trường hấp dẫn, trong khi thế năng đàn hồi phụ thuộc vào độ biến dạng của vật thể. Mỗi loại thế năng có ứng dụng riêng trong thực tế, từ việc tính toán tải trọng trong xây dựng đến thiết kế cơ chế hoạt động của các thiết bị cơ khí.
Việc hiểu rõ và áp dụng đúng các công thức tính thế năng sẽ giúp học sinh giải quyết tốt các bài tập và ứng dụng kiến thức vào thực tế một cách hiệu quả.

3. Ứng Dụng Thế Năng Trong Thực Tế
Thế năng là một khái niệm quan trọng không chỉ trong vật lý lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống và các lĩnh vực khoa học kỹ thuật. Dưới đây là một số ứng dụng tiêu biểu của thế năng trong thực tế.
3.1 Thế Năng Trong Kỹ Thuật Xây Dựng
Trong xây dựng, thế năng trọng trường đóng vai trò quan trọng trong việc tính toán các lực tác động lên các cấu trúc cao tầng như tòa nhà, cầu đường, và các công trình dân dụng khác. Độ cao của các tòa nhà cao tầng tạo ra một lượng lớn thế năng, yêu cầu phải tính toán kỹ lưỡng để đảm bảo an toàn khi có các tác động như gió hoặc động đất.
Ví dụ, khi xây dựng một tòa nhà, thế năng trọng trường của các vật liệu ở các tầng cao cần được cân nhắc để tránh tình trạng mất cân bằng và đảm bảo độ bền vững của công trình.
3.2 Thế Năng Trong Công Nghệ và Cơ Khí
Trong lĩnh vực cơ khí, thế năng đàn hồi là cơ sở để thiết kế các thiết bị giảm chấn, hệ thống treo xe hơi, và các cơ cấu hoạt động dựa trên lò xo. Những hệ thống này sử dụng thế năng đàn hồi để hấp thụ và giải phóng năng lượng khi cần thiết, giúp giảm thiểu các chấn động và tăng cường sự ổn định của các thiết bị.
Ví dụ, hệ thống treo của ô tô sử dụng lò xo để hấp thụ chấn động từ mặt đường, giúp xe di chuyển êm ái hơn. Thế năng đàn hồi trong lò xo chuyển hóa thành động năng để hấp thụ lực tác động và giảm rung lắc.
3.3 Thế Năng Trong Khoa Học Không Gian
Trong lĩnh vực khoa học không gian, thế năng trọng trường là yếu tố quan trọng trong việc phóng và điều khiển quỹ đạo của vệ tinh, tàu vũ trụ. Các kỹ sư phải tính toán chính xác thế năng của các thiết bị này để đảm bảo chúng đạt được tốc độ thoát khỏi lực hấp dẫn của Trái Đất và duy trì quỹ đạo mong muốn.
Ví dụ, khi phóng vệ tinh vào không gian, thế năng trọng trường của vệ tinh ở độ cao nhất định sẽ chuyển hóa thành động năng, giúp vệ tinh duy trì quỹ đạo ổn định quanh Trái Đất.
Như vậy, thế năng không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thiết thực trong đời sống và công nghệ, từ xây dựng, cơ khí đến khoa học không gian.

XEM THÊM:
4. Bài Tập và Ví Dụ Về Thế Năng
Để hiểu rõ hơn về các khái niệm và công thức liên quan đến thế năng, học sinh cần thực hành thông qua các bài tập và ví dụ cụ thể. Dưới đây là một số bài tập điển hình và các bước giải chi tiết.
4.1 Bài Tập Thế Năng Trọng Trường
Bài tập 1: Một vật có khối lượng 5 kg được đặt ở độ cao 20 m so với mặt đất. Tính thế năng trọng trường của vật so với mặt đất.
- Bước 1: Xác định các thông số đã cho trong đề bài.
- Khối lượng vật: \(m = 5 \, kg\)
- Độ cao so với mặt đất: \(h = 20 \, m\)
- Gia tốc trọng trường: \(g = 9.8 \, m/s^2\)
- Bước 2: Sử dụng công thức tính thế năng trọng trường:
\[ W = m \cdot g \cdot h \]
- Bước 3: Thay các giá trị đã biết vào công thức:
\[ W = 5 \times 9.8 \times 20 = 980 \, J \]
Vậy, thế năng trọng trường của vật so với mặt đất là 980 J.
4.2 Bài Tập Thế Năng Đàn Hồi
Bài tập 2: Một lò xo có độ cứng 150 N/m bị nén một đoạn 0.1 m. Tính thế năng đàn hồi của lò xo.
- Bước 1: Xác định các thông số đã cho trong đề bài.
- Độ cứng của lò xo: \(k = 150 \, N/m\)
- Độ biến dạng của lò xo: \(\Delta l = 0.1 \, m\)
- Bước 2: Sử dụng công thức tính thế năng đàn hồi:
\[ W_{đh} = \frac{1}{2} k (\Delta l)^2 \]
- Bước 3: Thay các giá trị đã biết vào công thức:
\[ W_{đh} = \frac{1}{2} \times 150 \times (0.1)^2 = 0.75 \, J \]
Vậy, thế năng đàn hồi của lò xo là 0.75 J.
4.3 Bài Tập Tổng Hợp
Bài tập 3: Một vật có khối lượng 2 kg được treo trên một lò xo có độ cứng 200 N/m. Vật làm lò xo dãn một đoạn 0.05 m so với vị trí cân bằng. Tính tổng thế năng của hệ thống.
- Bước 1: Tính thế năng trọng trường của vật.
- Dùng công thức: \(W_{tt} = m \cdot g \cdot h\)
- Thay số: \(W_{tt} = 2 \times 9.8 \times 0.05 = 0.98 \, J\)
- Bước 2: Tính thế năng đàn hồi của lò xo.
- Dùng công thức: \(W_{đh} = \frac{1}{2} k (\Delta l)^2\)
- Thay số: \(W_{đh} = \frac{1}{2} \times 200 \times (0.05)^2 = 0.25 \, J\)
- Bước 3: Tính tổng thế năng của hệ thống:
- Tổng thế năng: \(W_{tổng} = W_{tt} + W_{đh} = 0.98 + 0.25 = 1.23 \, J\)
Vậy, tổng thế năng của hệ thống là 1.23 J.
Các bài tập trên giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải bài tập liên quan đến thế năng, từ đó có thể áp dụng vào các tình huống thực tế một cách hiệu quả.

5. Các Lưu Ý Khi Học và Ứng Dụng Thế Năng
Trong quá trình học tập và áp dụng kiến thức về thế năng, học sinh cần chú ý một số điểm quan trọng để hiểu rõ hơn và tránh các sai sót phổ biến. Dưới đây là các lưu ý quan trọng cần nhớ khi học và ứng dụng thế năng.
5.1 Hiểu Rõ Khái Niệm Cơ Bản
Thế năng có hai loại chính là thế năng trọng trường và thế năng đàn hồi. Học sinh cần hiểu rõ sự khác biệt giữa hai loại thế năng này, cũng như các điều kiện để áp dụng công thức chính xác. Ví dụ, thế năng trọng trường chỉ liên quan đến độ cao và khối lượng, trong khi thế năng đàn hồi liên quan đến độ cứng của lò xo và độ biến dạng.
5.2 Nhận Biết Đúng Tình Huống Áp Dụng
Trong các bài toán, cần xác định chính xác khi nào cần áp dụng công thức tính thế năng trọng trường hoặc thế năng đàn hồi. Nhiều khi, bài toán có thể yêu cầu tính cả hai loại thế năng, do đó cần phân biệt rõ các yếu tố ảnh hưởng đến từng loại thế năng trong bài toán.
5.3 Đơn Vị Đo Lường và Dấu Kết Quả
Đảm bảo sử dụng đúng đơn vị đo lường trong các phép tính, chẳng hạn như đơn vị của khối lượng là kilogram (kg), của gia tốc trọng trường là mét trên giây bình phương (m/s²), và của thế năng là joule (J). Hơn nữa, học sinh nên chú ý đến dấu của kết quả, đặc biệt là trong các bài toán có liên quan đến độ cao âm (dưới mặt đất).
5.4 Thực Hành Thường Xuyên
Việc giải bài tập thường xuyên là cách tốt nhất để củng cố kiến thức. Học sinh nên tìm các bài tập đa dạng để thực hành, từ những bài đơn giản về tính thế năng trọng trường đến các bài phức tạp kết hợp cả thế năng trọng trường và đàn hồi. Điều này giúp nâng cao kỹ năng giải quyết vấn đề và ứng dụng kiến thức vào thực tiễn.
5.5 Áp Dụng Kiến Thức Vào Thực Tiễn
Thế năng không chỉ tồn tại trong sách vở mà còn có nhiều ứng dụng trong đời sống và kỹ thuật. Học sinh nên tìm hiểu cách mà thế năng được sử dụng trong các ngành công nghiệp như xây dựng, cơ khí, và khoa học không gian, từ đó thấy được tầm quan trọng của việc học và hiểu thế năng.
Bằng cách nắm vững các lưu ý trên, học sinh sẽ dễ dàng hơn trong việc tiếp cận các bài toán về thế năng và có thể áp dụng kiến thức này một cách hiệu quả trong học tập cũng như trong các lĩnh vực thực tế.
6. Tài Liệu Tham Khảo và Đọc Thêm
Để hiểu rõ hơn về thế năng và các ứng dụng của nó trong thực tế, bạn có thể tham khảo các tài liệu sau đây:
- Sách Giáo Khoa Vật Lý 12: Đây là tài liệu cơ bản giúp bạn nắm vững các khái niệm về thế năng, công thức tính toán và các dạng bài tập liên quan. Các chương về thế năng trong sách giáo khoa cung cấp kiến thức nền tảng và các ví dụ minh họa cụ thể.
- Thế Năng và Các Ứng Dụng Thực Tế: Các trang web như cung cấp nhiều bài tập và lời giải chi tiết về thế năng, bao gồm cả các bài tập trắc nghiệm và tự luận. Đây là nguồn tài liệu hữu ích để bạn ôn tập và nâng cao kỹ năng giải bài tập.
- Bài Giảng và Video Hướng Dẫn: Để có cái nhìn trực quan hơn, bạn có thể tìm các video bài giảng trên các nền tảng giáo dục như YouTube hoặc các trang web học tập trực tuyến như . Các video này thường đi kèm với hình ảnh minh họa sinh động và giải thích chi tiết giúp bạn dễ dàng nắm bắt kiến thức hơn.
- Tài Liệu Bổ Trợ về Thế Năng: Trên các blog giáo dục như , bạn có thể tìm thấy các bài viết chuyên sâu về thế năng, bao gồm công thức tính toán, các dạng thế năng, và ứng dụng của chúng trong nhiều lĩnh vực khác nhau như kỹ thuật, khoa học và công nghệ.
Những tài liệu này không chỉ giúp bạn củng cố kiến thức cơ bản mà còn mở rộng hiểu biết về ứng dụng của thế năng trong thực tế, từ đó giúp bạn tự tin hơn khi học tập và làm bài tập liên quan đến chủ đề này.