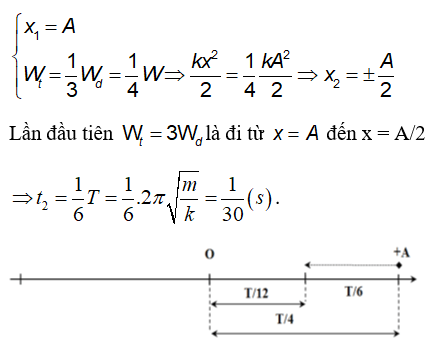Công Thức Tính Thế Năng Đàn Hồi Của Lò Xo: Hướng Dẫn Chi Tiết Và Ứng Dụng Thực Tế

Thế năng đàn hồi là năng lượng mà một hệ vật có được do tác động của lực đàn hồi. Đối với lò xo, thế năng này được lưu trữ khi lò xo bị nén hoặc kéo dãn ra khỏi trạng thái cân bằng.

Công Thức Tính Thế Năng Đàn Hồi

Công thức tổng quát để tính thế năng đàn hồi của lò xo là:

$$ W_t = \frac{1}{2} k x^2 $$

• W_t: Thế năng đàn hồi (Joules)
• k: Độ cứng của lò xo (N/m)
• x: Độ biến dạng của lò xo (m)

Ví Dụ Minh Họa

Giả sử chúng ta có một lò xo với hằng số đàn hồi k = 150 N/m và lò xo bị kéo dãn một đoạn x = 0.2 m. Thế năng đàn hồi được tính như sau:

$$ W_t = \frac{1}{2} \times 150 \times (0.2)^2 = 3 \, J $$

Thế năng đàn hồi của lò xo trong trường hợp này là 3 Joules.

Ứng Dụng Của Thế Năng Đàn Hồi

Thế năng đàn hồi có nhiều ứng dụng thực tiễn trong đời sống và công nghiệp:

• Hệ thống treo ô tô: Sử dụng lò xo để hấp thụ và giải phóng năng lượng khi xe di chuyển qua địa hình không bằng phẳng.
• Dụng cụ thể thao: Cung tên, máy tập thể dục sử dụng thế năng đàn hồi để tạo ra lực và chuyển động.
• Thiết bị gia dụng: Các sản phẩm như bút bi, đồng hồ cơ học sử dụng cơ chế thế năng đàn hồi.

Kết Luận

Việc hiểu và áp dụng công thức tính thế năng đàn hồi không chỉ giúp giải quyết các bài toán vật lý mà còn góp phần cải tiến hiệu suất trong các ứng dụng công nghệ và đời sống hàng ngày.

Thế năng đàn hồi là một dạng năng lượng được lưu trữ trong lò xo khi nó chịu tác dụng của lực đàn hồi. Khi lò xo bị biến dạng (kéo dài hoặc nén lại), lực đàn hồi phát sinh theo định luật Hooke, tỷ lệ thuận với độ biến dạng của lò xo. Công thức tính thế năng đàn hồi của lò xo là:

1. Công thức: $$ W_e = \frac{1}{2} k x^2 $$

2. Trong đó:

   • k: Độ cứng của lò xo (N/m).
   • x: Độ biến dạng của lò xo (m).

Khi lò xo bị biến dạng lớn nhất, thế năng đàn hồi đạt cực đại và ngược lại, khi lò xo không bị biến dạng, thế năng đàn hồi bằng 0. Quá trình biến dạng và phục hồi của lò xo tạo nên dao động điều hòa, chuyển đổi liên tục giữa động năng và thế năng đàn hồi.

Công thức tính thế năng đàn hồi của lò xo dựa trên định luật Hooke, phản ánh mối quan hệ giữa lực đàn hồi và độ biến dạng của lò xo. Cụ thể, khi lò xo bị kéo dài hoặc nén lại, năng lượng tích trữ trong lò xo được gọi là thế năng đàn hồi. Công thức chung để tính thế năng này là:

$$ W_e = \frac{1}{2} k x^2 $$

1. Đại lượng:

   • W_e: Thế năng đàn hồi (Joule).
   • k: Độ cứng của lò xo (N/m).
   • x: Độ biến dạng của lò xo (m).

2. Ý nghĩa: Thế năng đàn hồi là năng lượng mà lò xo có thể giải phóng khi trở lại trạng thái ban đầu. Giá trị này càng lớn khi độ biến dạng hoặc độ cứng của lò xo tăng.

3. Ví dụ tính toán: Xét một lò xo có độ cứng k = 200 N/m và bị kéo dài một đoạn x = 0.05 m. Thế năng đàn hồi của lò xo được tính như sau:

   $$ W_e = \frac{1}{2} \times 200 \times (0.05)^2 = 0.25 \, J $$

Qua ví dụ trên, bạn có thể thấy rằng công thức tính thế năng đàn hồi của lò xo giúp xác định được năng lượng tích trữ khi lò xo bị biến dạng, một kiến thức quan trọng trong vật lý và các ứng dụng thực tiễn.

Thế năng đàn hồi của lò xo có nhiều ứng dụng quan trọng trong đời sống và công nghiệp. Dưới đây là một số ví dụ nổi bật về ứng dụng của thế năng đàn hồi:

• Cơ khí: Thế năng đàn hồi được sử dụng trong các hệ thống treo và giảm chấn của ô tô, giúp hấp thụ và làm giảm rung động, đảm bảo sự ổn định và thoải mái khi lái xe.
• Xây dựng: Trong các hệ thống chống động đất, thế năng đàn hồi của lò xo giúp giảm thiểu tác động của rung chấn lên các công trình.
• Y học: Các thiết bị y tế như máy MRI và X-quang sử dụng nguyên lý này để tạo ra chuyển động chính xác.
• Điện tử: Lò xo được sử dụng trong các cảm biến và mạch điện tử để điều chỉnh lực và cân bằng, nâng cao độ chính xác của thiết bị.

Các ứng dụng này thể hiện vai trò quan trọng của thế năng đàn hồi trong nhiều lĩnh vực khác nhau, từ kỹ thuật đến y học và công nghệ.

Con lắc lò xo là một hệ cơ học đơn giản nhưng có tính ứng dụng cao trong nghiên cứu và giảng dạy vật lý. Thế năng đàn hồi của con lắc lò xo là một phần quan trọng trong quá trình chuyển động của hệ thống này.

Trong con lắc lò xo, thế năng đàn hồi được xác định bởi sự biến dạng của lò xo khi nó bị kéo giãn hoặc nén lại. Thế năng này phụ thuộc vào độ cứng của lò xo (k) và độ biến dạng (x) theo công thức:

$$ W_e = \frac{1}{2} k x^2 $$

Khi con lắc lò xo dao động, năng lượng của hệ thống luân phiên giữa thế năng đàn hồi của lò xo và động năng của khối lượng. Tại vị trí biên, khi tốc độ bằng không, thế năng đàn hồi đạt cực đại và bằng toàn bộ năng lượng của hệ thống.

Quá trình này diễn ra liên tục và tạo ra một dao động điều hòa. Do đó, việc hiểu rõ về thế năng đàn hồi trong con lắc lò xo không chỉ giúp giải thích các hiện tượng vật lý mà còn ứng dụng trong các lĩnh vực kỹ thuật và khoa học khác nhau.

1. Trạng thái cân bằng: Thế năng đàn hồi bằng không khi lò xo ở trạng thái không biến dạng.
2. Trạng thái biên: Khi lò xo đạt độ giãn hoặc nén tối đa, thế năng đàn hồi đạt giá trị lớn nhất.
3. Chuyển động điều hòa: Trong quá trình dao động, thế năng đàn hồi và động năng liên tục chuyển đổi qua lại, duy trì tổng năng lượng của hệ thống.

Qua các khía cạnh trên, thế năng đàn hồi trong con lắc lò xo không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế trong nghiên cứu và phát triển công nghệ.