Chủ đề mốc thế năng là gì: Mốc thế năng là gì? Đây là khái niệm quan trọng trong vật lý, giúp xác định vị trí và giá trị thế năng của một vật trong một hệ quy chiếu. Bài viết này sẽ giúp bạn hiểu rõ hơn về cách chọn mốc thế năng, công thức tính toán liên quan và các ứng dụng thực tiễn trong cuộc sống, từ đó áp dụng vào việc giải bài toán vật lý hiệu quả.
Mục lục
Mốc thế năng là gì?
Trong vật lý học, mốc thế năng là một khái niệm cơ bản, được sử dụng để xác định giá trị của thế năng trong các hệ thống cơ học. Thế năng là năng lượng mà một vật có được do vị trí của nó trong một trường lực, chẳng hạn như trường trọng lực hay trường điện.
Khái niệm mốc thế năng
Mốc thế năng là một vị trí được chọn làm gốc để đo thế năng của một vật. Tại vị trí này, giá trị thế năng được đặt bằng 0. Việc chọn mốc thế năng là tương đối và phụ thuộc vào cách lựa chọn của người tính toán, tuy nhiên cần thống nhất khi áp dụng vào một bài toán cụ thể.
Ví dụ về mốc thế năng
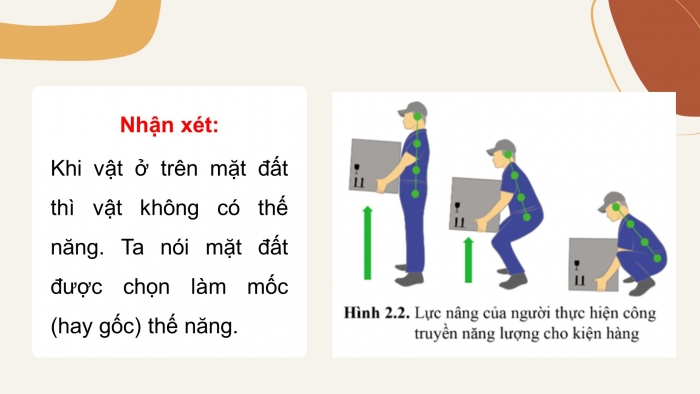
- Khi nghiên cứu chuyển động của một vật trên mặt đất, mốc thế năng thường được chọn là mặt đất.
- Trong các bài toán về chuyển động ném, mốc thế năng có thể được chọn tại vị trí điểm ném ban đầu.
- Trong trường hợp tính toán trong không gian, mốc thế năng có thể được chọn tại một điểm vô cùng xa.
Công thức liên quan
Thế năng hấp dẫn của một vật có khối lượng m tại độ cao h so với mốc thế năng được tính bằng công thức:
\[
W = mgh
\]
Trong đó:
- W là thế năng (đơn vị: Joule)
- m là khối lượng của vật (đơn vị: kg)
- g là gia tốc trọng trường (thường là 9,8 m/s2 trên Trái Đất)
- h là độ cao so với mốc thế năng (đơn vị: mét)
Tầm quan trọng của việc chọn mốc thế năng
Việc chọn mốc thế năng phù hợp giúp đơn giản hóa việc tính toán, tránh nhầm lẫn và tạo thuận lợi cho việc giải các bài toán vật lý phức tạp.
.png)
1. Khái niệm mốc thế năng
Mốc thế năng là một vị trí được chọn làm gốc để xác định giá trị thế năng của một vật trong một hệ quy chiếu. Thế năng phụ thuộc vào vị trí của vật trong trường lực, như trường trọng lực hoặc trường điện.
Thông thường, mốc thế năng được chọn sao cho tại đó giá trị thế năng bằng 0. Việc chọn mốc thế năng là tương đối, tùy thuộc vào mục đích của bài toán và cách tiếp cận của người giải. Điều này có thể thay đổi tùy theo tình huống thực tế.
Trong vật lý, thế năng hấp dẫn của một vật được tính theo công thức:
\[
W = mgh
\]
Trong đó:
- W: Thế năng (đơn vị: Joule)
- m: Khối lượng của vật (đơn vị: kg)
- g: Gia tốc trọng trường (thường là 9,8 m/s2)
- h: Độ cao của vật so với mốc thế năng (đơn vị: mét)
Ví dụ, khi tính thế năng của một vật trên mặt đất, mốc thế năng thường được chọn là mặt đất (h = 0). Tuy nhiên, trong các bài toán khác, mốc thế năng có thể được chọn tại một vị trí khác như điểm ném, hoặc thậm chí tại vô cực.
Việc chọn đúng mốc thế năng không chỉ giúp đơn giản hóa tính toán mà còn đảm bảo kết quả phù hợp với thực tế, nhất là trong các bài toán liên quan đến năng lượng và chuyển động.
2. Cách chọn mốc thế năng
Việc chọn mốc thế năng là một bước quan trọng trong việc tính toán và phân tích các bài toán liên quan đến thế năng trong vật lý. Dưới đây là các nguyên tắc và bước cơ bản để chọn mốc thế năng phù hợp:
2.1. Nguyên tắc chọn mốc thế năng
- Vị trí thuận tiện: Mốc thế năng thường được chọn ở vị trí dễ dàng xác định và thuận tiện cho việc tính toán. Chẳng hạn, mặt đất hoặc vị trí thấp nhất trong hệ quy chiếu là những lựa chọn phổ biến.
- Giá trị thế năng bằng 0: Mốc thế năng được chọn sao cho tại đó, thế năng của vật bằng 0. Điều này giúp đơn giản hóa công thức và phép tính trong các bài toán.
- Tùy vào bài toán cụ thể: Trong một số bài toán, mốc thế năng có thể được chọn linh hoạt, chẳng hạn như điểm bắt đầu của vật trong bài toán ném hoặc điểm xa vô cực trong trường hợp trường lực lớn.
2.2. Các trường hợp cụ thể khi chọn mốc thế năng
- Trong bài toán cơ học: Mốc thế năng thường được chọn tại mặt đất hoặc tại vị trí cân bằng của hệ thống.
- Trong bài toán ném vật: Mốc thế năng có thể được chọn tại điểm ném hoặc điểm thấp nhất trong quỹ đạo chuyển động của vật.
- Trong trường hợp nghiên cứu vũ trụ: Mốc thế năng thường được chọn tại vô cực, nơi lực hấp dẫn bằng 0.
2.3. Ví dụ về cách chọn mốc thế năng
Giả sử bạn đang giải một bài toán tính thế năng của một vật nặng 5kg ở độ cao 10m so với mặt đất. Trong trường hợp này, mốc thế năng được chọn là mặt đất (h = 0). Khi đó, thế năng của vật được tính bằng công thức:
\[
W = mgh = 5 \times 9.8 \times 10 = 490 \text{ Joules}
\]
Chọn đúng mốc thế năng không chỉ giúp bài toán trở nên dễ hiểu hơn mà còn đảm bảo tính chính xác khi áp dụng vào thực tế.

3. Ứng dụng của mốc thế năng trong bài toán vật lý
Mốc thế năng là một yếu tố quan trọng trong các bài toán vật lý liên quan đến năng lượng và chuyển động. Việc lựa chọn mốc thế năng phù hợp không chỉ giúp đơn giản hóa phép tính mà còn cung cấp cái nhìn chính xác hơn về sự chuyển hóa năng lượng trong các hệ cơ học. Dưới đây là một số ứng dụng cụ thể của mốc thế năng trong bài toán vật lý:
3.1. Ứng dụng trong bài toán cơ học
Trong các bài toán cơ học, mốc thế năng thường được chọn tại vị trí thấp nhất của hệ thống, như mặt đất hoặc vị trí cân bằng của vật. Điều này giúp dễ dàng xác định giá trị thế năng và tính toán tổng năng lượng của hệ.
- Ví dụ: Khi tính toán chuyển động của một vật rơi tự do từ độ cao h xuống mặt đất, mốc thế năng được chọn là mặt đất. Thế năng của vật tại độ cao h là \( W = mgh \), và khi vật chạm đất, thế năng trở thành 0, toàn bộ năng lượng được chuyển hóa thành động năng.
3.2. Ứng dụng trong bài toán năng lượng
Mốc thế năng giúp tính toán và phân tích sự chuyển hóa giữa thế năng và động năng trong các hệ cơ học. Điều này đặc biệt quan trọng trong việc bảo toàn năng lượng, một nguyên lý cơ bản trong vật lý.
- Ví dụ: Trong một con lắc đơn, mốc thế năng thường được chọn tại vị trí thấp nhất của con lắc. Khi con lắc đạt đến vị trí này, toàn bộ thế năng đã chuyển hóa thành động năng.
3.3. Ứng dụng trong bài toán chuyển động ném
Trong các bài toán liên quan đến chuyển động ném, như ném thẳng đứng hay ném xiên, mốc thế năng có thể được chọn tại vị trí điểm ném hoặc tại mặt đất. Việc chọn mốc thế năng này giúp dễ dàng tính toán thế năng tại các điểm khác nhau trong quỹ đạo chuyển động của vật.
- Ví dụ: Khi ném một quả bóng lên cao từ mặt đất, mốc thế năng thường được chọn tại mặt đất, giúp tính toán chính xác thế năng ở mọi thời điểm trong quá trình chuyển động.
3.4. Ứng dụng trong bài toán vũ trụ
Trong các bài toán liên quan đến trường hấp dẫn trong không gian, mốc thế năng thường được chọn tại vô cực, nơi lực hấp dẫn bằng 0. Điều này giúp định nghĩa rõ ràng giá trị thế năng của các thiên thể khi ở gần nhau.
- Ví dụ: Trong việc tính toán năng lượng để phóng tàu vũ trụ thoát khỏi lực hấp dẫn của Trái Đất, mốc thế năng thường được chọn tại vô cực, và thế năng ở đó được coi là 0.
Như vậy, việc chọn mốc thế năng phù hợp đóng vai trò quan trọng trong việc giải quyết các bài toán vật lý, giúp tối ưu hóa các phép tính và đưa ra kết quả chính xác hơn.

4. Công thức liên quan đến mốc thế năng
Trong vật lý, các công thức liên quan đến mốc thế năng thường xoay quanh thế năng hấp dẫn của vật trong trường trọng lực. Dưới đây là các công thức cơ bản cần biết khi tính toán liên quan đến mốc thế năng:
4.1. Công thức tính thế năng hấp dẫn
Thế năng hấp dẫn của một vật có khối lượng m tại độ cao h so với mốc thế năng được tính bằng công thức:
\[
W = mgh
\]
Trong đó:
- W: Thế năng (đơn vị: Joule)
- m: Khối lượng của vật (đơn vị: kg)
- g: Gia tốc trọng trường (đơn vị: m/s2, thường là 9.8 m/s2 trên Trái Đất)
- h: Độ cao so với mốc thế năng (đơn vị: mét)
Ví dụ, nếu một vật có khối lượng 2kg được đặt ở độ cao 5m so với mặt đất, mốc thế năng được chọn là mặt đất, thì thế năng của vật là:
\[
W = 2 \times 9.8 \times 5 = 98 \text{ Joules}
\]
4.2. Công thức tính tổng năng lượng của hệ
Trong một hệ cơ học, tổng năng lượng E của hệ là tổng của thế năng W và động năng K:
\[
E = W + K
\]
Trong đó, động năng K được tính theo công thức:
\[
K = \frac{1}{2} mv^2
\]
Việc chọn mốc thế năng phù hợp sẽ giúp xác định giá trị thế năng chính xác, từ đó tính toán tổng năng lượng của hệ một cách dễ dàng và chính xác hơn.
4.3. Mối quan hệ giữa mốc thế năng và động năng
Khi một vật di chuyển trong một trường lực, sự thay đổi thế năng được chuyển hóa thành động năng và ngược lại. Công thức liên quan đến sự chuyển hóa này được biểu diễn qua định luật bảo toàn cơ năng:
\[
W_1 + K_1 = W_2 + K_2
\]
Trong đó:
- W1, W2: Thế năng của vật tại hai vị trí khác nhau
- K1, K2: Động năng của vật tại hai vị trí đó
Định luật này cho thấy, trong quá trình di chuyển của vật, năng lượng được bảo toàn thông qua sự chuyển hóa giữa thế năng và động năng, và việc chọn mốc thế năng chính xác giúp việc tính toán trở nên dễ dàng hơn.

5. Các ví dụ thực tế về mốc thế năng
Trong thực tế, mốc thế năng được áp dụng rộng rãi trong các bài toán và tình huống liên quan đến năng lượng, cơ học và chuyển động. Dưới đây là một số ví dụ cụ thể về cách chọn và sử dụng mốc thế năng trong các tình huống thực tế:
5.1. Ví dụ 1: Vật rơi tự do từ độ cao
Giả sử một quả bóng được thả từ độ cao 10m so với mặt đất. Trong trường hợp này, mốc thế năng thường được chọn là mặt đất (h = 0). Khi quả bóng bắt đầu rơi, thế năng giảm dần và được chuyển hóa thành động năng. Thế năng của quả bóng ở độ cao h được tính bằng công thức:
\[
W = mgh
\]
Khi quả bóng chạm đất, thế năng trở về 0, toàn bộ năng lượng đã chuyển hóa thành động năng.
5.2. Ví dụ 2: Con lắc đơn
Trong một con lắc đơn, mốc thế năng thường được chọn tại vị trí thấp nhất của con lắc (điểm cân bằng). Khi con lắc ở vị trí cao nhất trong quá trình dao động, nó có thế năng lớn nhất. Khi nó di chuyển về vị trí cân bằng, thế năng giảm dần và động năng tăng lên. Sự chuyển hóa này giúp con lắc duy trì chuyển động.
5.3. Ví dụ 3: Ném một vật lên cao
Khi ném một quả bóng thẳng đứng từ mặt đất lên cao, mốc thế năng được chọn tại mặt đất. Lúc này, thế năng tại mặt đất là 0. Khi quả bóng đạt đến độ cao lớn nhất, thế năng đạt giá trị lớn nhất và động năng bằng 0. Trong quá trình rơi xuống, thế năng dần chuyển hóa thành động năng cho đến khi quả bóng chạm đất.
5.4. Ví dụ 4: Hệ thống lò xo
Trong bài toán lò xo nén hoặc dãn, mốc thế năng thường được chọn tại vị trí tự nhiên của lò xo (vị trí không bị nén hoặc dãn). Khi lò xo bị nén hoặc kéo dãn, thế năng đàn hồi tăng lên và có thể được tính bằng công thức:
\[
W = \frac{1}{2} kx^2
\]
Trong đó:
- k: Độ cứng của lò xo
- x: Độ biến dạng của lò xo so với vị trí tự nhiên
5.5. Ví dụ 5: Bài toán vũ trụ
Trong các bài toán về trường hấp dẫn của các hành tinh, mốc thế năng thường được chọn tại vô cực, nơi lực hấp dẫn bằng 0. Ví dụ, khi tính toán năng lượng cần thiết để phóng một vệ tinh thoát khỏi lực hấp dẫn của Trái Đất, mốc thế năng được đặt tại vô cực. Điều này giúp dễ dàng xác định thế năng tại các khoảng cách khác nhau từ Trái Đất đến vệ tinh.
Các ví dụ trên cho thấy tầm quan trọng của việc chọn mốc thế năng đúng cách trong nhiều tình huống khác nhau, giúp quá trình tính toán và phân tích trở nên dễ dàng và chính xác hơn.