Chủ đề bài 29 định luật bảo toàn năng lượng: Bài 29 về Định luật Bảo Toàn Năng Lượng mang đến cho bạn cái nhìn toàn diện về một trong những định luật quan trọng nhất trong vật lý. Hãy cùng tìm hiểu cách năng lượng chuyển hóa, bảo toàn và ứng dụng của nó trong cuộc sống hàng ngày qua những ví dụ sinh động và bài tập thực hành chi tiết.
Mục lục
- Định Luật Bảo Toàn Năng Lượng - Bài 29
- I. Giới Thiệu Chung Về Định Luật Bảo Toàn Năng Lượng
- II. Các Dạng Năng Lượng Liên Quan Đến Định Luật Bảo Toàn Năng Lượng
- III. Biểu Thức Toán Học Của Định Luật Bảo Toàn Năng Lượng
- IV. Ví Dụ Minh Họa Định Luật Bảo Toàn Năng Lượng
- V. Bài Tập Thực Hành Về Định Luật Bảo Toàn Năng Lượng
- VI. Ứng Dụng Thực Tiễn Của Định Luật Bảo Toàn Năng Lượng
- VII. Các Nhà Khoa Học Đóng Góp Vào Định Luật Bảo Toàn Năng Lượng
Định Luật Bảo Toàn Năng Lượng - Bài 29
Bài học về định luật bảo toàn năng lượng thường được giảng dạy trong các lớp học Vật lý, đặc biệt là lớp 9 và lớp 12 tại Việt Nam. Định luật bảo toàn năng lượng là một trong những định luật cơ bản của vật lý học, khẳng định rằng năng lượng không tự nhiên sinh ra hay mất đi mà chỉ chuyển hóa từ dạng này sang dạng khác hoặc từ vật này sang vật khác.
1. Khái Niệm Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng phát biểu rằng:
- Năng lượng của một hệ kín là không đổi theo thời gian.
- Trong các quá trình vật lý, năng lượng có thể chuyển từ dạng này sang dạng khác (ví dụ: từ thế năng sang động năng) hoặc từ vật này sang vật khác nhưng tổng năng lượng của hệ không thay đổi.
2. Biểu Thức Của Định Luật Bảo Toàn Năng Lượng
Biểu thức tổng quát của định luật bảo toàn năng lượng có thể được viết như sau:
$$E_{tổng} = E_{động} + E_{thế} + E_{nhiệt} + \dots = \text{hằng số}$$
Trong đó:
- Etổng: Tổng năng lượng của hệ.
- Eđộng: Động năng.
- Ethế: Thế năng.
- Enhiệt: Nhiệt năng, và các dạng năng lượng khác.
3. Ví Dụ Minh Họa
Một ví dụ điển hình của định luật bảo toàn năng lượng là khi ta thả một hòn bi từ trên cao. Trong quá trình rơi:
- Thế năng ban đầu của hòn bi sẽ giảm dần khi nó rơi xuống.
- Động năng của hòn bi sẽ tăng lên tương ứng với tốc độ rơi.
- Tổng thế năng và động năng của hòn bi tại bất kỳ thời điểm nào trong quá trình rơi vẫn giữ nguyên và bằng với thế năng ban đầu khi hòn bi chưa rơi.
4. Ứng Dụng Của Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng được ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và công nghệ:
- Trong cơ học, để tính toán động năng và thế năng của các vật thể chuyển động.
- Trong nhiệt động học, để giải thích các quá trình nhiệt động và sự chuyển hóa năng lượng.
- Trong điện học, để phân tích hiệu suất của các máy móc và thiết bị điện.
5. Một Số Bài Tập Thực Hành
Để hiểu rõ hơn về định luật bảo toàn năng lượng, học sinh thường được yêu cầu giải các bài tập liên quan. Ví dụ:
| Bài Tập | Đề Bài | Lời Giải |
|---|---|---|
| Bài tập 1 | Một vật có khối lượng 5 kg rơi tự do từ độ cao 10 m. Tính cơ năng của vật. | Sử dụng công thức \( W = W_{đ} + W_{t} = \frac{1}{2}mv^2 + mgh \), cơ năng của vật là 490 J. |
| Bài tập 2 | Một chiếc lò xo có độ cứng 200 N/m, bị nén 0.1 m. Tính năng lượng đàn hồi. | Sử dụng công thức \( E = \frac{1}{2}kx^2 \), năng lượng đàn hồi của lò xo là 1 J. |
.png)
I. Giới Thiệu Chung Về Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản và quan trọng nhất trong vật lý học, đóng vai trò nền tảng trong việc hiểu biết các hiện tượng tự nhiên. Định luật này phát biểu rằng năng lượng không thể tự nhiên sinh ra hoặc mất đi mà chỉ có thể chuyển hóa từ dạng này sang dạng khác hoặc truyền từ vật này sang vật khác.
Cụ thể, trong một hệ kín, tổng năng lượng của hệ là một hằng số. Năng lượng có thể tồn tại dưới nhiều dạng khác nhau như:
- Thế năng: Là năng lượng dự trữ do vị trí của vật trong trường lực, chẳng hạn như năng lượng do độ cao của một vật so với mặt đất.
- Động năng: Là năng lượng do chuyển động của vật, được tính dựa trên khối lượng và vận tốc của vật đó.
- Nhiệt năng: Là năng lượng liên quan đến nhiệt độ của vật, thường được sinh ra do ma sát hoặc các quá trình hóa học.
- Điện năng: Là năng lượng của các hạt mang điện di chuyển trong điện trường.
Định luật bảo toàn năng lượng không chỉ giúp chúng ta hiểu rõ hơn về các quá trình vật lý mà còn có ứng dụng rộng rãi trong các lĩnh vực khác nhau như cơ học, nhiệt động học, điện học, và cả trong đời sống hàng ngày. Ví dụ, khi một chiếc xe chuyển động, động năng của xe sẽ tăng lên trong khi nhiên liệu bị tiêu hao. Tổng năng lượng trước và sau khi tiêu hao nhiên liệu vẫn được bảo toàn nhưng đã chuyển hóa thành động năng và nhiệt năng.
II. Các Dạng Năng Lượng Liên Quan Đến Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng liên quan đến nhiều dạng năng lượng khác nhau. Mỗi dạng năng lượng đều có vai trò quan trọng trong các quá trình tự nhiên và công nghệ, từ chuyển động của vật thể đến các quá trình nhiệt động học và điện học. Dưới đây là một số dạng năng lượng chính:
- 1. Thế Năng
- Thế năng hấp dẫn: Được xác định bởi vị trí của vật trong trường hấp dẫn, ví dụ như năng lượng của một vật được nâng lên một độ cao nhất định so với mặt đất.
- Thế năng đàn hồi: Xuất hiện trong các vật thể đàn hồi như lò xo, khi chúng bị nén hoặc kéo giãn.
- 2. Động Năng
- m: Khối lượng của vật thể (kg).
- v: Vận tốc của vật thể (m/s).
- 3. Nhiệt Năng
- 4. Điện Năng
- 5. Năng Lượng Hóa Học
Thế năng là năng lượng được dự trữ do vị trí hoặc cấu hình của một vật trong trường lực. Thế năng bao gồm:
Động năng là năng lượng của một vật thể do chuyển động của nó. Động năng phụ thuộc vào khối lượng và vận tốc của vật thể và được tính theo công thức:
$$E_{động} = \frac{1}{2}mv^2$$
Trong đó:
Nhiệt năng là năng lượng liên quan đến chuyển động của các hạt trong vật chất. Khi nhiệt độ của một vật tăng, chuyển động của các hạt tăng lên, dẫn đến sự gia tăng nhiệt năng. Nhiệt năng thường xuất hiện trong các quá trình ma sát hoặc phản ứng hóa học.
Điện năng là năng lượng của các hạt mang điện di chuyển trong một mạch điện. Điện năng có vai trò quan trọng trong các thiết bị điện tử và hệ thống năng lượng điện.
Năng lượng hóa học là năng lượng được lưu trữ trong liên kết hóa học giữa các nguyên tử và phân tử. Khi các liên kết này bị phá vỡ hoặc hình thành trong các phản ứng hóa học, năng lượng hóa học có thể được giải phóng hoặc hấp thụ.

III. Biểu Thức Toán Học Của Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng có thể được biểu diễn bằng các biểu thức toán học, giúp chúng ta tính toán và phân tích các quá trình vật lý một cách chính xác. Dưới đây là các biểu thức cơ bản:
- 1. Biểu Thức Tổng Quát
- Etổng: Tổng năng lượng của hệ.
- Eđộng: Động năng.
- Ethế: Thế năng.
- Enhiệt: Nhiệt năng và các dạng năng lượng khác.
- 2. Biểu Thức Cụ Thể Cho Các Dạng Năng Lượng
- Động năng: $$E_{động} = \frac{1}{2}mv^2$$
- Thế năng hấp dẫn: $$E_{thế} = mgh$$
- Nhiệt năng: $$Q = mc\Delta T$$
- 3. Ví Dụ Minh Họa
Biểu thức tổng quát của định luật bảo toàn năng lượng trong một hệ kín được viết như sau:
$$E_{tổng} = E_{động} + E_{thế} + E_{nhiệt} + \dots = \text{hằng số}$$
Trong đó:
Các dạng năng lượng khác nhau có thể được biểu diễn bằng các công thức cụ thể:
Hãy xem xét một ví dụ về việc thả rơi tự do một vật thể từ độ cao h xuống đất. Tại độ cao ban đầu, vật có thế năng là:
$$E_{thế} = mgh$$
Khi vật rơi xuống và đạt đến mặt đất, thế năng chuyển hoàn toàn thành động năng:
$$E_{động} = \frac{1}{2}mv^2$$
Trong suốt quá trình rơi, tổng năng lượng của hệ được bảo toàn:
$$mgh = \frac{1}{2}mv^2$$
Biểu thức này cho thấy rằng năng lượng ban đầu (thế năng) được chuyển hóa hoàn toàn thành động năng khi vật chạm đất.

IV. Ví Dụ Minh Họa Định Luật Bảo Toàn Năng Lượng
Để hiểu rõ hơn về định luật bảo toàn năng lượng, hãy xem xét một số ví dụ minh họa cụ thể dưới đây. Những ví dụ này sẽ giúp bạn thấy rõ cách năng lượng được bảo toàn và chuyển hóa trong các quá trình khác nhau.
- 1. Ví Dụ Chuyển Đổi Thế Năng Thành Động Năng
- 2. Ví Dụ Bảo Toàn Năng Lượng Trong Dao Động Cơ Học
- 3. Ví Dụ Chuyển Đổi Năng Lượng Trong Đời Sống Hàng Ngày
Hãy xét một vật có khối lượng m được thả rơi tự do từ độ cao h so với mặt đất. Ban đầu, vật có thế năng hấp dẫn:
$$E_{thế} = mgh$$
Khi vật rơi xuống, thế năng giảm dần và chuyển hóa thành động năng:
$$E_{động} = \frac{1}{2}mv^2$$
Khi chạm đất, toàn bộ thế năng đã chuyển thành động năng, và tổng năng lượng của hệ vẫn được bảo toàn:
$$mgh = \frac{1}{2}mv^2$$
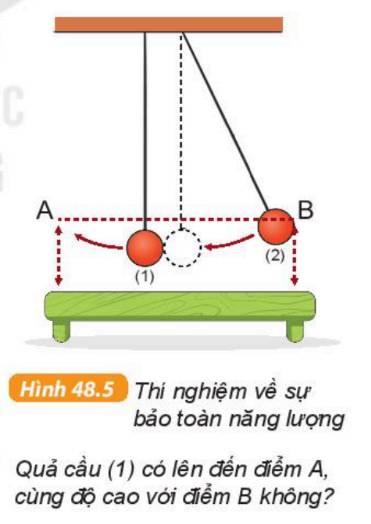
Xét một con lắc đơn dao động không ma sát. Ở vị trí cao nhất, con lắc có thế năng lớn nhất và động năng bằng không:
$$E_{thế} = mgh,\quad E_{động} = 0$$
Khi con lắc di chuyển về vị trí cân bằng, thế năng giảm dần và động năng tăng lên. Tại vị trí cân bằng, động năng đạt giá trị lớn nhất và thế năng bằng không:
$$E_{động} = \frac{1}{2}mv^2,\quad E_{thế} = 0$$
Trong toàn bộ quá trình dao động, tổng năng lượng của con lắc (thế năng + động năng) được bảo toàn:
$$E_{tổng} = E_{thế} + E_{động} = \text{hằng số}$$
Hãy xét một chiếc ô tô đang chuyển động. Động cơ đốt cháy nhiên liệu, chuyển hóa năng lượng hóa học thành cơ năng để đẩy xe đi:
Năng lượng hóa học trong nhiên liệu chuyển hóa thành động năng của ô tô và nhiệt năng do ma sát giữa lốp xe và mặt đường. Tổng năng lượng ban đầu trong nhiên liệu được bảo toàn nhưng đã chuyển đổi sang các dạng năng lượng khác nhau.

V. Bài Tập Thực Hành Về Định Luật Bảo Toàn Năng Lượng
Để củng cố kiến thức về định luật bảo toàn năng lượng, dưới đây là một số bài tập thực hành giúp bạn áp dụng các khái niệm đã học vào thực tế. Hãy giải các bài tập này một cách chi tiết và cẩn thận để hiểu rõ hơn về định luật quan trọng này.
- Bài Tập 1: Rơi Tự Do
- Tính thế năng của vật tại điểm cao nhất.
- Tính động năng của vật ngay trước khi chạm đất.
- Chứng minh rằng tổng năng lượng cơ học của vật được bảo toàn trong quá trình rơi.
- Bài Tập 2: Dao Động Con Lắc Đơn
- Tính thế năng của quả nặng tại điểm cao nhất của dao động.
- Tính động năng của quả nặng tại vị trí cân bằng.
- Chứng minh rằng tổng năng lượng của con lắc được bảo toàn trong quá trình dao động.
- Bài Tập 3: Ma Sát và Năng Lượng
- Tính công của lực ma sát khi xe trượt xuống.
- Tính sự mất mát năng lượng cơ học do ma sát.
- Tính vận tốc của xe khi đến chân mặt phẳng.
Một vật có khối lượng 2 kg được thả rơi tự do từ độ cao 10 m so với mặt đất. Bỏ qua lực cản không khí.
Một con lắc đơn có chiều dài 1 m và quả nặng 0.5 kg. Con lắc được kéo lệch khỏi vị trí cân bằng một góc nhỏ và thả ra.
Một xe trượt có khối lượng 3 kg trượt trên mặt phẳng nghiêng dài 5 m với góc nghiêng 30°. Hệ số ma sát giữa xe và mặt phẳng là 0.1.
XEM THÊM:
VI. Ứng Dụng Thực Tiễn Của Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng không chỉ là một nguyên lý cơ bản trong vật lý mà còn có những ứng dụng quan trọng trong nhiều lĩnh vực khoa học và đời sống. Dưới đây là một số ứng dụng tiêu biểu:
1. Trong ngành cơ khí và kỹ thuật
Trong ngành cơ khí, định luật bảo toàn năng lượng được sử dụng để thiết kế và tối ưu hóa các hệ thống máy móc. Ví dụ, động cơ nhiệt hoạt động dựa trên nguyên lý chuyển đổi nhiệt năng thành cơ năng, và quá trình này tuân theo định luật bảo toàn năng lượng. Các hệ thống này phải được thiết kế sao cho năng lượng mất mát do ma sát và các yếu tố khác là tối thiểu.
2. Trong ngành điện và năng lượng
Định luật bảo toàn năng lượng là cơ sở cho việc tính toán và vận hành các hệ thống điện. Các nhà máy điện chuyển hóa các dạng năng lượng khác như hóa năng, thủy năng, hoặc năng lượng mặt trời thành điện năng. Quá trình này đảm bảo rằng tổng năng lượng được bảo toàn, mặc dù có một phần năng lượng bị mất do nhiệt và các yếu tố khác.
3. Ứng dụng trong đời sống hàng ngày
Trong đời sống hàng ngày, định luật bảo toàn năng lượng được áp dụng rộng rãi. Một ví dụ phổ biến là việc sử dụng thiết bị gia dụng như tủ lạnh, lò vi sóng, hay điều hòa không khí. Những thiết bị này hoạt động dựa trên việc chuyển hóa năng lượng điện thành các dạng năng lượng khác như nhiệt hoặc cơ năng. Hiểu và áp dụng đúng định luật này giúp chúng ta sử dụng năng lượng hiệu quả hơn, giảm thiểu lãng phí.
Những ứng dụng trên chỉ là một phần nhỏ trong số vô vàn những ứng dụng thực tiễn của định luật bảo toàn năng lượng. Nguyên lý này đóng vai trò quan trọng trong việc phát triển các công nghệ hiện đại và trong việc duy trì cân bằng năng lượng toàn cầu.
VII. Các Nhà Khoa Học Đóng Góp Vào Định Luật Bảo Toàn Năng Lượng
Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản của vật lý học, được đóng góp và phát triển bởi nhiều nhà khoa học lỗi lạc từ thế kỷ XVIII đến thế kỷ XIX. Dưới đây là những nhà khoa học tiêu biểu đã góp phần vào sự ra đời và hoàn thiện của định luật này.
- Julius Robert von Mayer (1814-1878): Nhà vật lý người Đức, là một trong những người đầu tiên đề xuất khái niệm bảo toàn năng lượng. Năm 1842, Mayer đã phát hiện ra rằng năng lượng có thể chuyển hóa từ dạng này sang dạng khác, đặc biệt là từ công cơ học sang nhiệt năng, và ngược lại. Ông đã đóng góp quan trọng trong việc phát triển khái niệm đương lượng cơ của nhiệt, đặt nền tảng cho định luật bảo toàn năng lượng.
- James Prescott Joule (1818-1889): Nhà vật lý người Anh, nổi tiếng với thí nghiệm khuấy nước để chứng minh sự chuyển hóa năng lượng từ công thành nhiệt. Công trình của Joule vào năm 1845 đã khẳng định rằng năng lượng không tự nhiên mất đi mà chỉ chuyển hóa từ dạng này sang dạng khác. Từ đó, khái niệm đương lượng nhiệt của Joule trở thành một phần quan trọng của định luật bảo toàn năng lượng.
- Hermann von Helmholtz (1821-1894): Nhà vật lý và bác sĩ người Đức, đã mở rộng và phát triển lý thuyết về bảo toàn năng lượng. Năm 1847, ông công bố một luận án về sự bảo toàn năng lượng, trong đó nhấn mạnh rằng năng lượng trong vũ trụ là không đổi và có thể chuyển hóa qua lại giữa các dạng khác nhau như nhiệt, ánh sáng, và cơ năng. Công trình của Helmholtz đã củng cố và mở rộng ứng dụng của định luật bảo toàn năng lượng trong nhiều lĩnh vực khoa học.
- Antoine Lavoisier (1743-1794): Nhà hóa học người Pháp, được coi là cha đẻ của hóa học hiện đại. Ông là người đầu tiên đặt nền móng cho nguyên lý bảo toàn khối lượng, một tiền đề quan trọng cho việc hình thành định luật bảo toàn năng lượng. Lavoisier đã chứng minh rằng trong mọi phản ứng hóa học, tổng khối lượng của các chất phản ứng bằng tổng khối lượng của các sản phẩm tạo thành.
Các nhà khoa học này đã đóng vai trò không thể thiếu trong việc xác lập và hoàn thiện định luật bảo toàn năng lượng, mở ra những hiểu biết sâu sắc về sự chuyển hóa và bảo toàn năng lượng trong tự nhiên. Định luật này không chỉ là nền tảng của vật lý học mà còn ứng dụng rộng rãi trong hóa học, sinh học, và các ngành khoa học kỹ thuật khác.