Chủ đề 5 năng lực toán học: Khám phá 5 năng lực toán học quan trọng trong chương trình giáo dục phổ thông mới, giúp học sinh phát triển toàn diện từ tư duy logic đến kỹ năng giải quyết vấn đề thực tế, chuẩn bị hành trang vững chắc cho tương lai.
Mục lục
5 Năng Lực Toán Học - Tổng Hợp Chi Tiết
Trong chương trình giáo dục phổ thông mới, việc phát triển các năng lực toán học là mục tiêu quan trọng. Dưới đây là 5 năng lực toán học cần phát triển cho học sinh, cùng với các phương pháp dạy học phù hợp để hỗ trợ quá trình này.
I. Năng Lực Tư Duy và Lập Luận Toán Học
Năng lực này giúp học sinh phát triển khả năng suy luận logic, phát hiện và giải quyết các vấn đề toán học một cách có hệ thống.
- Bước 1: Phát hiện vấn đề toán học cần giải quyết.
- Bước 2: Sử dụng các nguyên lý toán học để phân tích vấn đề.
- Bước 3: Đưa ra kết luận và giải pháp phù hợp dựa trên lý thuyết toán học.
II. Năng Lực Mô Hình Hóa Toán Học
Năng lực này giúp học sinh có khả năng chuyển đổi các tình huống thực tế thành các mô hình toán học để giải quyết chúng.
- Bước 1: Xác định các yếu tố chính của vấn đề thực tế.
- Bước 2: Lập mô hình toán học tương ứng.
- Bước 3: Giải quyết vấn đề thông qua mô hình đã lập và kiểm tra tính hợp lý của kết quả.
III. Năng Lực Giải Quyết Vấn Đề Toán Học
Năng lực này tập trung vào việc giúp học sinh nhận diện và giải quyết các vấn đề toán học thông qua các bước cụ thể.
- Bước 1: Nhận diện vấn đề toán học cần giải quyết.
- Bước 2: Đề xuất cách tiếp cận và sử dụng các công cụ toán học phù hợp.
- Bước 3: Thực hiện giải pháp và đánh giá kết quả.
IV. Năng Lực Giao Tiếp Toán Học
Năng lực này giúp học sinh phát triển khả năng trình bày, thảo luận và giải thích các ý tưởng toán học.
- Chuyển đổi thông tin toán học thành văn bản hoặc lời nói dễ hiểu.
- Trình bày và diễn đạt các nội dung toán học trong các cuộc thảo luận.
- Thể hiện sự tự tin khi tranh luận và đánh giá các ý tưởng toán học.
V. Năng Lực Sử Dụng Công Cụ và Phương Tiện Học Toán
Năng lực này bao gồm kỹ năng sử dụng các công cụ hỗ trợ học toán như máy tính, que tính, hộp hình học,...
- Làm quen và sử dụng thành thạo các công cụ hỗ trợ học toán.
- Ứng dụng các phương tiện học toán trong việc giải quyết các bài toán thực tế.
- Phát triển khả năng sử dụng công nghệ thông tin trong học tập và giải toán.
VI. Phương Pháp Dạy Học Phát Triển 5 Năng Lực Toán Học
Để phát triển hiệu quả 5 năng lực toán học, cần áp dụng các phương pháp dạy học tích cực:
- Phương pháp trực quan: Sử dụng hình ảnh, video để giúp học sinh dễ dàng tiếp cận kiến thức.
- Phương pháp gợi mở – vấn đáp: Hướng dẫn học sinh tự tìm ra câu trả lời và phát triển tư duy phản biện.
- Phương pháp giải quyết vấn đề: Đặt học sinh vào các tình huống thực tế để tự tìm ra giải pháp.
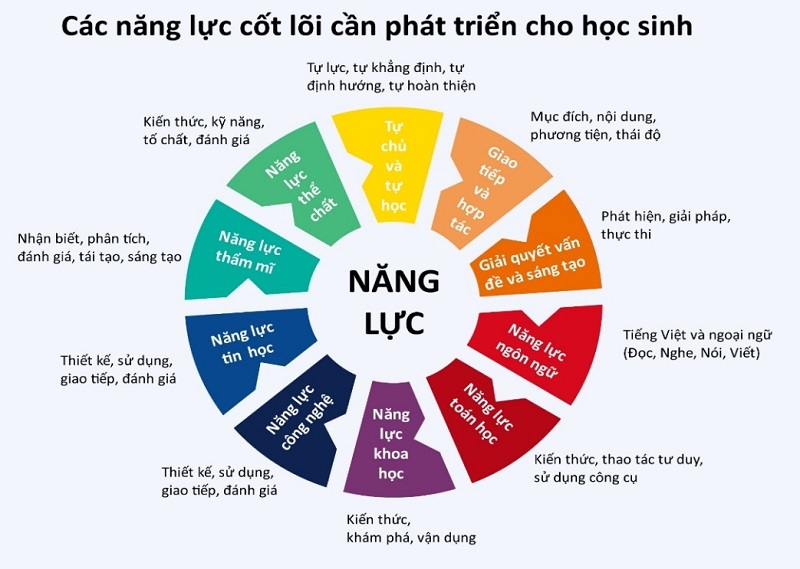
.png)
1. Năng lực tư duy và lập luận toán học
Năng lực tư duy và lập luận toán học là một trong những năng lực cốt lõi cần được phát triển trong chương trình giáo dục phổ thông mới. Đây là năng lực giúp học sinh hiểu sâu hơn về bản chất của các khái niệm toán học, biết cách tư duy logic, phân tích và giải quyết vấn đề một cách hệ thống.
1.1. Khái niệm và tầm quan trọng
Năng lực tư duy và lập luận toán học là khả năng sử dụng các quy luật, nguyên tắc toán học để phân tích, đánh giá và đưa ra kết luận. Đây là nền tảng để học sinh tiếp cận và hiểu sâu hơn về các kiến thức toán học, từ đó áp dụng vào thực tiễn một cách hiệu quả.
1.2. Phương pháp phát triển tư duy toán học
- Rèn luyện tư duy phản biện: Đặt câu hỏi, xem xét và đánh giá các giả thuyết, kết quả để phát triển khả năng phân tích, lập luận chặt chẽ.
- Sử dụng các bài toán có tính mở: Khuyến khích học sinh tìm ra nhiều cách giải quyết khác nhau, từ đó kích thích tư duy sáng tạo.
- Thực hành giải các bài toán thực tế: Giúp học sinh liên kết kiến thức với thực tiễn, từ đó phát triển kỹ năng lập luận toán học một cách tự nhiên.
1.3. Ứng dụng tư duy toán học trong đời sống
Tư duy và lập luận toán học không chỉ giới hạn trong việc giải các bài toán trên lớp mà còn được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau của đời sống như:
- Phân tích dữ liệu: Sử dụng toán học để phân tích, dự đoán xu hướng trong kinh tế, tài chính, và các lĩnh vực khác.
- Giải quyết vấn đề thực tiễn: Áp dụng các nguyên tắc toán học để giải quyết các vấn đề cụ thể như tính toán chi phí, tối ưu hóa quy trình sản xuất, hay lên kế hoạch công việc.
- Nâng cao khả năng tư duy logic: Việc thường xuyên rèn luyện tư duy toán học giúp cải thiện khả năng suy luận, ra quyết định một cách logic và hợp lý.
2. Năng lực mô hình hóa toán học
Năng lực mô hình hóa toán học là khả năng sử dụng các khái niệm, công cụ và phương pháp toán học để xây dựng, phân tích và giải quyết các tình huống trong đời sống thực tế. Việc phát triển năng lực này giúp học sinh không chỉ hiểu sâu hơn về các khái niệm toán học mà còn có khả năng áp dụng chúng vào thực tiễn, góp phần nâng cao khả năng giải quyết vấn đề một cách sáng tạo và hiệu quả.
2.1. Định nghĩa và quy trình thực hiện
Mô hình hóa toán học là quá trình chuyển đổi một vấn đề thực tiễn thành một bài toán toán học, sau đó sử dụng các phương pháp toán học để tìm ra lời giải và cuối cùng là đối chiếu kết quả với thực tế để đưa ra kết luận. Quy trình thực hiện mô hình hóa toán học thường bao gồm các bước sau:
- Nhận diện vấn đề: Xác định vấn đề cần giải quyết trong đời sống thực tế.
- Xây dựng mô hình toán học: Sử dụng các khái niệm toán học để biểu diễn vấn đề dưới dạng các phương trình, hàm số hoặc các mô hình khác.
- Giải quyết mô hình: Áp dụng các phương pháp toán học để giải quyết mô hình đã xây dựng.
- Phân tích và đánh giá: Đối chiếu kết quả với thực tế và điều chỉnh mô hình nếu cần thiết.
- Ứng dụng kết quả: Sử dụng kết quả giải quyết được để giải quyết vấn đề thực tiễn.
2.2. Ví dụ minh họa về mô hình hóa toán học
Để minh họa, hãy xem xét một bài toán thực tế: "Lập kế hoạch tối ưu hóa chi phí sản xuất một sản phẩm trong nhà máy." Bài toán này có thể được mô hình hóa như sau:
- Xác định các yếu tố liên quan: Chi phí sản xuất, số lượng sản phẩm, nguồn lực, thời gian sản xuất, v.v.
- Thiết lập các phương trình: Biểu diễn mối quan hệ giữa các yếu tố này bằng các phương trình toán học, chẳng hạn như phương trình tối ưu hóa.
- Giải bài toán: Sử dụng các phương pháp tối ưu hóa, chẳng hạn như phương pháp đơn hình, để tìm ra phương án tối ưu.
- Kiểm tra và điều chỉnh: Đối chiếu kết quả với thực tế và điều chỉnh mô hình nếu cần.
2.3. Tích hợp mô hình hóa trong giảng dạy
Để phát triển năng lực mô hình hóa toán học, việc tích hợp các bài toán mô hình hóa vào quá trình giảng dạy là rất quan trọng. Một số cách tiếp cận có thể bao gồm:
- Khuyến khích học sinh tham gia vào các bài toán thực tế, từ đó xây dựng các mô hình toán học.
- Sử dụng các công cụ hỗ trợ như phần mềm mô phỏng, biểu đồ, và các thiết bị đo lường để minh họa các mô hình toán học.
- Đưa ra các bài tập mô hình hóa từ đơn giản đến phức tạp, giúp học sinh dần dần nâng cao kỹ năng mô hình hóa.
Việc phát triển năng lực mô hình hóa toán học không chỉ giúp học sinh nắm vững kiến thức mà còn rèn luyện tư duy logic, khả năng phân tích và sáng tạo trong việc giải quyết các vấn đề thực tiễn.

3. Năng lực giải quyết vấn đề toán học
Năng lực giải quyết vấn đề toán học là một trong những năng lực cốt lõi được chú trọng trong chương trình giáo dục phổ thông mới. Mục tiêu của năng lực này là giúp học sinh không chỉ tiếp thu kiến thức toán học mà còn biết cách áp dụng chúng vào thực tế, từ đó phát triển tư duy logic, khả năng sáng tạo và kỹ năng xử lý vấn đề.
3.1. Các bước giải quyết vấn đề toán học
Để phát triển năng lực giải quyết vấn đề, học sinh cần thực hiện các bước sau:
- Nhận diện vấn đề: Học sinh cần xác định được vấn đề toán học cần giải quyết, hiểu rõ các yêu cầu và dữ liệu liên quan.
- Lập kế hoạch giải quyết: Sau khi xác định vấn đề, học sinh cần đề xuất các phương pháp và công cụ toán học có thể sử dụng để giải quyết vấn đề.
- Thực hiện giải pháp: Tiến hành giải quyết vấn đề theo kế hoạch đã đề ra, áp dụng các công thức, định lý toán học phù hợp.
- Đánh giá và phản hồi: Sau khi có kết quả, học sinh cần đánh giá lại tính chính xác của giải pháp, kiểm tra các khả năng xảy ra lỗi và khái quát hóa vấn đề để áp dụng cho các tình huống tương tự.
3.2. Phát triển kỹ năng thông qua bài tập thực tiễn
Bài tập thực tiễn đóng vai trò quan trọng trong việc rèn luyện và phát triển năng lực giải quyết vấn đề. Những bài tập này thường yêu cầu học sinh phải suy nghĩ sáng tạo, liên kết giữa lý thuyết và thực tế để tìm ra lời giải hợp lý. Ví dụ, khi học sinh giải quyết bài toán liên quan đến tính toán chi phí hoặc thiết kế mô hình, họ không chỉ áp dụng kiến thức toán học mà còn phải xem xét các yếu tố thực tế để đưa ra giải pháp tối ưu.
3.3. Phát huy sáng tạo trong giải quyết vấn đề
Phát huy sự sáng tạo là một yếu tố quan trọng trong quá trình giải quyết vấn đề toán học. Học sinh không chỉ dừng lại ở các phương pháp giải truyền thống mà còn cần tìm kiếm những cách tiếp cận mới, từ đó thúc đẩy khả năng tư duy và sáng tạo. Giáo viên cũng cần khuyến khích học sinh thử nghiệm các giải pháp khác nhau và đánh giá hiệu quả của từng phương án.

XEM THÊM:
4. Năng lực giao tiếp toán học
Năng lực giao tiếp toán học là khả năng sử dụng ngôn ngữ toán học để diễn đạt ý tưởng, trao đổi và thảo luận về các vấn đề toán học. Đây là một kỹ năng quan trọng giúp học sinh không chỉ hiểu mà còn truyền tải kiến thức toán học một cách chính xác và hiệu quả.
4.1. Kỹ năng trình bày và diễn đạt ý tưởng
Trong giao tiếp toán học, học sinh cần biết cách sử dụng ngôn ngữ toán học, ký hiệu, đồ thị, và các biểu đồ để trình bày rõ ràng và logic các ý tưởng của mình. Kỹ năng này giúp học sinh giải thích các bước giải toán, thảo luận về cách tiếp cận vấn đề và bảo vệ quan điểm của mình trước giáo viên và bạn bè.
4.2. Vai trò của giao tiếp trong học toán
Giao tiếp toán học không chỉ giúp học sinh hiểu sâu hơn về kiến thức mà còn thúc đẩy khả năng hợp tác trong học tập. Khi học sinh tham gia vào các hoạt động nhóm, thảo luận bài toán, họ có cơ hội lắng nghe, phản biện và học hỏi lẫn nhau, từ đó phát triển kỹ năng tư duy và sáng tạo.
4.3. Phương pháp rèn luyện giao tiếp toán học
Để rèn luyện năng lực giao tiếp toán học, học sinh cần thường xuyên tham gia vào các hoạt động thảo luận nhóm, giải thích cách giải các bài toán cho bạn bè và viết các báo cáo toán học. Giáo viên cũng nên khuyến khích học sinh trình bày các bài toán theo nhiều cách khác nhau, chẳng hạn như sử dụng sơ đồ, bảng biểu, hoặc diễn giải bằng lời.

5. Năng lực sử dụng công cụ, phương tiện học toán
Năng lực sử dụng công cụ và phương tiện học toán là một yếu tố quan trọng giúp học sinh tiếp cận và giải quyết các vấn đề toán học một cách hiệu quả. Việc này không chỉ đòi hỏi học sinh phải nắm vững cách sử dụng các công cụ, mà còn cần hiểu rõ cách áp dụng chúng trong các tình huống thực tế.
5.1. Giới thiệu các công cụ toán học phổ biến
- Máy tính cầm tay: Máy tính cầm tay là một công cụ quan trọng giúp học sinh thực hiện các phép tính phức tạp nhanh chóng và chính xác. Các loại máy tính hiện đại còn hỗ trợ vẽ đồ thị, giải phương trình và thực hiện các phép tính thống kê.
- Phần mềm toán học: Các phần mềm như GeoGebra, Maple, và Mathematica hỗ trợ việc vẽ hình, tính toán và mô phỏng các mô hình toán học, giúp học sinh hiểu sâu hơn về các khái niệm toán học trừu tượng.
- Bảng tương tác điện tử: Bảng tương tác điện tử cho phép giáo viên và học sinh tương tác trực tiếp với các nội dung toán học, giúp việc học trở nên sinh động và trực quan hơn.
5.2. Hướng dẫn sử dụng công cụ hiệu quả
- Hiểu rõ chức năng: Trước khi sử dụng bất kỳ công cụ nào, học sinh cần nắm rõ các chức năng cơ bản và cách thức vận hành của chúng. Điều này giúp tối ưu hóa quá trình giải quyết vấn đề.
- Áp dụng đúng tình huống: Mỗi công cụ có những điểm mạnh riêng, vì vậy học sinh cần lựa chọn công cụ phù hợp với bài toán cụ thể để đạt được kết quả tốt nhất.
- Luyện tập thường xuyên: Việc sử dụng thành thạo các công cụ yêu cầu sự luyện tập thường xuyên, qua đó giúp học sinh trở nên tự tin và linh hoạt trong việc áp dụng chúng vào các bài toán khác nhau.
5.3. Ứng dụng công cụ trong các bài toán thực tế
Việc áp dụng công cụ và phương tiện học toán vào các bài toán thực tế là cách tốt nhất để học sinh hiểu rõ giá trị của chúng. Chẳng hạn, trong việc giải các bài toán thống kê, học sinh có thể sử dụng máy tính cầm tay để xử lý dữ liệu nhanh chóng, hoặc sử dụng phần mềm toán học để mô phỏng các kịch bản khác nhau. Điều này không chỉ giúp tiết kiệm thời gian mà còn nâng cao tính chính xác của các phép toán.
Nhờ sự hỗ trợ của các công cụ, học sinh không chỉ đơn giản hóa được các phép toán phức tạp mà còn phát triển được tư duy logic và kỹ năng giải quyết vấn đề một cách toàn diện.

















