Thí Nghiệm Định Luật Bảo Toàn Động Lượng: Hiểu Rõ Hơn Qua Các Thí Nghiệm Thực Tế

Định luật bảo toàn động lượng là một trong những định luật cơ bản của vật lý, khẳng định rằng trong một hệ kín, tổng động lượng của hệ không thay đổi theo thời gian. Thí nghiệm về định luật này giúp học sinh hiểu rõ hơn về các khái niệm va chạm, động lượng, và hệ cô lập.

Mục đích của Thí Nghiệm

• Xác định động lượng của các vật trước và sau va chạm.
• Kiểm chứng định luật bảo toàn động lượng trong các trường hợp va chạm khác nhau: va chạm đàn hồi và va chạm mềm.

Dụng Cụ Thí Nghiệm

• Bàn trượt khí hoặc bề mặt phẳng ngang không ma sát.
• Các xe trượt có khối lượng khác nhau.
• Cảm biến đo tốc độ hoặc hệ thống ghi lại chuyển động.
• Bộ phận va chạm để tạo ra va chạm đàn hồi và va chạm mềm.

Cách Tiến Hành Thí Nghiệm

1. Đặt hai xe trượt trên bề mặt phẳng ngang không ma sát.
2. Thiết lập hệ thống đo để ghi lại tốc độ của các xe trước và sau va chạm.
3. Thực hiện va chạm đàn hồi giữa hai xe và ghi lại dữ liệu.
4. Thực hiện va chạm mềm (khi hai xe dính vào nhau sau va chạm) và ghi lại dữ liệu.

Kết Quả và Phân Tích

Sau khi thực hiện các thí nghiệm, dữ liệu thu được sẽ cho thấy rằng tổng động lượng của hệ trước và sau va chạm đều bằng nhau, khẳng định tính đúng đắn của định luật bảo toàn động lượng:

$$
p_trước=p_sau

Ứng Dụng Thực Tiễn

• Định luật bảo toàn động lượng được ứng dụng trong nhiều lĩnh vực như kỹ thuật, cơ khí, và hàng không.
• Hiểu biết về động lượng giúp cải tiến các thiết bị giảm chấn trong xe cộ, máy móc công nghiệp, và thậm chí là trong các trò chơi thể thao.

Kết Luận

Thí nghiệm về định luật bảo toàn động lượng là một phần quan trọng trong giáo dục vật lý, giúp học sinh nắm vững các khái niệm cơ bản và áp dụng chúng vào thực tiễn. Bằng cách này, họ có thể hiểu sâu hơn về các quy luật tự nhiên, từ đó phát triển kỹ năng tư duy logic và phân tích.

Động lượng là một đại lượng vật lý quan trọng, biểu thị cho sự chuyển động của vật thể và được định nghĩa bởi công thức:

\[
\vec{p} = m \cdot \vec{v}
\]

Trong đó:

• \(\vec{p}\) là động lượng (đơn vị: kg.m/s).
• \(m\) là khối lượng của vật (đơn vị: kg).
• \(\vec{v}\) là vận tốc của vật (đơn vị: m/s).

Định luật bảo toàn động lượng phát biểu rằng: Trong một hệ kín, không có lực ngoại lực tác dụng, tổng động lượng của hệ trước và sau khi xảy ra tương tác là không đổi. Cụ thể:

\[
\sum \vec{p}_{\text{trước}} = \sum \vec{p}_{\text{sau}}
\]

Để hiểu rõ hơn, hãy xét một hệ gồm hai vật thể va chạm vào nhau. Nếu:

• Vật thứ nhất có động lượng trước va chạm là \(\vec{p}_1\) và sau va chạm là \(\vec{p}_1'\).
• Vật thứ hai có động lượng trước va chạm là \(\vec{p}_2\) và sau va chạm là \(\vec{p}_2'\).

Thì định luật bảo toàn động lượng được viết dưới dạng:

\[
\vec{p}_1 + \vec{p}_2 = \vec{p}_1' + \vec{p}_2'
\]

Điều này có nghĩa là tổng động lượng của hai vật trước và sau va chạm là như nhau, miễn là không có lực ngoại lực tác động vào hệ.

Định luật này được ứng dụng rộng rãi trong nhiều lĩnh vực của vật lý và kỹ thuật, từ phân tích va chạm trong cơ học đến các hiện tượng trong động lực học chất lưu và cơ học lượng tử.

Để hiểu rõ hơn về định luật bảo toàn động lượng, các thí nghiệm thực tế là vô cùng quan trọng. Dưới đây là một số thí nghiệm phổ biến minh họa cho định luật này:

1. Thí Nghiệm Va Chạm Trên Đệm Không Khí

Trong thí nghiệm này, chúng ta sử dụng hai xe trượt trên đệm không khí để giảm thiểu ma sát. Các xe này va chạm với nhau và hệ số động lượng của chúng được đo trước và sau va chạm. Kết quả cho thấy tổng động lượng của hệ trước và sau va chạm là không đổi, xác nhận định luật bảo toàn động lượng.

2. Thí Nghiệm Va Chạm Đàn Hồi

Va chạm đàn hồi là khi hai vật va chạm và bật ngược lại mà không bị biến dạng vĩnh viễn. Thí nghiệm sử dụng hai viên bi trên mặt phẳng nhẵn, khi va chạm nhau, động lượng của chúng trước và sau va chạm được ghi lại và tính toán:

\[
\vec{p}_{\text{trước}} = \vec{p}_{\text{sau}}
\]

Kết quả chứng minh rằng tổng động lượng trước và sau va chạm của hai viên bi là bằng nhau.

3. Thí Nghiệm Va Chạm Không Đàn Hồi

Trong thí nghiệm này, hai vật thể va chạm và dính vào nhau sau va chạm. Ta xét trường hợp hai xe có khối lượng và vận tốc khác nhau. Động lượng được tính theo công thức:

\[
m_1 \vec{v}_1 + m_2 \vec{v}_2 = (m_1 + m_2)\vec{v}
\]

Thí nghiệm cho thấy rằng tổng động lượng của hệ trước và sau va chạm là không thay đổi, nhưng năng lượng có thể bị hao hụt do nhiệt hoặc biến dạng.

4. Thí Nghiệm Bắn Đạn Từ Súng

Một thí nghiệm nổi tiếng là bắn một viên đạn từ súng. Trước khi bắn, hệ (gồm súng và đạn) có động lượng bằng không. Sau khi bắn, động lượng của viên đạn và súng bằng nhau nhưng ngược chiều, chứng minh định luật bảo toàn động lượng:

\[
\vec{p}_{\text{súng}} = -\vec{p}_{\text{đạn}}
\]

Kết quả thí nghiệm giúp ta hiểu rõ hơn về nguyên lý hoạt động của súng và các hệ cơ học tương tự.

5. Ứng Dụng Thực Tế Của Định Luật Bảo Toàn Động Lượng

Định luật bảo toàn động lượng không chỉ có trong các thí nghiệm mà còn trong nhiều tình huống thực tế như phản lực của tên lửa, va chạm xe ô tô, và nhiều ứng dụng kỹ thuật khác. Những ví dụ này minh chứng rõ ràng cho tính đúng đắn và rộng rãi của định luật.

Để nắm vững định luật bảo toàn động lượng, cần hiểu rõ các dạng bài tập liên quan và cách áp dụng chúng vào thực tế. Dưới đây là các phân dạng bài tập thường gặp:

1. Bài Tập Về Xung Lực và Độ Biến Thiên Động Lượng

Xung lực và động lượng liên quan chặt chẽ với nhau, thường được sử dụng để giải các bài toán va chạm trong thời gian ngắn:

• Xác định xung lực tác dụng lên một vật khi biết lực tác dụng và thời gian tác dụng.
• Tính độ biến thiên động lượng dựa trên xung lực.

Ví dụ:

Cho lực \( F = 10 \, \text{N} \) tác dụng trong \( \Delta t = 2 \, \text{s} \). Tính xung lực và độ biến thiên động lượng.

2. Bài Tập Va Chạm Một Chiều

Va chạm một chiều thường đơn giản và dễ hiểu, áp dụng cho hai vật chuyển động dọc theo cùng một đường thẳng:

• Tìm vận tốc sau va chạm của hai vật khi biết khối lượng và vận tốc ban đầu.
• Xét va chạm đàn hồi và không đàn hồi.

Công thức cơ bản:

\[
m_1 v_1 + m_2 v_2 = m_1 v_1' + m_2 v_2'
\]

3. Bài Tập Va Chạm Hai Chiều

Va chạm hai chiều phức tạp hơn khi động lượng phải được bảo toàn theo hai hướng khác nhau:

• Phân tích động lượng theo hai trục vuông góc.
• Tính toán vận tốc và hướng chuyển động sau va chạm.

Ví dụ:

Hai quả bóng va chạm nhau trong mặt phẳng, tìm hướng và vận tốc của từng quả sau va chạm.

4. Ứng Dụng Định Luật Bảo Toàn Động Lượng Trong Đời Sống

Định luật bảo toàn động lượng có nhiều ứng dụng thực tế, giúp giải quyết các vấn đề trong kỹ thuật và đời sống:

• Phân tích va chạm xe cộ để xác định nguyên nhân tai nạn.
• Tính toán trong thiết kế tên lửa và động cơ phản lực.

Ví dụ:

Ứng dụng định luật để xác định vận tốc của một ô tô sau khi va chạm với một vật khác trên đường.

Những dạng bài tập trên không chỉ giúp hiểu rõ hơn về lý thuyết mà còn rèn luyện khả năng phân tích và giải quyết vấn đề thực tế.

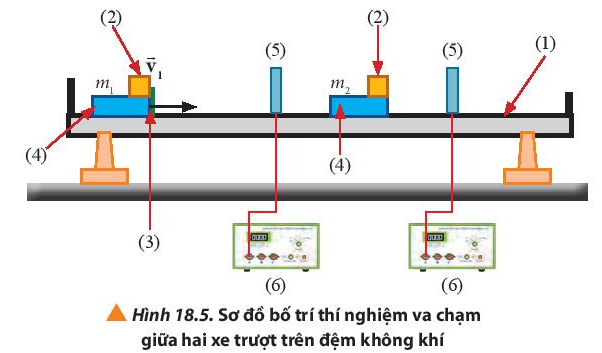
Thí nghiệm thực hành định luật bảo toàn động lượng giúp học sinh và sinh viên hiểu rõ hơn về nguyên lý này thông qua các kết quả thực tế. Dưới đây là các bước tiến hành thí nghiệm và phân tích kết quả:

1. Chuẩn Bị Dụng Cụ Thí Nghiệm

• Một bộ đệm không khí để giảm ma sát.
• Hai xe trượt có khối lượng khác nhau.
• Bộ cảm biến quang học để đo vận tốc trước và sau va chạm.
• Máy tính hoặc thiết bị ghi dữ liệu để phân tích kết quả.

2. Tiến Hành Thí Nghiệm

1. Đặt hai xe trượt trên đệm không khí sao cho chúng không bị ma sát làm chậm lại.
2. Kích hoạt hệ thống và để một xe trượt về phía xe kia.
3. Sử dụng cảm biến để đo vận tốc của cả hai xe trước và sau va chạm.
4. Ghi lại các giá trị vận tốc và khối lượng của từng xe.

3. Phân Tích Kết Quả

Sau khi thu thập dữ liệu, tiến hành phân tích động lượng của hệ:

\[
\text{Động lượng trước va chạm: } \vec{p}_{\text{trước}} = m_1 \cdot v_1 + m_2 \cdot v_2
\]

\[
\text{Động lượng sau va chạm: } \vec{p}_{\text{sau}} = m_1 \cdot v_1' + m_2 \cdot v_2'
\]

So sánh hai giá trị này, ta có thể kết luận về sự bảo toàn động lượng trong thí nghiệm. Nếu \(\vec{p}_{\text{trước}} \approx \vec{p}_{\text{sau}}\), điều này chứng minh rằng động lượng được bảo toàn trong va chạm, phù hợp với lý thuyết.

4. Kết Quả và So Sánh Thực Nghiệm

Kết quả của thí nghiệm thường cho thấy sai số nhỏ do các yếu tố như ma sát còn sót lại hoặc sai số thiết bị. Tuy nhiên, kết quả chung thường khẳng định rằng động lượng của hệ trước và sau va chạm là gần như tương đương, minh chứng cho định luật bảo toàn động lượng.

Thí nghiệm này không chỉ giúp hiểu rõ hơn về lý thuyết mà còn phát triển kỹ năng thực hành và phân tích dữ liệu khoa học.