Chủ đề nội dung định luật bảo toàn động lượng: Bài viết này cung cấp một cái nhìn toàn diện về động lượng và định luật bảo toàn động lượng, từ lý thuyết cơ bản đến các bài tập thực hành. Bạn sẽ tìm thấy hướng dẫn chi tiết và các phương pháp giải bài tập hiệu quả, giúp nắm vững kiến thức và ứng dụng vào thực tế.
Mục lục
Bài Tập Động Lượng và Định Luật Bảo Toàn Động Lượng
Động lượng và định luật bảo toàn động lượng là những khái niệm quan trọng trong vật lý học, đặc biệt là trong cơ học. Các bài tập về động lượng giúp học sinh hiểu rõ hơn về sự tương tác giữa các vật thể trong các hệ kín. Dưới đây là tổng hợp các bài tập phổ biến liên quan đến chủ đề này.
1. Bài Tập Tính Động Lượng
- Ví dụ: Một quả bóng có khối lượng 1kg rơi tự do xuống đất trong 0,5 giây. Tính độ biến thiên động lượng của quả bóng trong khoảng thời gian đó. Biết rằng gia tốc trọng trường g = 10 m/s2.
- Giải pháp: Sử dụng công thức động lượng \( p = mv \), trong đó \( v \) là vận tốc và \( m \) là khối lượng.
2. Bài Tập Va Chạm
- Ví dụ: Một viên đạn có khối lượng 2kg bay thẳng đứng với vận tốc 500m/s sau khi nổ. Hãy xác định hướng bay của mảnh đạn còn lại.
- Giải pháp: Sử dụng định luật bảo toàn động lượng để tìm vận tốc và hướng của mảnh đạn thứ hai.
3. Bài Tập Về Độ Biến Thiên Động Lượng
- Ví dụ: Một quả bóng đá có khối lượng 300g va chạm vào tường với vận tốc 5m/s và nảy trở lại với cùng vận tốc. Tính độ biến thiên động lượng của quả bóng.
- Giải pháp: Độ biến thiên động lượng \( \Delta p \) được tính bằng \( \Delta p = p_{sau} - p_{trước} \).
4. Bài Tập Về Động Lượng Của Hệ
- Ví dụ: Hai vật có khối lượng lần lượt là 1kg và 3kg chuyển động với vận tốc 3m/s và 1m/s. Tính tổng động lượng của hệ trong các trường hợp: cùng hướng, ngược chiều và vuông góc.
- Giải pháp: Tổng động lượng của hệ là tổng của từng động lượng thành phần, xét theo các trường hợp hướng khác nhau.
5. Bài Tập Phân Tích Động Lượng Trong Chuyển Động Phản Lực
- Ví dụ: Một khẩu pháo có khối lượng 130kg bắn một viên bi 1kg với vận tốc 400m/s. Tính vận tốc của khẩu pháo sau khi bắn.
- Giải pháp: Sử dụng định luật bảo toàn động lượng trong hệ kín để tìm vận tốc của khẩu pháo.
Kết Luận
Các bài tập về động lượng và định luật bảo toàn động lượng không chỉ giúp học sinh nắm vững kiến thức lý thuyết mà còn phát triển khả năng giải quyết vấn đề thực tiễn. Việc luyện tập thường xuyên với các dạng bài tập đa dạng sẽ giúp học sinh tự tin hơn trong việc ứng dụng kiến thức vật lý vào cuộc sống.

.png)
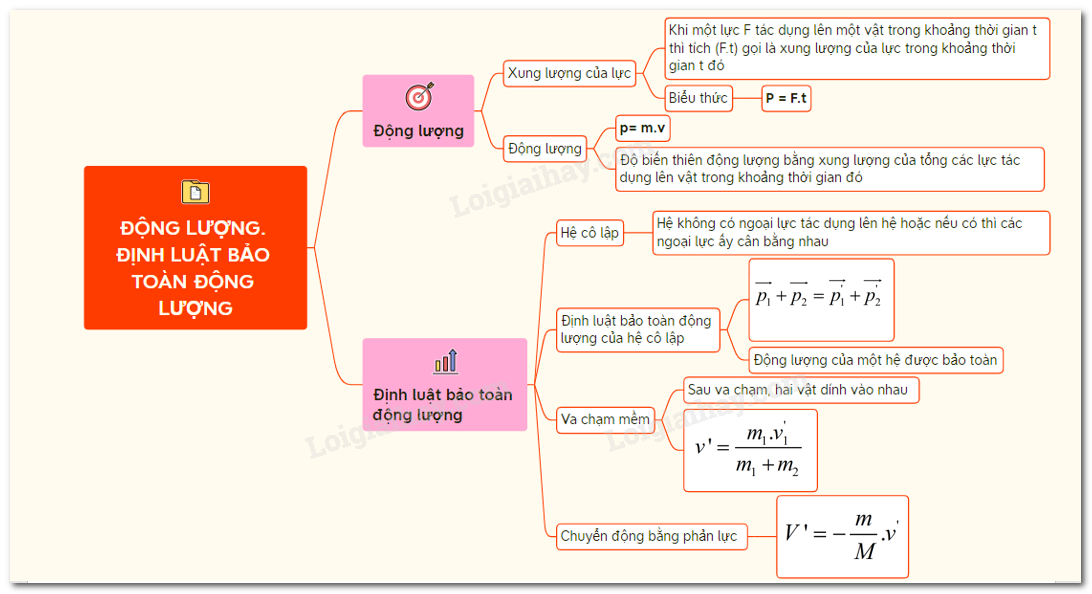
Tổng Quan Về Động Lượng và Định Luật Bảo Toàn Động Lượng
Động lượng là một đại lượng vật lý quan trọng, được định nghĩa là tích của khối lượng và vận tốc của một vật thể. Động lượng của một vật thể được biểu diễn bằng công thức:
\[ \mathbf{p} = m \times \mathbf{v} \]
Trong đó:
- \( \mathbf{p} \) là động lượng (kg·m/s)
- \( m \) là khối lượng của vật thể (kg)
- \( \mathbf{v} \) là vận tốc của vật thể (m/s)
Định luật bảo toàn động lượng phát biểu rằng: "Trong một hệ kín (không có lực bên ngoài tác dụng), tổng động lượng của hệ trước và sau va chạm luôn bằng nhau." Đây là một nguyên lý cơ bản trong cơ học và được sử dụng rộng rãi trong các bài tập tính toán liên quan đến va chạm và tương tác giữa các vật thể.
Để hiểu rõ hơn về định luật bảo toàn động lượng, hãy xem xét một số ví dụ về các trường hợp va chạm:
- Va chạm đàn hồi: Động lượng và năng lượng của hệ đều được bảo toàn. Ví dụ như va chạm giữa hai quả bóng bi-a.
- Va chạm không đàn hồi: Động lượng được bảo toàn nhưng một phần năng lượng chuyển hóa thành nhiệt hoặc dạng năng lượng khác. Ví dụ, khi xe ô tô va chạm và dính vào nhau.
Các bài tập về động lượng và định luật bảo toàn động lượng thường liên quan đến việc tính toán các giá trị động lượng trước và sau va chạm, xác định vận tốc hoặc khối lượng của các vật thể tham gia tương tác. Bằng cách áp dụng các công thức và định lý liên quan, học sinh có thể giải quyết các bài toán phức tạp một cách chính xác.
Các Dạng Bài Tập Về Động Lượng
Các bài tập về động lượng thường được chia thành nhiều dạng khác nhau, mỗi dạng đều yêu cầu áp dụng các nguyên tắc cơ bản của động lượng và định luật bảo toàn động lượng để giải quyết. Dưới đây là một số dạng bài tập phổ biến:
- Bài Tập Tính Động Lượng Cơ Bản: Dạng bài tập này yêu cầu tính toán động lượng của một vật thể khi biết khối lượng và vận tốc của nó. Công thức sử dụng là \( \mathbf{p} = m \times \mathbf{v} \).
- Bài Tập Về Va Chạm Đàn Hồi: Trong các bài tập này, động lượng và năng lượng của hệ đều được bảo toàn. Ví dụ, tính toán vận tốc của hai vật sau khi va chạm hoặc xác định một trong hai khối lượng nếu các thông số khác đã biết.
- Bài Tập Về Va Chạm Không Đàn Hồi: Dạng bài tập này tập trung vào các tình huống mà động lượng được bảo toàn nhưng một phần năng lượng chuyển hóa thành nhiệt hoặc năng lượng khác. Thường gặp trong các bài toán va chạm mà các vật dính vào nhau sau va chạm.
- Bài Tập Về Độ Biến Thiên Động Lượng: Dạng bài tập này yêu cầu tính toán sự thay đổi của động lượng trong quá trình va chạm hoặc khi một lực tác dụng lên vật thể trong một khoảng thời gian. Công thức liên quan bao gồm \( \Delta \mathbf{p} = F \times \Delta t \).
- Bài Tập Về Chuyển Động Phản Lực: Đây là dạng bài tập liên quan đến nguyên tắc bảo toàn động lượng trong các tình huống mà vật thể phóng ra một phần khối lượng, như tên lửa phóng lên hoặc súng bắn đạn.
Để giải quyết các dạng bài tập này, học sinh cần nắm vững các khái niệm cơ bản và biết cách áp dụng chúng vào từng bài toán cụ thể. Bằng cách luyện tập qua nhiều dạng bài tập khác nhau, kỹ năng giải quyết vấn đề sẽ được nâng cao đáng kể.

Phương Pháp Giải Bài Tập Động Lượng
Khi giải bài tập động lượng, việc tuân thủ một quy trình logic và có phương pháp sẽ giúp bạn dễ dàng tiếp cận và giải quyết bài toán một cách hiệu quả. Dưới đây là các bước cơ bản trong phương pháp giải bài tập động lượng:
- Phân tích bài toán: Đầu tiên, hãy đọc kỹ đề bài để hiểu rõ các thông tin được cung cấp và yêu cầu của bài toán. Xác định các đại lượng vật lý liên quan như khối lượng, vận tốc, lực tác dụng, và thời gian.
- Vẽ sơ đồ minh họa: Vẽ sơ đồ hoặc biểu đồ để minh họa các lực, vận tốc và các yếu tố khác tác động lên vật thể. Điều này giúp bạn hình dung rõ hơn về tình huống vật lý đang xảy ra.
- Áp dụng định luật bảo toàn động lượng: Sử dụng định luật bảo toàn động lượng, công thức cơ bản là: \[ m_1 \times v_1 + m_2 \times v_2 = m_1 \times v_1' + m_2 \times v_2' \] Trong đó, \( m_1 \) và \( m_2 \) là khối lượng của các vật, \( v_1 \) và \( v_2 \) là vận tốc ban đầu, còn \( v_1' \) và \( v_2' \) là vận tốc sau va chạm.
- Giải hệ phương trình: Dựa vào các công thức vật lý và dữ liệu đã xác định, lập và giải các phương trình để tìm ra các đại lượng chưa biết. Có thể sử dụng các phương pháp đại số hoặc đồ thị tùy vào bài toán cụ thể.
- Kiểm tra kết quả: Sau khi tính toán, hãy kiểm tra lại các kết quả xem chúng có hợp lý và phù hợp với tình huống vật lý hay không. Đảm bảo rằng đơn vị của các đại lượng đã được tính toán chính xác.
- Viết kết luận: Cuối cùng, trình bày rõ ràng kết quả cuối cùng của bài toán, giải thích ngắn gọn quá trình giải và khẳng định tính hợp lý của kết quả.
Việc luyện tập thường xuyên và áp dụng đúng phương pháp sẽ giúp bạn trở nên thành thạo trong việc giải các bài tập động lượng, từ đó nắm vững kiến thức vật lý một cách toàn diện.
Ứng Dụng Thực Tiễn Của Động Lượng và Định Luật Bảo Toàn Động Lượng
Động lượng và định luật bảo toàn động lượng là những khái niệm cơ bản trong vật lý, có nhiều ứng dụng quan trọng trong cuộc sống hàng ngày cũng như trong các ngành công nghiệp khác nhau. Dưới đây là một số ứng dụng thực tiễn nổi bật:
- Va chạm trong giao thông: Khi xảy ra va chạm giữa các phương tiện, định luật bảo toàn động lượng giúp các nhà khoa học xác định lực tác động, dự đoán thiệt hại và nghiên cứu các giải pháp giảm thiểu tai nạn.
- Thiết kế tên lửa và tàu vũ trụ: Động lượng được ứng dụng trong việc tính toán quỹ đạo và tốc độ của tên lửa khi rời khỏi mặt đất, đảm bảo chúng di chuyển đúng hướng và đạt đến điểm đích an toàn.
- Thể thao: Trong các môn thể thao như bóng đá, bóng rổ, việc kiểm soát động lượng của bóng và vận động viên là yếu tố quyết định đến kết quả của trận đấu. Ví dụ, khi đá bóng, cầu thủ phải tính toán động lượng để quả bóng đi đúng hướng và lực sút mong muốn.
- Điều tra tai nạn: Định luật bảo toàn động lượng còn được ứng dụng trong việc điều tra các vụ tai nạn để tái tạo lại hiện trường, từ đó tìm ra nguyên nhân và trách nhiệm của các bên liên quan.
- Robot và tự động hóa: Động lượng được áp dụng trong lập trình chuyển động của robot để chúng có thể di chuyển mượt mà và thực hiện các nhiệm vụ một cách chính xác. Trong sản xuất, các cánh tay robot cũng sử dụng nguyên lý này để di chuyển các vật thể với độ chính xác cao.
Như vậy, động lượng và định luật bảo toàn động lượng không chỉ là những khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tiễn, góp phần quan trọng vào sự phát triển của khoa học kỹ thuật và đời sống con người.

Những Lưu Ý Khi Giải Bài Tập Động Lượng
Để giải bài tập về động lượng hiệu quả, người học cần chú ý đến một số yếu tố quan trọng nhằm tránh những sai lầm thường gặp và đảm bảo kết quả chính xác. Dưới đây là những lưu ý cụ thể:
- Xác định hệ kín: Hãy đảm bảo rằng hệ thống bạn đang xét là hệ kín, nghĩa là không có lực bên ngoài tác động. Điều này rất quan trọng để áp dụng định luật bảo toàn động lượng một cách chính xác.
- Phân tích các lực tác động: Khi phân tích bài toán, cần xác định rõ các lực tác động lên vật thể và hướng di chuyển của chúng. Đừng quên xét cả các lực nội tại và ngoại tại, vì chúng có thể ảnh hưởng đến kết quả tính toán.
- Chú ý đến hướng của động lượng: Động lượng là đại lượng vectơ, vì vậy hướng của động lượng phải được xem xét cẩn thận. Khi cộng động lượng của các vật thể, cần cộng các vectơ theo đúng hướng của chúng.
- Kiểm tra đơn vị: Luôn luôn kiểm tra các đơn vị đo trong quá trình tính toán. Đảm bảo rằng tất cả các đại lượng đều sử dụng cùng một hệ đơn vị để tránh nhầm lẫn dẫn đến kết quả sai lệch.
- Sử dụng định luật bảo toàn động lượng: Khi gặp bài toán va chạm, hãy sử dụng định luật bảo toàn động lượng để giải. Đối với va chạm đàn hồi, động năng cũng được bảo toàn; còn với va chạm không đàn hồi, chỉ động lượng được bảo toàn.
- Kiểm tra kết quả: Sau khi tính toán, hãy kiểm tra lại kết quả bằng cách so sánh với điều kiện ban đầu hoặc bằng cách sử dụng một phương pháp giải khác nếu có thể.
Những lưu ý trên sẽ giúp bạn giải quyết các bài tập động lượng một cách chính xác và hiệu quả, đồng thời tránh được những lỗi phổ biến trong quá trình học tập.