Định Luật Bảo Toàn Năng Lượng Tiếng Anh: Khám Phá Chi Tiết và Ứng Dụng

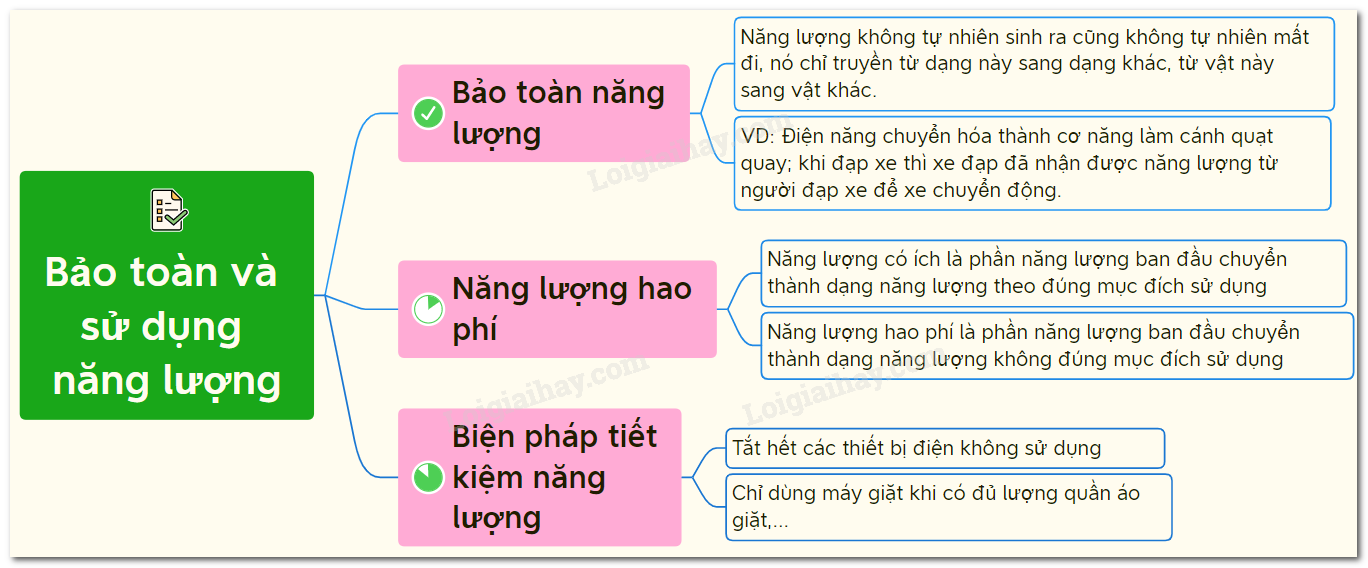
Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản của vật lý học, phát biểu rằng tổng năng lượng trong một hệ kín luôn được bảo toàn theo thời gian. Điều này có nghĩa là năng lượng không thể tự nhiên sinh ra hoặc mất đi, mà chỉ có thể chuyển đổi từ dạng này sang dạng khác.

1. Khái Niệm Định Luật Bảo Toàn Năng Lượng

Trong tiếng Anh, định luật bảo toàn năng lượng được gọi là "Law of Conservation of Energy". Công thức tổng quát biểu diễn định luật này như sau:

\[E_{\text{tổng}} = E_k + E_p = \text{const}\]

• \(E_k = \frac{1}{2}mv^2\): Động năng, với \(m\) là khối lượng và \(v\) là vận tốc.
• \(E_p = mgh\): Thế năng hấp dẫn, với \(h\) là độ cao so với mốc thế năng, \(g\) là gia tốc trọng trường.

Tổng năng lượng \(E_{\text{tổng}}\) của hệ được tính bằng tổng động năng và thế năng, và giá trị này luôn không đổi trong quá trình chuyển động của hệ kín.

2. Ứng Dụng Của Định Luật Bảo Toàn Năng Lượng

Định luật bảo toàn năng lượng có rất nhiều ứng dụng trong các lĩnh vực khác nhau của vật lý và kỹ thuật:

• Cơ học: Giúp tính toán các quá trình va chạm, chuyển động, và tính lực tác động lên vật.
• Nhiệt động lực học: Sử dụng để phân tích các quá trình nhiệt như trong động cơ nhiệt, hệ thống làm lạnh.
• Điện học: Ứng dụng trong việc tính toán công suất điện, mạch điện và năng lượng tiêu thụ.
• Kỹ thuật: Được sử dụng trong thiết kế và phân tích các hệ thống máy móc, từ máy phát điện đến động cơ, đảm bảo rằng năng lượng đầu vào và đầu ra của hệ thống được cân bằng.
• Ngành công nghệ năng lượng tái tạo: Định luật bảo toàn năng lượng được áp dụng để tối ưu hóa việc chuyển đổi năng lượng từ nguồn tái tạo như năng lượng mặt trời, gió và thủy điện thành điện năng hiệu quả nhất.
• Y học và Sinh học: Trong y học, định luật này được sử dụng để hiểu quá trình trao đổi chất và năng lượng trong cơ thể sống, từ đó hỗ trợ phát triển các phương pháp điều trị và phục hồi chức năng.

3. Ví Dụ Về Bảo Toàn Năng Lượng

Dưới đây là một ví dụ minh họa về định luật bảo toàn năng lượng:

Giả sử một vật có khối lượng \(m\) rơi từ độ cao \(h\). Ban đầu, vật có thế năng \(E_p = mgh\) và động năng bằng không. Khi vật rơi xuống, thế năng giảm đi và chuyển hóa thành động năng \(E_k = \frac{1}{2}mv^2\). Khi vật chạm đất, toàn bộ thế năng đã chuyển thành động năng. Tổng năng lượng của vật trước và sau khi rơi vẫn không thay đổi, minh chứng cho định luật bảo toàn năng lượng.

4. Các Dạng Bài Tập Về Định Luật Bảo Toàn Năng Lượng

Dưới đây là một số dạng bài tập phổ biến liên quan đến định luật bảo toàn năng lượng:

1. Tính động năng và thế năng của một vật tại các vị trí khác nhau.
2. Giải các bài toán về va chạm đàn hồi và không đàn hồi.
3. Phân tích sự chuyển đổi năng lượng trong các hệ cơ học phức tạp.

5. Lợi Ích Của Việc Nắm Vững Định Luật Bảo Toàn Năng Lượng

• Hiểu rõ nguyên lý này giúp giải quyết nhiều bài toán vật lý phức tạp.
• Cải thiện khả năng phân tích và áp dụng kiến thức vật lý vào thực tế.
• Giúp học sinh, sinh viên đạt kết quả cao trong các kỳ thi liên quan đến vật lý.
• Ứng dụng trong nhiều ngành nghề như kỹ thuật, công nghệ năng lượng, và y học, giúp tối ưu hóa quy trình làm việc và phát triển công nghệ mới.

6. Kết Luận

Định luật bảo toàn năng lượng là nền tảng quan trọng trong vật lý học và có nhiều ứng dụng thực tiễn trong cuộc sống. Việc nắm vững định luật này không chỉ giúp nâng cao kiến thức mà còn mở ra nhiều cơ hội nghiên cứu và ứng dụng trong các lĩnh vực khoa học và kỹ thuật.

Định luật bảo toàn năng lượng, hay còn gọi là nguyên lý thứ nhất của nhiệt động lực học, là một trong những quy luật cơ bản của vật lý học. Định luật này phát biểu rằng:

• Năng lượng không tự sinh ra và không tự mất đi: Tổng năng lượng trong một hệ cô lập luôn được bảo toàn. Năng lượng có thể chuyển từ dạng này sang dạng khác, nhưng tổng lượng năng lượng luôn không đổi.
• Công thức cơ bản: Định luật được diễn đạt bằng công thức:
  ΔU = Q - A
  Trong đó:
  • ΔU là sự thay đổi nội năng của hệ.
  • Q là nhiệt lượng cung cấp cho hệ.
  • A là công hệ thực hiện lên môi trường xung quanh.
• Ý nghĩa của định luật: Định luật bảo toàn năng lượng là cơ sở cho nhiều nguyên lý và định luật khác trong vật lý, như nguyên lý bảo toàn cơ năng, và là nền tảng cho sự phát triển của nhiều ngành khoa học và công nghệ.

Định luật này không chỉ có ý nghĩa lý thuyết mà còn có nhiều ứng dụng thực tiễn, giúp giải thích và dự đoán các hiện tượng tự nhiên, đồng thời phát triển các công nghệ hiện đại.

Quá trình biến đổi năng lượng là một trong những khía cạnh cốt lõi của Định luật Bảo toàn Năng lượng. Theo định luật này, năng lượng không tự nhiên sinh ra hay mất đi, mà chỉ có thể chuyển hóa từ dạng này sang dạng khác. Trong mọi quá trình, từ cơ học đến hóa học, năng lượng luôn được bảo toàn.

Khi một hệ thống trải qua một quá trình biến đổi, năng lượng có thể thay đổi từ dạng này sang dạng khác. Ví dụ, trong một hệ cơ học, thế năng có thể biến đổi thành động năng, và ngược lại:

• Khi vật thể di chuyển từ độ cao lớn xuống thấp, thế năng giảm đi, và đồng thời động năng tăng lên.
• Ngược lại, khi vật thể di chuyển lên cao, động năng giảm đi trong khi thế năng tăng lên.

Biểu thức bảo toàn cơ năng:

Ví dụ khác về quá trình biến đổi năng lượng có thể thấy trong các hệ thống nhiệt động lực học, nơi năng lượng nhiệt được chuyển đổi thành công cơ học, hoặc trong quá trình phân rã hạt nhân, nơi năng lượng liên kết hạt nhân được chuyển thành năng lượng khác.

Những quá trình này chứng minh rằng dù năng lượng thay đổi hình thức, tổng năng lượng trong hệ kín vẫn luôn được bảo toàn.

Định luật Bảo toàn Năng lượng không chỉ là một nguyên lý cơ bản trong vật lý mà còn có nhiều ứng dụng thực tiễn quan trọng trong cuộc sống và công nghệ. Dưới đây là một số ví dụ điển hình về cách định luật này được áp dụng:

• Hệ thống năng lượng mặt trời: Các tấm pin mặt trời chuyển hóa năng lượng ánh sáng thành điện năng. Quá trình này dựa trên nguyên lý bảo toàn năng lượng, nơi năng lượng ánh sáng được chuyển hóa trực tiếp thành năng lượng điện mà không bị mất đi.
• Động cơ nhiệt: Động cơ xe hơi và các loại động cơ nhiệt khác hoạt động dựa trên sự chuyển hóa năng lượng nhiệt thành công cơ học. Định luật bảo toàn năng lượng đảm bảo rằng năng lượng nhiệt từ nhiên liệu không biến mất mà được chuyển hóa thành động năng của xe.
• Hệ thống điện: Trong hệ thống điện, năng lượng điện được chuyển hóa thành năng lượng cơ học, nhiệt năng, hoặc năng lượng ánh sáng mà không làm mất đi tổng năng lượng ban đầu.
• Ứng dụng trong công nghệ hạt nhân: Quá trình phân hạch hạt nhân giải phóng năng lượng lớn, tuân theo định luật bảo toàn năng lượng, nơi năng lượng liên kết hạt nhân được chuyển hóa thành năng lượng nhiệt và bức xạ.

Nhờ vào định luật bảo toàn năng lượng, chúng ta có thể thiết kế và tối ưu hóa các hệ thống công nghệ để sử dụng năng lượng hiệu quả hơn, giảm thiểu lãng phí và tối đa hóa hiệu suất.

Các bài tập vận dụng định luật bảo toàn năng lượng là một cách tuyệt vời để củng cố hiểu biết và khả năng áp dụng của bạn vào các tình huống thực tế. Dưới đây là một số bài tập giúp bạn thực hành và nắm vững hơn về định luật này.

• Bài tập 1: Một vật có khối lượng 2kg rơi tự do từ độ cao 10m. Tính vận tốc của vật khi chạm đất và năng lượng bị mất mát do lực cản.
• Bài tập 2: Vật có khối lượng 5kg trượt không ma sát trên một mặt phẳng nghiêng có độ dốc 30°. Tính vận tốc của vật ở chân mặt phẳng nghiêng.
• Bài tập 3: Một con lắc đơn có độ dài dây 2m. Tính vận tốc của quả cầu khi nó đi qua vị trí thấp nhất của đường cong.
• Bài tập 4: Vật có khối lượng 3kg được ném ngang với vận tốc ban đầu 10m/s. Tính độ cao cực đại mà vật đạt được và thời gian để vật chạm đất.

Những bài tập này không chỉ giúp bạn hiểu rõ hơn về lý thuyết mà còn giúp bạn phát triển kỹ năng giải quyết các vấn đề phức tạp.