Ba Điện Tích Điểm: Hiểu Rõ Từ A Đến Z Về Nguyên Lý Và Ứng Dụng

Ba điện tích điểm là khái niệm cơ bản trong vật lý điện trường, thường được nghiên cứu trong bối cảnh điện tích được đặt tại các đỉnh của các hình học như tam giác hoặc hình vuông. Dưới đây là một số nội dung liên quan đến chủ đề này:

1. Điện Trường Tại Các Đỉnh Tam Giác

Khi ba điện tích được đặt tại ba đỉnh của một tam giác, chúng tạo ra các điện trường và lực điện tác động lẫn nhau. Cụ thể, với tam giác đều, điện trường tại tâm của tam giác có thể được tính toán bằng cách sử dụng định lý cosin và các công thức liên quan.

Công thức tổng quát cho cường độ điện trường tại tâm tam giác:

\[
E = \frac{1}{4\pi\epsilon_0} \cdot \sum_{i=1}^{3} \frac{q_i}{r_i^2}
\]
trong đó:

• \(q_i\) là giá trị của từng điện tích.
• \(r_i\) là khoảng cách từ điện tích đó đến điểm cần tính điện trường.
• \(\epsilon_0\) là hằng số điện môi của môi trường.

2. Lực Điện Tác Dụng Lên Điện Tích

Đối với các điện tích đặt tại ba đỉnh của tam giác vuông, lực điện tổng hợp tác dụng lên mỗi điện tích có thể được xác định bằng việc áp dụng định lý Pythagore và các công thức cosin để tính góc giữa các lực. Điều này đặc biệt hữu ích trong việc dự đoán hướng và độ lớn của lực tác động.

3. Bài Toán Ứng Dụng

Một bài toán điển hình liên quan đến ba điện tích điểm là tìm lực điện tổng hợp tác dụng lên một điện tích tại một trong các đỉnh của tam giác. Phương pháp giải thường bao gồm:

• Xác định độ lớn của từng lực.
• Sử dụng các công thức vector để tìm tổng hợp lực.
• Tính toán góc lệch để xác định hướng của lực tổng hợp.

Các bài toán này không chỉ giúp hiểu rõ hơn về nguyên lý điện trường mà còn rèn luyện kỹ năng giải toán phức tạp trong vật lý.

Kết Luận

Chủ đề "ba điện tích điểm" là một nội dung quan trọng trong học tập và nghiên cứu vật lý, đặc biệt là phần điện trường và lực điện. Việc nắm vững kiến thức này sẽ giúp ích trong việc giải quyết các bài toán liên quan đến điện tích trong thực tế.

Ba điện tích điểm là một khái niệm quan trọng trong điện học, đặc biệt khi nghiên cứu về lực điện và điện trường. Điện tích điểm được hiểu là một điện tích rất nhỏ, đến mức có thể coi như một điểm trong không gian mà không có kích thước. Khi ba điện tích điểm được đặt trong một hệ thống, chúng tương tác với nhau tạo nên các hiện tượng điện từ đáng chú ý. Dưới đây là các khái niệm cơ bản liên quan đến ba điện tích điểm:

• Điện tích điểm: Là một điện tích có kích thước rất nhỏ, không có hình dạng cụ thể và được coi như một điểm trong không gian.
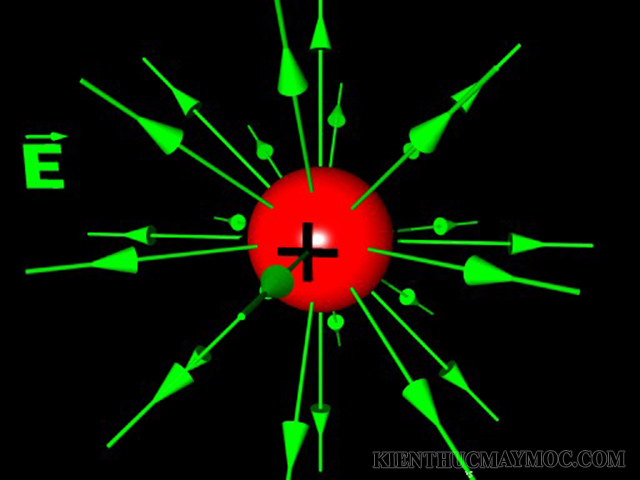
• Điện trường: Là vùng không gian xung quanh một điện tích điểm, trong đó các điện tích khác sẽ chịu lực tác động của điện tích đó.
• Lực Coulomb: Là lực hút hoặc đẩy giữa hai điện tích điểm, được xác định bởi định luật Coulomb. Công thức tính lực Coulomb giữa hai điện tích điểm là:

  \[
  F = k \cdot \frac{|q_1 \cdot q_2|}{r^2}
  \]
  trong đó:
  

  
  
  • \(F\) là lực giữa hai điện tích.
  
  
  • \(q_1\) và \(q_2\) là độ lớn của hai điện tích.
  
  
  • \(r\) là khoảng cách giữa hai điện tích.
  
  
  • \(k\) là hằng số Coulomb.
  
  
  
  


• Điện thế: Là năng lượng cần thiết để di chuyển một điện tích điểm trong một điện trường từ vị trí này đến vị trí khác. Điện thế tại một điểm trong điện trường được xác định bằng công thức:

  \[
  V = k \cdot \frac{q}{r}
  \]
  trong đó:
  

  
  
  • \(V\) là điện thế tại điểm cần tính.
  
  
  • \(q\) là độ lớn của điện tích.
  
  
  • \(r\) là khoảng cách từ điện tích đến điểm cần tính điện thế.
  
  
  
  

Trong trường hợp ba điện tích điểm, sự tương tác giữa chúng tạo ra một hệ thống phức tạp với nhiều lực và điện trường khác nhau. Những khái niệm này không chỉ là nền tảng của điện học mà còn có ứng dụng rộng rãi trong thực tế và công nghệ.

Điện trường tại một điểm trong không gian do ba điện tích điểm gây ra là kết quả của sự chồng chất các điện trường riêng lẻ từ từng điện tích. Để tính toán điện trường tổng hợp tại một điểm, chúng ta cần thực hiện các bước sau:

1. Xác định tọa độ của các điện tích điểm và điểm cần tính điện trường: Giả sử ba điện tích có độ lớn lần lượt là \(q_1\), \(q_2\), và \(q_3\) được đặt tại các vị trí \(A(x_1, y_1)\), \(B(x_2, y_2)\), và \(C(x_3, y_3)\). Điểm cần tính điện trường có tọa độ \(P(x, y)\).
2. Tính các vectơ điện trường do từng điện tích gây ra: Điện trường do mỗi điện tích \(q_i\) (với \(i = 1, 2, 3\)) tại điểm \(P\) được xác định theo công thức:

   
   \[
   \vec{E}_i = k \cdot \frac{q_i}{r_i^2} \cdot \hat{r}_i
   \]
   trong đó:
   

   
   
   • \(\vec{E}_i\) là vectơ điện trường do điện tích \(q_i\) gây ra tại điểm \(P\).
   
   
   • \(k\) là hằng số Coulomb.
   
   
   • \(r_i\) là khoảng cách từ \(q_i\) đến \(P\), được tính bằng công thức:
     \[
     r_i = \sqrt{(x - x_i)^2 + (y - y_i)^2}
     \]
     
   
   
   • \(\hat{r}_i\) là vectơ đơn vị chỉ hướng từ \(q_i\) đến \(P\).
   
   
   
   


3. Chồng chất các vectơ điện trường: Tổng hợp điện trường tại điểm \(P\) là tổng vectơ của các điện trường do từng điện tích điểm gây ra:

   
   \[
   \vec{E}_{\text{tổng}} = \vec{E}_1 + \vec{E}_2 + \vec{E}_3
   \]

   Các thành phần của vectơ tổng hợp được tính bằng cách cộng các thành phần x và y của từng vectơ điện trường.
4. Tính toán độ lớn và hướng của điện trường tổng hợp: Độ lớn của điện trường tổng hợp tại \(P\) được xác định bằng công thức:

   
   \[
   E_{\text{tổng}} = \sqrt{(E_{\text{tổng},x})^2 + (E_{\text{tổng},y})^2}
   \]

   Hướng của điện trường tổng hợp được xác định bằng góc \(\theta\) so với trục x, với:

   
   \[
   \theta = \tan^{-1} \left(\frac{E_{\text{tổng},y}}{E_{\text{tổng},x}}\right)
   \]

Việc tính toán điện trường do ba điện tích điểm gây ra yêu cầu sự kết hợp giữa các công thức toán học và khả năng phân tích vectơ. Đây là một ứng dụng quan trọng trong các bài toán liên quan đến lực điện và điện trường trong vật lý.

Lực điện tổng hợp là lực kết hợp của các lực điện trường tác dụng lên một điện tích điểm do các điện tích khác trong hệ thống gây ra. Để tính toán lực điện tổng hợp trong hệ thống ba điện tích điểm, chúng ta cần hiểu rõ về định luật Coulomb và nguyên lý chồng chất lực.

3.1 Lực điện trong tam giác đều

Xét ba điện tích điểm \(q_1\), \(q_2\), và \(q_3\) đặt tại ba đỉnh của một tam giác đều cạnh \(a\). Các lực điện tác dụng lên mỗi điện tích đều có độ lớn bằng nhau do tam giác đều có các cạnh bằng nhau. Độ lớn của mỗi lực điện giữa hai điện tích được tính theo công thức Coulomb:

\[ F = k \cdot \frac{|q_1 \cdot q_2|}{a^2} \]

Trong tam giác đều, lực tổng hợp tác dụng lên một điện tích bất kỳ được tính bằng cách tổng hợp vector của hai lực còn lại. Do các lực này có cùng độ lớn và góc giữa chúng là 120°, ta có thể dùng quy tắc hình bình hành để tính lực tổng hợp.

Độ lớn của lực tổng hợp \(F_\text{tổng}\) được tính bằng:

\[ F_\text{tổng} = F \cdot \sqrt{3} \]

Lực này hướng từ đỉnh tam giác về phía tâm của tam giác.

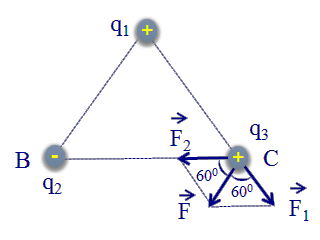
3.2 Lực điện trong tam giác vuông

Khi ba điện tích được đặt tại ba đỉnh của một tam giác vuông, lực tổng hợp sẽ có đặc điểm khác. Ví dụ, xét tam giác vuông ABC với hai cạnh vuông góc AB và BC, và các điện tích tương ứng là \(q_1\) tại A, \(q_2\) tại B, và \(q_3\) tại C.

Lực điện tổng hợp tác dụng lên \(q_3\) sẽ là tổng của hai lực do \(q_1\) và \(q_2\) tác dụng. Ta có thể tính từng lực đơn lẻ rồi cộng lại theo vector:

\[ F_3 = \sqrt{F_{31}^2 + F_{32}^2} \]

Trong đó, \(F_{31}\) và \(F_{32}\) là các lực do \(q_1\) và \(q_2\) tác dụng lên \(q_3\). Góc giữa các lực này là 90°.

3.3 Phương pháp giải bài toán lực điện tổng hợp

• Xác định các điện tích và khoảng cách giữa chúng.
• Tính các lực đơn lẻ giữa từng cặp điện tích bằng định luật Coulomb.
• Sử dụng nguyên lý chồng chất để tính toán lực tổng hợp, thường bằng cách cộng vector các lực.
• Xác định hướng của lực tổng hợp, dựa trên tính đối xứng hoặc sử dụng các công cụ hình học như tam giác vuông hay hình bình hành.

Phương pháp này có thể được áp dụng cho mọi dạng bài toán liên quan đến ba điện tích điểm, giúp xác định lực điện tổng hợp một cách hiệu quả và chính xác.

Khái niệm về ba điện tích điểm không chỉ là một bài toán lý thuyết mà còn có nhiều ứng dụng thực tiễn quan trọng trong các lĩnh vực khoa học và công nghệ. Dưới đây là một số ứng dụng tiêu biểu của lý thuyết này:

4.1 Bài toán thực tế liên quan đến điện tích điểm

Trong thực tế, việc xác định lực tương tác giữa ba điện tích điểm có thể giúp chúng ta hiểu rõ hơn về các hiện tượng điện từ, ví dụ như trong nghiên cứu cấu trúc nguyên tử, nơi mà các hạt mang điện như proton và electron tương tác với nhau. Khái niệm ba điện tích điểm cũng giúp giải thích các hiện tượng như sự hình thành của các phân tử trong hóa học, khi ba nguyên tử liên kết với nhau dưới tác động của các lực Coulomb.

4.2 Ứng dụng trong công nghệ và đời sống

Các ứng dụng của lý thuyết ba điện tích điểm trong công nghệ bao gồm:

• Thiết kế tụ điện: Trong các tụ điện, các điện tích điểm là cơ sở để tính toán và tối ưu hóa hiệu suất lưu trữ năng lượng. Tụ điện được ứng dụng rộng rãi trong các thiết bị điện tử như điện thoại, máy tính và hệ thống điện.
• Máy phát điện và động cơ: Nguyên lý của ba điện tích điểm giúp thiết kế các máy phát điện và động cơ hiệu quả hơn bằng cách tối ưu hóa lực điện trường và tương tác giữa các điện tích.
• Công nghệ vi mạch: Trong các vi mạch điện tử, việc quản lý và điều khiển các điện tích điểm là yếu tố quan trọng để đảm bảo hoạt động chính xác và hiệu quả của các linh kiện như transistor và diode.
• Thiết bị y tế: Trong y học, lý thuyết này giúp phát triển các thiết bị chẩn đoán hình ảnh như MRI, nơi mà các điện tích điểm trong cơ thể tạo ra các tín hiệu mà máy móc có thể đọc được để tạo ra hình ảnh chi tiết của các mô và cơ quan bên trong.

Như vậy, lý thuyết ba điện tích điểm không chỉ dừng lại ở việc giải các bài toán lý thuyết mà còn có nhiều ứng dụng thiết thực, đóng góp to lớn vào sự phát triển của các ngành khoa học và công nghệ.

Dưới đây là một số bài tập tiêu biểu về ba điện tích điểm, giúp củng cố kiến thức và áp dụng các lý thuyết đã học.

5.1 Bài tập xác định lực và điện trường

Bài tập 1: Ba điện tích điểm \( q_1 = 2 \times 10^{-6} \, \text{C} \), \( q_2 = -3 \times 10^{-6} \, \text{C} \), và \( q_3 = 4 \times 10^{-6} \, \text{C} \) được đặt tại ba đỉnh của một tam giác đều cạnh \( a = 0,1 \, \text{m} \). Hãy xác định lực điện tác dụng lên điện tích \( q_1 \).

1. Xác định các vector lực điện tác dụng lên \( q_1 \) do \( q_2 \) và \( q_3 \) gây ra:
• Lực \( \mathbf{F}_{12} \) do \( q_2 \) gây ra: \[ F_{12} = k \cdot \frac{|q_1 \cdot q_2|}{a^2} \]
• Lực \( \mathbf{F}_{13} \) do \( q_3 \) gây ra: \[ F_{13} = k \cdot \frac{|q_1 \cdot q_3|}{a^2} \]
2. Tính tổng hợp lực \( \mathbf{F}_{1} \) bằng cách cộng vector các lực \( \mathbf{F}_{12} \) và \( \mathbf{F}_{13} \).

Bài tập 2: Ba điện tích điểm được đặt tại các đỉnh của một tam giác vuông có các cạnh vuông góc \( a = 0,3 \, \text{m} \) và \( b = 0,4 \, \text{m} \). Hãy xác định điện trường tại đỉnh còn lại.

1. Xác định các vector điện trường tại đỉnh tam giác:
• Điện trường \( \mathbf{E}_1 \) do \( q_1 \) gây ra: \[ E_1 = k \cdot \frac{|q_1|}{r_1^2} \]
• Điện trường \( \mathbf{E}_2 \) do \( q_2 \) gây ra: \[ E_2 = k \cdot \frac{|q_2|}{r_2^2} \]
2. Tính tổng hợp điện trường \( \mathbf{E}_{\text{total}} \) bằng cách cộng vector các điện trường \( \mathbf{E}_1 \) và \( \mathbf{E}_2 \).

5.2 Bài tập tổng hợp lực điện

Bài tập 1: Ba điện tích \( q_1 \), \( q_2 \), và \( q_3 \) được đặt tại các đỉnh của một tam giác đều. Tính tổng hợp lực điện tác dụng lên mỗi điện tích.

1. Sử dụng định lý cos để tính góc giữa các lực điện:
• Tính lực điện giữa các cặp điện tích: \[ F_{ij} = k \cdot \frac{|q_i \cdot q_j|}{r_{ij}^2} \]
2. Sử dụng phương pháp hình học hoặc vector để tính tổng hợp lực tác dụng lên từng điện tích.

Bài tập 2: Ba điện tích được đặt trên các đỉnh của một tam giác vuông cân có cạnh góc vuông \( a = 0,2 \, \text{m} \). Hãy tính tổng hợp lực điện tác dụng lên đỉnh có điện tích dương.

1. Tính lực điện do từng điện tích tác dụng lên điện tích tại đỉnh cần tính:
• Lực \( \mathbf{F}_{12} \) giữa \( q_1 \) và \( q_2 \): \[ F_{12} = k \cdot \frac{|q_1 \cdot q_2|}{a^2} \]
• Lực \( \mathbf{F}_{13} \) giữa \( q_1 \) và \( q_3 \): \[ F_{13} = k \cdot \frac{|q_1 \cdot q_3|}{r^2} \]
2. Sử dụng phương pháp vector để tổng hợp lực điện.

5.3 Bài tập ứng dụng nâng cao

Bài tập 1: Xác định vị trí mà một điện tích thứ tư phải được đặt để hệ thống các điện tích này đạt trạng thái cân bằng.

1. Xác định tổng lực điện tác dụng lên điện tích thứ tư và đặt nó bằng không.
2. Giải hệ phương trình để tìm vị trí cần đặt điện tích.

Bài tập 2: Tìm giá trị của các điện tích để tổng lực điện tác dụng lên một trong ba điện tích bằng không.

1. Đặt điều kiện tổng lực điện bằng không và giải phương trình tương ứng.