2 Lực Đồng Quy: Khái Niệm, Ứng Dụng và Cách Tính Hợp Lực

Trong vật lý, hai lực đồng quy là hai lực có điểm đặt tại cùng một điểm và có thể được tổng hợp thành một lực duy nhất gọi là hợp lực. Quy tắc hình bình hành là phương pháp phổ biến nhất để xác định hợp lực này.

Quy tắc hình bình hành

• Để tổng hợp hai lực đồng quy, trước tiên, ta trượt hai vectơ lực trên giá của chúng đến điểm đồng quy.
• Sau đó, áp dụng quy tắc hình bình hành để tìm hợp lực.
• Trong quy tắc này, hai lực đồng quy được biểu diễn dưới dạng hai cạnh kề của một hình bình hành, và đường chéo của hình này sẽ là hợp lực cần tìm.

Công thức tính độ lớn của hợp lực dựa trên định lý cosin:

\[
F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha}
\]

Trong đó:

• \(F_1\) và \(F_2\) là độ lớn của hai lực thành phần.
• \(\alpha\) là góc hợp bởi hai lực đồng quy.

Các trường hợp đặc biệt

1. Nếu hai lực đồng quy cùng phương và cùng chiều, hợp lực sẽ có độ lớn bằng tổng hai lực thành phần:

   
   \[
   F = F_1 + F_2
   \]

2. Nếu hai lực đồng quy cùng phương nhưng ngược chiều, hợp lực sẽ có độ lớn bằng hiệu độ lớn hai lực thành phần:

   
   \[
   F = |F_1 - F_2|
   \]

3. Nếu hai lực đồng quy vuông góc với nhau, hợp lực sẽ được tính bằng công thức Pythagore:

   
   \[
   F = \sqrt{F_1^2 + F_2^2}
   \]

Ứng dụng thực tế

Quy tắc tổng hợp lực đồng quy được áp dụng rộng rãi trong các bài toán vật lý liên quan đến cân bằng lực, động lực học của vật rắn, và thiết kế kỹ thuật. Hiểu rõ và sử dụng thành thạo quy tắc này giúp giải quyết nhanh chóng các bài toán liên quan đến lực trong không gian hai chiều.

Hãy lưu ý rằng việc phân tích lực cũng có thể được thực hiện bằng cách phân tích hợp lực thành các thành phần lực theo phương ngang và phương thẳng đứng, giúp dễ dàng giải quyết các bài toán phức tạp hơn.

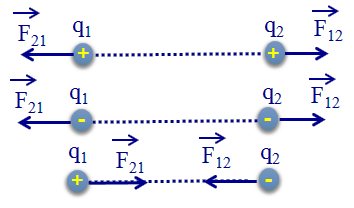
Lực đồng quy là khái niệm cơ bản trong vật lý, mô tả tình huống khi hai hoặc nhiều lực tác dụng lên cùng một điểm. Điểm này được gọi là điểm đồng quy, và các lực tác động được gọi là lực đồng quy.

• Điểm đồng quy: Là điểm mà tất cả các lực đồng quy đều tác động lên. Đây là điểm chung mà các vectơ lực gặp nhau.
• Vectơ lực: Mỗi lực đồng quy được biểu diễn bằng một vectơ, có phương, chiều và độ lớn xác định. Vectơ lực có thể được trượt dọc theo giá của nó đến điểm đồng quy mà không thay đổi tác dụng của lực.

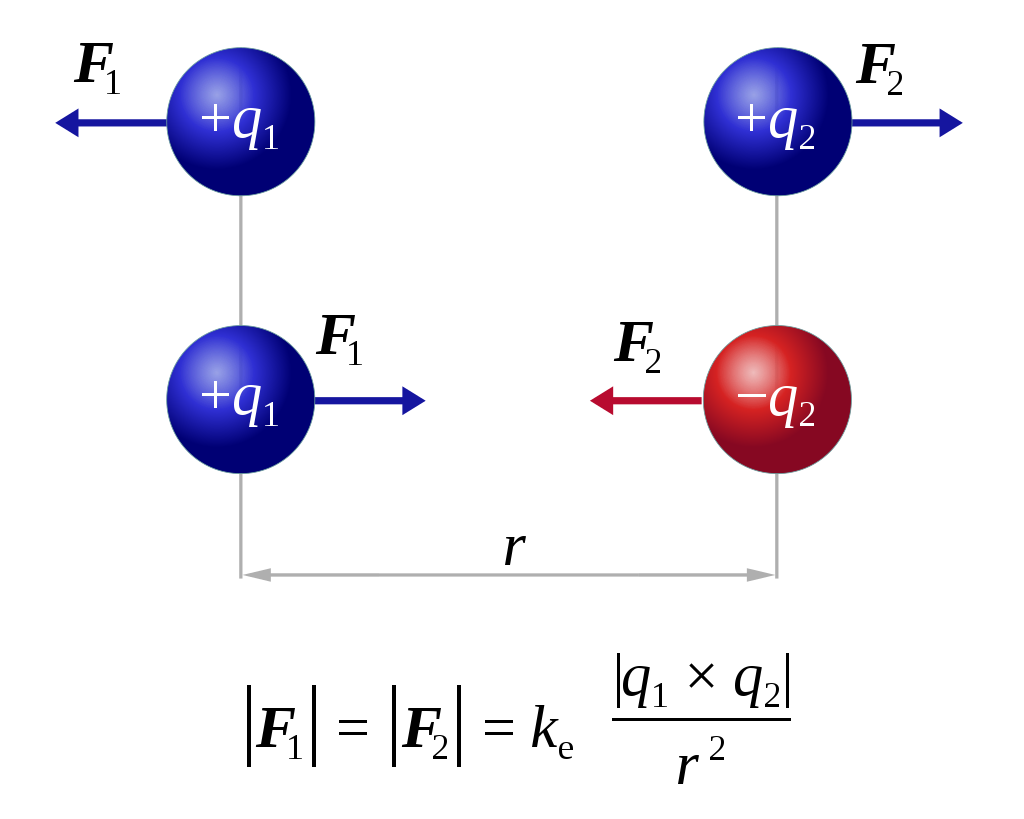
Khi hai lực đồng quy tác dụng lên một điểm, hợp lực của chúng được xác định bằng quy tắc hình bình hành. Đây là phương pháp hình học dùng để cộng hai vectơ lực.

Công thức tính hợp lực:

\[
\vec{F} = \vec{F_1} + \vec{F_2}
\]

Độ lớn của hợp lực được tính bằng định lý cosin:

\[
F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha}
\]

Trong đó:

• \(F_1\) và \(F_2\) là độ lớn của hai lực thành phần.
• \(\alpha\) là góc giữa hai lực đồng quy.

Nhờ vào khái niệm lực đồng quy và quy tắc hình bình hành, chúng ta có thể dễ dàng xác định hướng và độ lớn của hợp lực tác dụng lên một vật, giúp giải quyết nhiều bài toán vật lý và ứng dụng thực tiễn trong cuộc sống hàng ngày.

Quy tắc hình bình hành là một phương pháp hình học được sử dụng để tổng hợp hai lực đồng quy tác dụng lên cùng một điểm. Phương pháp này giúp xác định hợp lực của hai lực một cách trực quan và chính xác.

1. Bước 1: Xác định hai lực cần tổng hợp.

   Mỗi lực được biểu diễn dưới dạng một vectơ, có độ lớn và phương hướng cụ thể.

2. Bước 2: Vẽ các vectơ lực từ điểm đồng quy.

   Trượt hai vectơ lực trên giá của chúng sao cho chúng cùng bắt đầu từ điểm đồng quy. Vectơ lực thứ nhất được vẽ trước, vectơ lực thứ hai được vẽ bắt đầu từ đầu mút của vectơ lực thứ nhất.

3. Bước 3: Vẽ hình bình hành.

   Hoàn thiện hình bình hành bằng cách vẽ các đường song song với hai vectơ lực từ các đầu mút của chúng.

4. Bước 4: Xác định hợp lực.

   Hợp lực là đường chéo của hình bình hành, bắt đầu từ điểm đồng quy. Độ lớn và phương hướng của hợp lực được xác định bởi chiều dài và hướng của đường chéo này.

Công thức tính độ lớn của hợp lực:

\[
F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha}
\]

Trong đó:

• \(F_1\) và \(F_2\) là độ lớn của hai lực thành phần.
• \(\alpha\) là góc giữa hai lực đồng quy.

Quy tắc hình bình hành không chỉ giúp xác định hợp lực mà còn cung cấp cái nhìn trực quan về cách hai lực kết hợp với nhau. Phương pháp này được sử dụng rộng rãi trong các bài toán vật lý và trong các ứng dụng kỹ thuật thực tiễn.

Lực đồng quy có nhiều trường hợp đặc biệt, mỗi trường hợp đều có các tính chất và cách tính toán riêng biệt. Dưới đây là các trường hợp phổ biến khi hai lực đồng quy tác dụng lên một điểm:

1. Hai lực đồng quy cùng phương và cùng chiều:

   Trong trường hợp này, hai lực có cùng phương và hướng về cùng một phía. Hợp lực của chúng sẽ có độ lớn bằng tổng độ lớn của hai lực thành phần và cùng phương với các lực đó:

   
   \[
   F = F_1 + F_2
   \]

2. Hai lực đồng quy cùng phương nhưng ngược chiều:

   Khi hai lực đồng quy có cùng phương nhưng ngược chiều, hợp lực sẽ có độ lớn bằng hiệu tuyệt đối của hai lực thành phần và cùng phương với lực lớn hơn:

   
   \[
   F = |F_1 - F_2|
   \]

3. Hai lực đồng quy vuông góc với nhau:

   Nếu hai lực đồng quy tạo với nhau một góc 90°, hợp lực sẽ được tính bằng công thức Pythagore:

   
   \[
   F = \sqrt{F_1^2 + F_2^2}
   \]

4. Hai lực đồng quy tạo một góc bất kỳ:

   Trường hợp tổng quát nhất là khi hai lực đồng quy tạo với nhau một góc bất kỳ \(\alpha\). Hợp lực trong trường hợp này được tính theo định lý cosin:

   
   \[
   F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha}
   \]

Những trường hợp đặc biệt này giúp đơn giản hóa quá trình tính toán và phân tích lực trong nhiều tình huống thực tiễn, đặc biệt trong các bài toán vật lý và kỹ thuật. Việc hiểu rõ từng trường hợp cụ thể sẽ giúp bạn áp dụng đúng phương pháp để xác định hợp lực một cách chính xác và nhanh chóng.

Lực đồng quy không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng thực tiễn trong cuộc sống và kỹ thuật. Dưới đây là một số ứng dụng nổi bật:

1. Thiết kế và xây dựng công trình:

   Trong xây dựng, việc xác định lực đồng quy rất quan trọng để đảm bảo sự cân bằng và ổn định của các kết cấu. Các kỹ sư thường tính toán lực đồng quy để thiết kế các cấu trúc như cầu, tòa nhà, và tháp, đảm bảo rằng các lực tác dụng lên các điểm kết cấu sẽ không làm cho công trình bị biến dạng hoặc sụp đổ.

2. Động lực học của vật rắn:

   Trong cơ học, lực đồng quy giúp phân tích chuyển động và sự cân bằng của các vật thể rắn. Bằng cách tổng hợp các lực đồng quy, chúng ta có thể xác định được các điều kiện cân bằng hoặc chuyển động của vật, từ đó dự đoán được hành vi của vật trong các hệ thống cơ học phức tạp.

3. Thiết kế máy móc và thiết bị:

   Trong công nghiệp, các kỹ sư sử dụng lực đồng quy để thiết kế các bộ phận máy móc chịu tác động của nhiều lực cùng lúc, như trong các hệ thống truyền động, cánh tay robot, và cơ cấu đòn bẩy. Việc hiểu rõ các lực đồng quy giúp tối ưu hóa thiết kế, đảm bảo hiệu suất và độ bền của thiết bị.

4. Phân tích lực trong thể thao:

   Trong thể thao, lực đồng quy được sử dụng để phân tích chuyển động và tối ưu hóa kỹ thuật của vận động viên. Ví dụ, trong môn nhảy xa, việc tổng hợp các lực đồng quy giúp huấn luyện viên hiểu rõ hơn về cách vận động viên có thể tối đa hóa khoảng cách nhảy của mình.

5. Các ứng dụng trong đời sống hàng ngày:

   Trong cuộc sống hàng ngày, chúng ta cũng sử dụng nguyên lý của lực đồng quy mà không nhận ra, chẳng hạn khi treo tranh, bố trí đồ đạc để cân bằng trên mặt phẳng, hoặc thậm chí khi kéo hoặc đẩy các vật nặng theo nhiều hướng khác nhau.

Các ứng dụng này cho thấy tầm quan trọng của lực đồng quy trong nhiều lĩnh vực khác nhau, từ xây dựng và công nghiệp đến thể thao và đời sống hàng ngày. Việc hiểu rõ và áp dụng đúng khái niệm này giúp tối ưu hóa hiệu quả công việc và nâng cao chất lượng cuộc sống.

Phân tích lực đồng quy là quá trình tách một lực thành hai hoặc nhiều lực thành phần đồng quy với nhau. Các lực này thường vuông góc hoặc song song, giúp đơn giản hóa việc giải các bài toán liên quan đến cân bằng lực hoặc chuyển động. Dưới đây là các bước cơ bản để phân tích lực đồng quy:

1. Bước 1: Xác định lực cần phân tích.

   Giả sử có một lực \(\vec{F}\) tác dụng lên một điểm. Lực này cần được phân tích thành hai lực thành phần đồng quy.

2. Bước 2: Lựa chọn phương và chiều của các lực thành phần.

   Thông thường, các lực thành phần được chọn theo hai phương vuông góc nhau (ví dụ: trục Ox và Oy). Điều này giúp việc tính toán trở nên dễ dàng hơn.

3. Bước 3: Áp dụng các định lý lượng giác để xác định các lực thành phần.

   Sử dụng các công thức lượng giác để tính toán độ lớn của các lực thành phần:

   
   \[
   F_x = F \cdot \cos\theta
   \]

   
   \[
   F_y = F \cdot \sin\theta
   \]

   Trong đó:

   • \(F_x\) và \(F_y\) là độ lớn của các lực thành phần theo trục Ox và Oy.
   • \(\theta\) là góc giữa lực \(\vec{F}\) và trục Ox.
4. Bước 4: Kiểm tra kết quả phân tích.

   Sau khi xác định được các lực thành phần, hãy kiểm tra lại bằng cách cộng chúng để đảm bảo rằng tổng hợp của chúng chính là lực ban đầu \(\vec{F}\):

   
   \[
   \vec{F} = \vec{F_x} + \vec{F_y}
   \]

Phân tích lực đồng quy là kỹ thuật quan trọng trong vật lý và kỹ thuật, giúp hiểu rõ hơn về sự tương tác của các lực trong hệ thống và giải quyết các bài toán liên quan đến cân bằng hoặc chuyển động một cách hiệu quả.