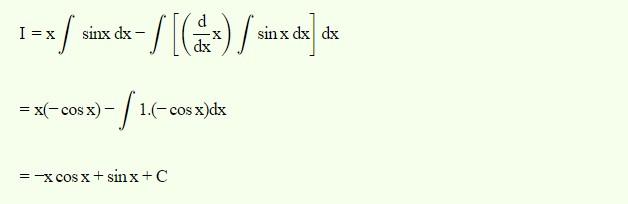Tổng hợp các công thức đạo hàm mới nhất lớp 11, 12 [Bản đầy đủ 2023]

Trong quá trình học Toán, chắc hẳn các bạn học sinh cấp 3 không thể không đụng đến kiến thức về đạo hàm. Kiến thức này không chỉ quan trọng trong các cuộc thi tốt nghiệp hay thi đại học mà còn có ảnh hưởng trong quá trình học đại học. Để giúp các bạn ôn lại kiến thức này một cách đơn giản và dễ hiểu, hãy cùng trường mầm non Sakura Montessori tham khảo tổng hợp các công thức mới nhất trong bài viết dưới đây.

Định nghĩa & quy tắc cơ bản

Công thức đạo hàm là một kiến thức quan trọng trong bài thi tốt nghiệp THPT quốc gia, do đó bất kỳ học sinh nào cũng cần phải nắm vững phần này. Tuy nhiên, nhiều người học cảm thấy khá khó hiểu. Để học tốt, chúng ta cần nắm vững lý thuyết, sau đó thực hành giải các bài tập để tiến đến thành thạo.

1. Định nghĩa

Đạo hàm là một hàm số, được sử dụng để mô tả sự biến thiên tại một điểm của hàm số. Nói cách khác, đạo hàm là tỉ số giữa số gia và hàm số tại một điểm x0. Trong đó, chiều biến thiên và độ lớn của biến thiên thể hiện giá trị của đạo hàm.

Hàm số y = f(x) ký hiệu bằng y'(x0) hoặc f'(x0) được xác định trên khoảng (a;b) và x0 ∈ (a;b).

Đạo hàm của hàm số f(x) tại x0 là giới hạn hữu hạn của tỉ số giữa số gia của đối số và số gia của hàm số.

Số gia của đối số là Δx = x – x0.

Số gia của hàm số là Δy = y – y0.

Lưu ý: Đạo hàm có ý nghĩa lớn trong ứng dụng hình học, hình học không gian và vật lý. Trong vật lý, y'(x0) là vận tốc tức thời, vận tốc tại thời điểm tính trong quá trình chuyển động của một chất. Hay nó chính là đồ thị biểu diễn hàm số biểu diễn hình học.

2. Quy tắc cơ bản để áp dụng công thức đạo hàm lớp 11

Quy tắc cơ bản để áp dụng công thức đạo hàm lớp 11 chính là công thức tính y’ đầy đủ giúp chúng ta tính toán và giải các bài tập một cách chính xác và nhanh chóng. Công thức này được sử dụng như sau:

Xem thêm: IELTS là gì? Cập nhật mới nhất 2023 kỳ thi IELTS – Sakura Montessori

Công thức Đạo hàm tổng quan

Công thức Đạo hàm tổng quan bao gồm 3 dạng: Đạo hàm của f(u) với u là hàm số, (f(x))’ với x là biến số và đạo hàm của một số phân thức hữu tỉ.

Xem thêm : Cách Vẽ Hình Trong Scratch

Xem thêm: Nguyên tử khối là gì? Cập nhật bảng nguyên tử khối mới nhất 2023

Công thức Đạo hàm sơ cấp

Công thức Đạo hàm sơ cấp:

Công thức Đạo hàm cấp cao

Công thức Đạo hàm cấp cao:

Công thức Đạo hàm lượng giác

Công thức Đạo hàm lượng giác:

Bảng công thức Đạo hàm mới nhất 2023

Bảng công thức mới nhất 2023:

Các dạng bài tập liên quan

Để giúp các em học sinh nắm bắt và hiểu rõ các công thức đạo hàm và ứng dụng như thế nào, chúng tôi đưa ra tổng hợp các dạng bài tập liên quan có kèm theo ví dụ dưới đây. Tích cực luyện tập bài tập sẽ giúp các em ghi nhớ kiến thức và giải bài tập thành thạo.

Dạng 1: Dạng bài tập đạo hàm áp dụng khái niệm, định nghĩa đạo hàm

Áp dụng khái niệm và định nghĩa giải các bài tập liên quan là dạng bài toán cơ bản và đơn giản. Cụ thể:

Dạng 2: Viết phương trình tiếp tuyến của hàm số căn cứ và tiếp điểm

Đây là dạng bài tập cơ bản khá phổ biến, đề bài cho sẵn tiếp điểm M(x0, y0), phương trình tiếp tuyến của hàm số của đồ thị (C): y = f(x), có dạng y = y’(x0)(x – x0) + y0. Đây là dạng bài tập có lời giải đơn giản, học sinh chỉ cần thay thế các dữ liệu cho sẵn và tính toán để được đáp án chính xác.

Ví dụ:
Cho một hàm số y = x^3 + 3mx^2 + (m+1)x + 1 (1), trong đó m là một tham số thực. Hãy tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số tại điểm có hoành độ x = -1 và đi qua điểm A(1;2).

Đáp án:
TXD: Δ = R
y’ = f'(x) = 3x^2 + 6mx + m + 1
Với x0 = -1 => y0 = 2m – 1, f'(-1) = -5m + 4
Phương trình tiếp tuyến tại M(-1; 2m – 1): y = (-5m + 4)(x+1) + 2m – 1 (d)
Ta có A (1;2) ∈ (d) <=> (-5m + 4)2 + 2m – 1 = 2 => m = 5/8

Dạng 3: Chứng minh đẳng thức dựa vào điều kiện liên quan đến đạo hàm có sẵn

Dạng bài tập này yêu cầu học sinh tính toán và chứng minh các đẳng thức dựa vào các điều kiện có sẵn liên quan đến đạo hàm. Cụ thể:

Dạng 4: Phương trình và bất phương trình

Xem thêm : Tổng Hợp Bài Tập Incoterms 2010 Và Incoterms 2020 Có Đáp Án

Để tìm được kết quả chính xác của dạng toán này, học sinh cần kết hợp nhiều công thức đạo hàm và nguyên hàm để giải phương trình hay bất phương trình đã cho.

Dạng 5: Cho hệ số góc, viết phương trình tiếp

Dạng bài tập này cho biết Δ có hệ số góc là k, yêu cầu viết phương trình tiếp tuyến Δ của (C) : y = f(x).

Gọi M(x0 ; y0) là tiếp điểm. Tính y’ => y'(x0)

Phương trình tiếp tuyến Δ có hệ số góc k => y’ = (x0) = k (i)

x0 => y0 = f(x0) => Δ : y = k (x – x0) + y0

Lưu ý: Hệ số góc k = y'(x0) của tiếp tuyến Δ thường cho kiểu gián tiếp như sau:

Ví dụ:
Cho hàm số y = x^3 + 3 × 2 – 9x + 5 ( C). Tìm tiếp tuyến có hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của đồ thị (C ).

Đáp án:
Ta có y’ = f'( x ) = 3×2 + 6x – 9
Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, vậy f'( x0) = 3 x0^2 + 6 x0 – 9
Ta có 3 x0^2 + 6×0 – 9 = 3 ( x0^2+ 2×0 +1) – 12 = 3 (x0+1)^2- 12 > – 12
Vậy min f( x0)= – 12 tại x0= -1 => y0=16
=> Phương trình tiếp tuyến cần tìm: y = -12( x+1) + 16

Dạng 6: Áp dụng công thức đạo hàm, nguyên hàm giải bài tập

Muốn giải được bài tập dạng 6, học sinh cần nắm vững công thức y’ lớp 11 đã được học. Trong quá trình thực hiện, các em cần lưu ý rút gọn hàm số sau đó mới tiến hành tìm y’ của hàm số đó.

Dạng 7: Tính đạo hàm cấp cao (thông thường từ cấp 2 trở lên)

Muốn tính y’ cấp cao, học sinh cần nắm vững và áp dụng công thức tính từ cấp 2 hoặc công thức y(n) = (y(n-1))’. Lưu ý: Để tính y’ cấp n, các em cần thực hiện tính y’ từ cấp 1, 2, 3… để tìm ra công thức tính y’ cấp n.

Một số câu hỏi thường gặp

1. Cách ghi nhớ bảng đạo hàm hiệu quả?

Nhiều học sinh gặp khó khăn trong việc ghi nhớ bảng công thức. Đây là công thức khó nhớ, mang tính đặc thù của chuyên ngành toán học nên việc học thuộc không đơn giản. Dưới đây là một số cách ghi nhớ các công thức tính dễ nhớ, ghi nhớ lâu:

• Học tập nghiêm túc: Cần duy trì thái độ học tập nghiêm túc, tập trung và kiên trì tìm hiểu, hiểu rõ kiến thức mới để tiến bộ và đạt kết quả tốt.
• Trao đổi thông tin với bạn bè và giáo viên: Trao đổi với bạn bè và giáo viên để tìm ra lời giải đáp đúng đắn. Tìm kiếm thông tin, học hỏi, giao lưu trên các câu lạc bộ toán học, hội nhóm, diễn đàn.
• Luyện tập các dạng bài tập: Luyện tập nhiều dạng bài tập để ghi nhớ và tự tin giải các đề thi.
• Tìm tòi, nghiên cứu mở rộng kiến thức: Tìm ra các phương pháp giải bài tập mới và sáng tạo.

2. Cách giải bài tập đạo hàm nhanh nhất?

Muốn giải bài tập nhanh chóng, cần chú ý:

• Nắm vững kiến thức lý thuyết về đạo hàm.
• Vận dụng kiến thức lý thuyết vào giải các dạng bài tập đạo hàm.
• Thực hành làm đa dạng các bài tập để trở nên thành thạo.
• Tìm tòi, nghiên cứu mở rộng kiến thức để tìm ra các phương pháp giải bài tập sáng tạo.

3. Công cụ tính đạo hàm online?

Các công cụ tính đạo hàm online có thể tìm kiếm trên các website uy tín. Dưới đây là 5 website tính đạo hàm chính xác nhất và hoàn toàn miễn phí để tham khảo:

• banhoituidap.com: Website có hiển thị lời giải chi tiết, đồ thị mô tả hàm số đạo hàm trong thời gian nhanh chóng.
• mathpapa.com: Website hỗ trợ người dùng tính đạo hàm online nhanh chóng và chính xác.
• wolfamalpha.com: Website tính đạo hàm chính xác và hỗ trợ hiển thị đồ thị.
• Mathway: Website cung cấp công cụ tính đạo hàm online miễn phí.
• symbolab.com: Website quen thuộc và phổ biến, giải đáp hầu hết các bài toán liên quan đến đạo hàm.

Đạo hàm là một phần kiến thức quan trọng trong Toán học. Dù khó nhớ và khá khó áp dụng, nhưng lại xuất hiện trong nhiều kỳ thi quan trọng của học sinh. Vì vậy, học tập nghiêm túc, hiểu sâu và rèn luyện các dạng bài tập đa dạng là rất cần thiết. Nếu còn gặp khó khăn, hãy tìm sự hỗ trợ từ giáo viên hoặc liên hệ với chúng tôi. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới.

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập