Bạn có biết rằng việc tính toán nguyên hàm từng phần là một trong những phương pháp giải các dạng bài toán liên quan đến nguyên hàm? Trong bài viết này, chúng ta sẽ tìm hiểu về khái niệm nguyên hàm từng phần, các công thức cơ bản và cách giải bài tập.
Contents
1. Lý thuyết nguyên hàm từng phần
1.1. Khái niệm nguyên hàm từng phần
Nguyên hàm từng phần là phương pháp giải các dạng bài toán liên quan đến nguyên hàm. Khi cho hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên một khoảng K, chúng ta có công thức nguyên hàm từng phần là ∫udv = uv – ∫vdu.
Bạn đang xem: Công thức tính nguyên hàm từng phần và cách giải bài tập
Đáng chú ý là phương pháp này được áp dụng khi nguyên hàm có dạng I = ∫f(x).g(x)dx, trong đó f(x) và g(x) là hai trong số bốn hàm số: hàm số logarit, hàm số lượng giác, hàm số đa thức, và hàm số mũ.
1.2. Ví dụ về nguyên hàm từng phần
Hãy xem các ví dụ sau để hiểu rõ hơn về nguyên hàm từng phần:
Ví dụ 1: Tìm nguyên hàm của hàm số x.sinx
Để tính nguyên hàm của hàm số trên, ta có:
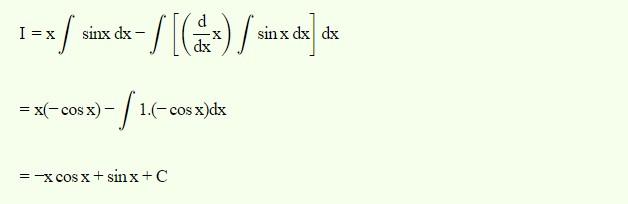
Ví dụ 2: Tìm nguyên hàm của hàm số ?
Giải:

Ví dụ 3: Tìm nguyên hàm của hàm số y = x.lnx
Giải:

.png)
2. Tổng hợp các công thức tính nguyên hàm từng phần
Cho hai hàm số u = u(x) và v = v(x) có đạo hàm trên một khoảng K, ta có công thức tính nguyên hàm từng phần như sau:
Để tính nguyên hàm ∫f(x).g(x)dx, chúng ta làm theo công thức sau:
Bước 1: Đặt:
Theo đó, G(x) là một nguyên hàm bất kỳ của hàm số g(x).
Bước 2: Theo công thức nguyên hàm từng phần, ta có:
Xem thêm : Abstract class và Interface trong Java
∫f(x).g(x)dx = f(x).G(x) – ∫G(x).f'(x)dx.
Lưu ý: Khi I = ∫f(x).g(x)dx và f(x) và g(x) là hai trong số bốn hàm số: hàm số logarit, hàm số đa thức, hàm số lượng giác, và hàm số mũ, ta đặt theo quy tắc đặt u.
Các bạn học sinh có thể nhớ cách đặt ẩn theo câu sau:
“Nhất log (bao gồm các hàm log, ln) – Nhì đa (tức là các hàm đa thức)
Tam lượng (tức là các hàm lượng giác) – Tứ mũ ( tức là các hàm mũ)”
Câu trên giúp chúng ta xác định thứ tự đặt ẩn cho từng hàm số. Ví dụ:
-
Trong trường hợp f(x) là hàm log và g(x) là một trong ba hàm số còn lại, ta đặt:
-
Tương tự, trong trường hợp f(x) là hàm mũ và g(x) là hàm đa thức, ta đặt:
3. Phương pháp giải nguyên hàm từng phần
Dưới đây là các phương pháp giải các dạng bài tập nguyên hàm từng phần:
Dạng 1: Tìm nguyên hàm của hàm số logarit
Hãy tính nguyên hàm của hàm số logarit sau:
Với f(x) là một hàm của đa thức.
Phương pháp giải:
-
Bước 1: Đặt:
-
Bước 2: Sau khi làm xong bước 1 ta biến đổi hàm số về dạng:
Dạng 2: Tìm nguyên hàm của hàm số mũ
Hãy tính nguyên hàm của hàm số mũ sau:
Xem thêm : End To End là gì? Vai trò và đặc điểm của quy trình đầu cuối | TIGODOO – Chuyển đổi số doanh nghiệp
Với f(x) là một hàm đa thức.
Phương pháp:
-
Bước 1: Đặt:
-
Bước 2: Dựa vào bước đặt ở bước 1, ta có: ∫f(x)e^ax+b dx = uv – ∫vdu.
Dạng 3: Tính nguyên hàm của hàm số lượng giác và hàm đa thức
Hãy tính nguyên hàm của hàm số lượng giác hoặc hàm số đa thức sau:
Lời giải:
-
Bước 1: Đặt như sau:
-
Bước 2: Ta biến đổi thành:
Dạng 4: Tính nguyên hàm kết hợp giữa hàm số lượng giác và hàm số mũ
Hãy tính nguyên hàm kết hợp giữa hàm số lượng giác và hàm số mũ sau:
hoặc
Các bước giải như sau:
-
Bước 1: Đặt như sau:
-
Bước 2: Khi đó, nguyên hàm sẽ tính theo công thức tổng quát uv – ∫vdu.
Lưu ý: Đây là dạng toán phức tạp, nên cần lấy nguyên hàm từng phần 2 lần. Ngoài ra, ở bước 1 ta có thể đặt khác như sau:
Trên đây là những kiến thức cơ bản và các phương pháp giải nguyên hàm từng phần mà chúng ta cần biết. Hy vọng rằng bài viết này đã giúp các bạn hiểu rõ hơn về công thức tính nguyên hàm từng phần và cách giải các bài tập liên quan. Đừng quên thực hành nhiều bài tập để nắm vững kiến thức này nhé!
Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập