Cây nhị phân tìm kiếm là một cấu trúc dữ liệu thường được sử dụng trong lĩnh vực tin học. Nó giúp tìm kiếm, thêm và xóa các phần tử một cách nhanh chóng và hiệu quả. Bài viết này sẽ giới thiệu về cây nhị phân tìm kiếm và cách cài đặt một cây đơn giản.
Contents
Cây nhị phân tìm kiếm là gì?
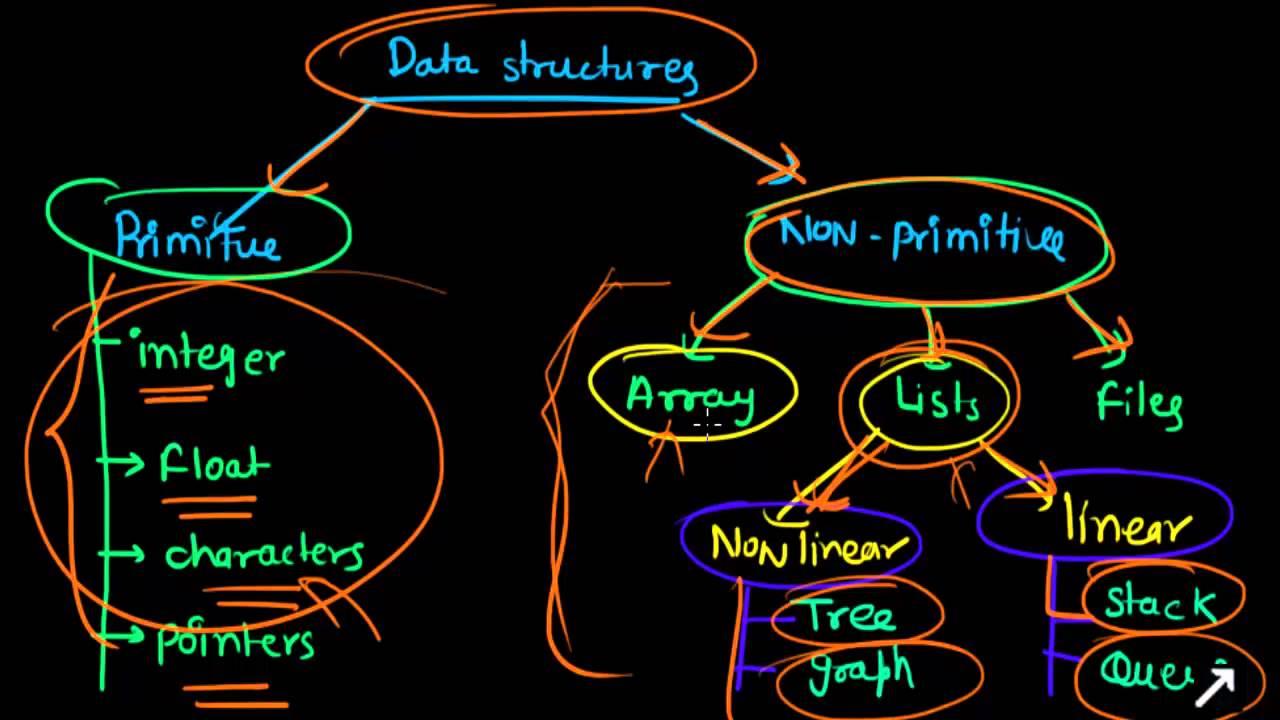
Cây nhị phân tìm kiếm là một cấu trúc dữ liệu gồm nhiều nút, mỗi nút có tối đa 2 nút con: nút con trái và nút con phải. Các nút không có nút con nào được gọi là nút lá. Mỗi nút có một khóa duy nhất để lưu trữ thông tin. Các nút trong cây phải thỏa mãn một số tính chất:
Bạn đang xem: Sơ lược về cây nhị phân
- Khóa của các đỉnh không trùng lặp.
- Với mỗi đỉnh, khóa của tất cả các đỉnh trong cây con bên trái nhỏ hơn.
- Với mỗi đỉnh, khóa của tất cả các đỉnh trong cây con bên phải lớn hơn.
.png)
Cài đặt cây nhị phân tìm kiếm
Trong C++, cây nhị phân tìm kiếm được cài đặt bằng cách sử dụng con trỏ. Mỗi nút của cây có ba thuộc tính: con trái, con phải và khóa. Ta có thể thêm một nút mới vào cây thông qua việc thêm các khóa và cải tiến cây nhị phân.
Thêm một nút vào cây
Việc thêm một nút mới vào cây được thực hiện theo quy trình đệ quy. Nếu vị trí đang xét chưa tồn tại nút nào, ta tạo một nút mới với khóa cần thêm. Nếu nút đang xét đã tồn tại, ta kiểm tra và đẩy nút con mới vào cây con bên trái hoặc bên phải, tùy thuộc vào kết quả so sánh.
Tìm kiếm một nút trong cây
Thao tác tìm kiếm cũng được thực hiện theo quy trình đệ quy. Nếu vị trí đang xét không có nút, ta trả về NULL. Ngược lại, ta so sánh khóa cần tìm với khóa của nút đang xét và di chuyển sang cây con bên trái hoặc bên phải hoặc trả về nút hiện tại tùy thuộc vào kết quả so sánh.
Xóa một nút trong cây
Xem thêm : Ngày cấp chứng chỉ IELTS ghi ở đâu? Và cách đăng ký thi IELTS
Việc xóa một nút khá phức tạp hơn so với việc thêm và tìm kiếm. Tùy thuộc vào số lượng nút con của nút cần xóa, ta có các trường hợp xử lý khác nhau.
Cài đặt trong C++
Cài đặt cây nhị phân tìm kiếm trong C++ được thực hiện bằng cách sử dụng các phương thức và cấu trúc dữ liệu. Việc gọi các phương thức cùng với gán nút gốc giúp thực hiện các thao tác trên cây. Độ phức tạp của các thao tác trên cây nhị phân tìm kiếm tùy thuộc vào độ cao của cây khi truy vấn. Với dữ liệu ngẫu nhiên, cách cài đặt này có độ phức tạp trung bình là O(log N), với N là số nút trên cây. Tuy nhiên, độ phức tạp trong trường hợp xấu nhất là O(N), nên cách cài đặt này không phù hợp cho thực tế.
Ảnh:
(Ảnh minh hoạ cho cây nhị phân)
Ảnh:
(Ví dụ cây nhị phân tìm kiếm với khóa là số nguyên)
Trên đây là sơ lược về cây nhị phân tìm kiếm và cách cài đặt một cây nhị phân đơn giản. Hy vọng bài viết này giúp bạn hiểu rõ hơn về cấu trúc và quy trình làm việc của cây nhị phân tìm kiếm.
Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập