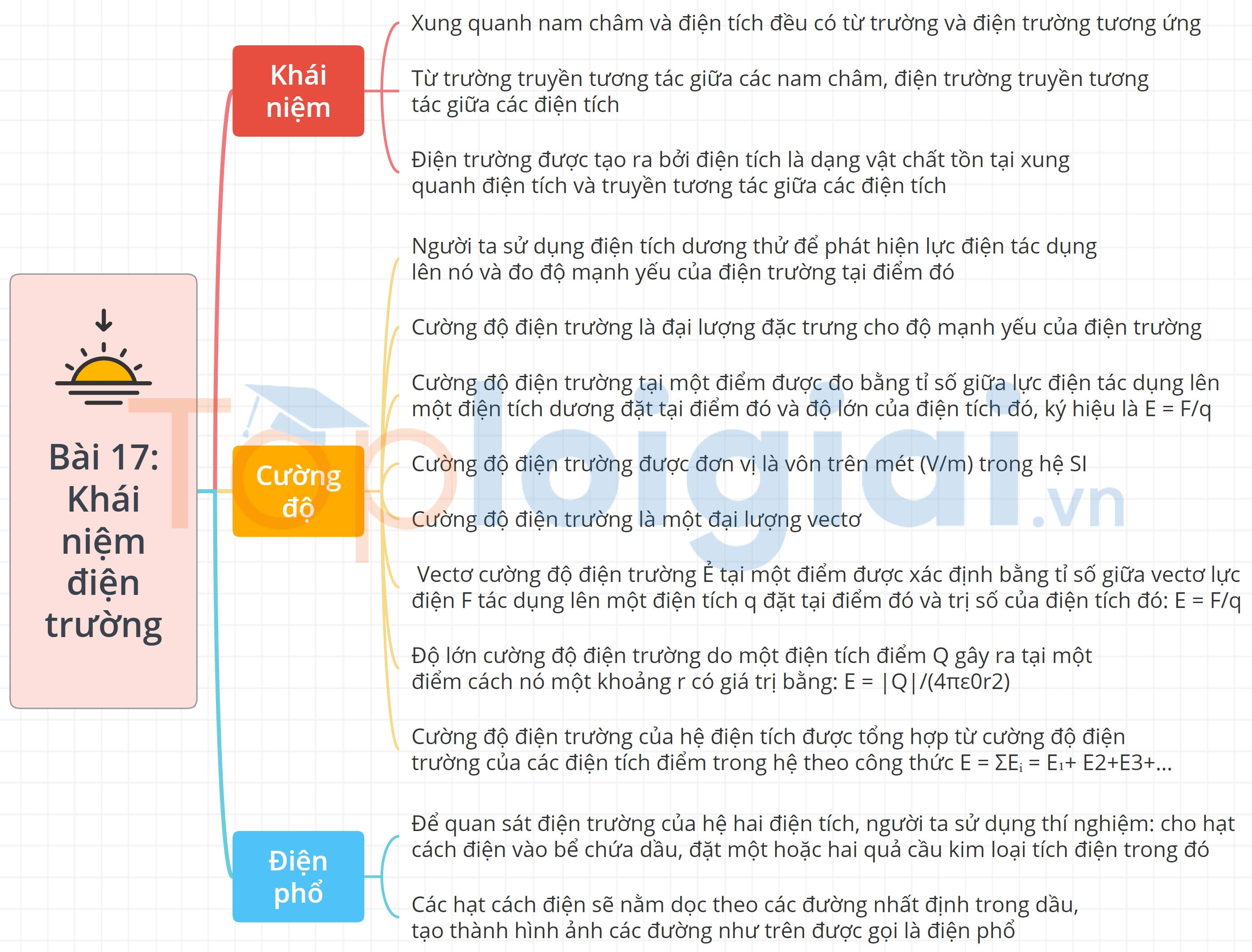
Chủ đề xác định cường độ điện trường: Xác định cường độ điện trường là một chủ đề quan trọng trong vật lý, giúp hiểu rõ về cách lực điện tác dụng lên các điện tích. Bài viết này sẽ hướng dẫn chi tiết các phương pháp tính toán cường độ điện trường và giới thiệu những ứng dụng thực tế trong cuộc sống hiện đại.
Mục lục
Cách xác định cường độ điện trường
Cường độ điện trường là đại lượng đặc trưng cho độ mạnh của điện trường tại một điểm và được xác định bằng thương số giữa lực điện \( \vec{F} \) tác dụng lên một điện tích thử \( q \) và độ lớn của \( q \).
Công thức xác định cường độ điện trường:
\[ \vec{E} = \frac{\vec{F}}{q} \]
Trong đó:
- \( \vec{E} \): Cường độ điện trường (V/m)
- \( \vec{F} \): Lực điện tác dụng lên điện tích thử \( q \) (N)
- \( q \): Điện tích thử (C)
Phương pháp xác định cường độ điện trường
- Bước 1: Xác định lực điện \( \vec{F} \) tác dụng lên điện tích thử \( q \).
- Bước 2: Sử dụng công thức \( \vec{E} = \frac{\vec{F}}{q} \) để tính cường độ điện trường.
- Bước 3: Xác định phương và chiều của véc tơ \( \vec{E} \) trùng với phương và chiều của lực điện \( \vec{F} \).
Công thức cường độ điện trường của điện tích điểm
Đối với điện tích điểm \( Q \), cường độ điện trường tại một điểm cách điện tích một khoảng \( r \) trong chân không được tính bằng công thức:
\[ E = k \cdot \frac{|Q|}{r^2} \]
Trong đó:
- \( k \): Hằng số điện môi (\( 9 \times 10^9 \, \text{N.m}^2/\text{C}^2 \))
- \( Q \): Điện tích tạo ra điện trường (C)
- \( r \): Khoảng cách từ điện tích đến điểm cần xét (m)
Nguyên lý chồng chất điện trường
Nếu có nhiều điện tích tạo ra điện trường tại một điểm, cường độ điện trường tổng hợp tại điểm đó là tổng của các véc tơ cường độ điện trường do từng điện tích gây ra. Công thức tổng hợp cường độ điện trường:
\[ \vec{E}_{\text{tổng}} = \vec{E}_1 + \vec{E}_2 + ... + \vec{E}_n \]
Ứng dụng của cường độ điện trường
- Xác định lực điện tác dụng lên các điện tích thử trong điện trường.
- Giải quyết các bài toán liên quan đến điện trường và điện tích trong vật lý.
- Ứng dụng trong các thiết bị điện tử, cảm biến và công nghệ truyền dẫn điện năng.
.png)
Giới thiệu về cường độ điện trường
Cường độ điện trường là một đại lượng vật lý đặc trưng cho khả năng tác dụng lực của điện trường tại một điểm trong không gian. Nó mô tả sự ảnh hưởng của điện trường lên một điện tích thử được đặt tại điểm đó, với giá trị và hướng cụ thể.
Về cơ bản, cường độ điện trường được xác định bằng công thức:
\[ \vec{E} = \frac{\vec{F}}{q} \]
Trong đó:
- \( \vec{E} \): Cường độ điện trường (V/m).
- \( \vec{F} \): Lực điện tác dụng lên điện tích thử (N).
- \( q \): Điện tích thử (C).
Các bước để xác định cường độ điện trường:
- Xác định lực điện \( \vec{F} \) tác dụng lên điện tích thử \( q \).
- Tính toán giá trị cường độ điện trường \( \vec{E} \) bằng cách áp dụng công thức \( \vec{E} = \frac{\vec{F}}{q} \).
- Xác định phương và chiều của véc tơ \( \vec{E} \), luôn cùng phương với lực \( \vec{F} \).
Cường độ điện trường tại một điểm phụ thuộc vào:
- Giá trị của điện tích gây ra điện trường.
- Khoảng cách từ điện tích đến điểm xét.
Trong trường hợp của một điện tích điểm, công thức cường độ điện trường được tính như sau:
\[ E = k \cdot \frac{|Q|}{r^2} \]
Trong đó:
- \( k \): Hằng số điện môi (xấp xỉ \( 9 \times 10^9 \, \text{N.m}^2/\text{C}^2 \)).
- \( Q \): Điện tích gây ra điện trường (C).
- \( r \): Khoảng cách từ điện tích đến điểm xét (m).
Công thức xác định cường độ điện trường
Cường độ điện trường tại một điểm được xác định thông qua lực điện tác dụng lên một điện tích thử đặt tại điểm đó. Công thức tổng quát để xác định cường độ điện trường là:
\[ \vec{E} = \frac{\vec{F}}{q} \]
Trong đó:
- \( \vec{E} \): Cường độ điện trường (V/m).
- \( \vec{F} \): Lực điện tác dụng lên điện tích thử (N).
- \( q \): Điện tích thử (C).
Để tính toán cường độ điện trường của một điện tích điểm \( Q \), công thức cụ thể là:
\[ E = k \cdot \frac{|Q|}{r^2} \]
Trong đó:
- \( k \): Hằng số điện môi (\( k \approx 9 \times 10^9 \, \text{N.m}^2/\text{C}^2 \)).
- \( Q \): Điện tích gây ra điện trường (C).
- \( r \): Khoảng cách từ điện tích đến điểm cần xét (m).
Các bước để tính toán cường độ điện trường:
- Xác định điện tích gây ra điện trường \( Q \).
- Xác định khoảng cách \( r \) từ điện tích đến điểm xét.
- Áp dụng công thức \( E = k \cdot \frac{|Q|}{r^2} \) để tính cường độ điện trường tại điểm đó.
Ví dụ: Nếu điện tích \( Q \) là \( 5 \, \text{C} \) và khoảng cách \( r \) là \( 2 \, \text{m} \), cường độ điện trường tại điểm cách điện tích \( Q \) một khoảng \( r \) sẽ được tính như sau:
\[ E = 9 \times 10^9 \cdot \frac{5}{2^2} = 1.125 \times 10^{10} \, \text{V/m} \]
Như vậy, cường độ điện trường tại điểm xét là \( 1.125 \times 10^{10} \, \text{V/m} \).

Các yếu tố ảnh hưởng đến cường độ điện trường
Cường độ điện trường tại một điểm trong không gian bị ảnh hưởng bởi nhiều yếu tố, mỗi yếu tố có tác động trực tiếp đến độ lớn và hướng của cường độ điện trường. Dưới đây là các yếu tố chính:
- 1. Điện tích nguồn
- 2. Khoảng cách từ điện tích đến điểm xét
- 3. Môi trường xung quanh
Cường độ điện trường phụ thuộc trực tiếp vào giá trị của điện tích tạo ra điện trường. Điện tích càng lớn thì cường độ điện trường càng mạnh. Theo công thức:
\[ E = k \cdot \frac{|Q|}{r^2} \]
Trong đó \( Q \) là điện tích nguồn. Khi giá trị của \( Q \) tăng, cường độ điện trường \( E \) tại khoảng cách \( r \) không đổi sẽ tăng lên tương ứng.
Cường độ điện trường giảm theo bình phương khoảng cách từ điện tích đến điểm xét. Khoảng cách càng lớn, cường độ điện trường càng giảm. Theo công thức:
\[ E = k \cdot \frac{|Q|}{r^2} \]
Điều này có nghĩa là nếu khoảng cách tăng lên gấp đôi, cường độ điện trường sẽ giảm đi bốn lần.
Môi trường mà điện tích tồn tại cũng ảnh hưởng đến cường độ điện trường. Điện trường sẽ bị yếu đi trong môi trường có hằng số điện môi \( \varepsilon \) lớn hơn. Trong chân không, hằng số điện môi là nhỏ nhất, dẫn đến cường độ điện trường lớn hơn so với trong môi trường chất lỏng hoặc chất rắn.
Công thức tổng quát trong môi trường có hằng số điện môi là:
\[ E = \frac{1}{4 \pi \varepsilon} \cdot \frac{|Q|}{r^2} \]
Trong đó \( \varepsilon \) là hằng số điện môi của môi trường.
Các yếu tố trên đều cần được xem xét khi tính toán và dự đoán cường độ điện trường tại một điểm bất kỳ trong không gian.