Chủ đề độ lớn cường độ điện trường: Độ lớn cường độ điện trường là một khái niệm quan trọng trong vật lý, ảnh hưởng đến nhiều lĩnh vực từ nghiên cứu khoa học đến ứng dụng kỹ thuật. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm, cách tính toán cũng như ứng dụng của cường độ điện trường trong đời sống và công nghiệp.
Mục lục
Độ Lớn Cường Độ Điện Trường
Cường độ điện trường là một đại lượng vật lý đặc trưng cho tác dụng lực của điện trường lên các điện tích trong không gian xung quanh nó. Đây là một khái niệm quan trọng trong lĩnh vực vật lý và kỹ thuật điện, đóng vai trò quan trọng trong việc thiết kế và đánh giá các hệ thống điện. Cường độ điện trường tại một điểm trong không gian được xác định bằng tỉ số giữa lực điện \( \vec{F} \) tác dụng lên một điện tích thử \( q \) đặt tại điểm đó và độ lớn của điện tích thử.
Công Thức Cường Độ Điện Trường
Công thức tính cường độ điện trường \( E \) tại một điểm được cho bởi:
\[
E = \frac{F}{q}
\]
Trong đó:
- \( E \) là cường độ điện trường tại điểm xét (đơn vị: V/m).
- \( F \) là độ lớn của lực tác dụng lên điện tích thử tại điểm đó (đơn vị: Newton, N).
- \( q \) là độ lớn của điện tích thử (đơn vị: Coulomb, C).
Vectơ Cường Độ Điện Trường
Cường độ điện trường là một đại lượng vectơ, nghĩa là nó có cả độ lớn và hướng. Vectơ cường độ điện trường \( \vec{E} \) có phương và chiều trùng với phương và chiều của lực điện \( \vec{F} \) tác dụng lên điện tích thử \( q \). Chiều dài của vectơ \( \vec{E} \) biểu diễn độ lớn của cường độ điện trường.
Độ Lớn Cường Độ Điện Trường Do Điện Tích Điểm Gây Ra
Cường độ điện trường tại một điểm do một điện tích điểm \( Q \) sinh ra được xác định bằng công thức:
\[
E = k \cdot \frac{|Q|}{r^2}
\]
Trong đó:
- \( k \) là hằng số điện trường \( k \approx 8.99 \times 10^9 \, \text{Nm}^2/\text{C}^2 \).
- \( Q \) là độ lớn của điện tích điểm (đơn vị: C).
- \( r \) là khoảng cách từ điện tích điểm đến điểm xét (đơn vị: m).
Ứng Dụng Của Cường Độ Điện Trường
Cường độ điện trường có vai trò quan trọng trong nhiều lĩnh vực, đặc biệt là trong thiết kế và phân tích các hệ thống điện. Nó giúp các kỹ sư đảm bảo an toàn và hiệu quả hoạt động của các thiết bị điện, đồng thời cũng là một yếu tố cơ bản trong việc nghiên cứu và hiểu rõ các hiện tượng điện từ.
| Lĩnh vực ứng dụng | Mô tả |
| Thiết kế hệ thống điện | Cường độ điện trường được sử dụng để tính toán, đảm bảo an toàn cho các thiết bị và hệ thống điện. |
| Nghiên cứu vật lý | Các nhà khoa học sử dụng cường độ điện trường để nghiên cứu và mô phỏng các hiện tượng điện từ. |
| Giáo dục | Cường độ điện trường là một chủ đề cơ bản trong các chương trình học vật lý và kỹ thuật điện. |
Cường độ điện trường là một khái niệm cơ bản và quan trọng, không chỉ trong lý thuyết mà còn trong ứng dụng thực tế, đóng góp vào sự phát triển của khoa học kỹ thuật và các ngành công nghiệp điện tử.

.png)
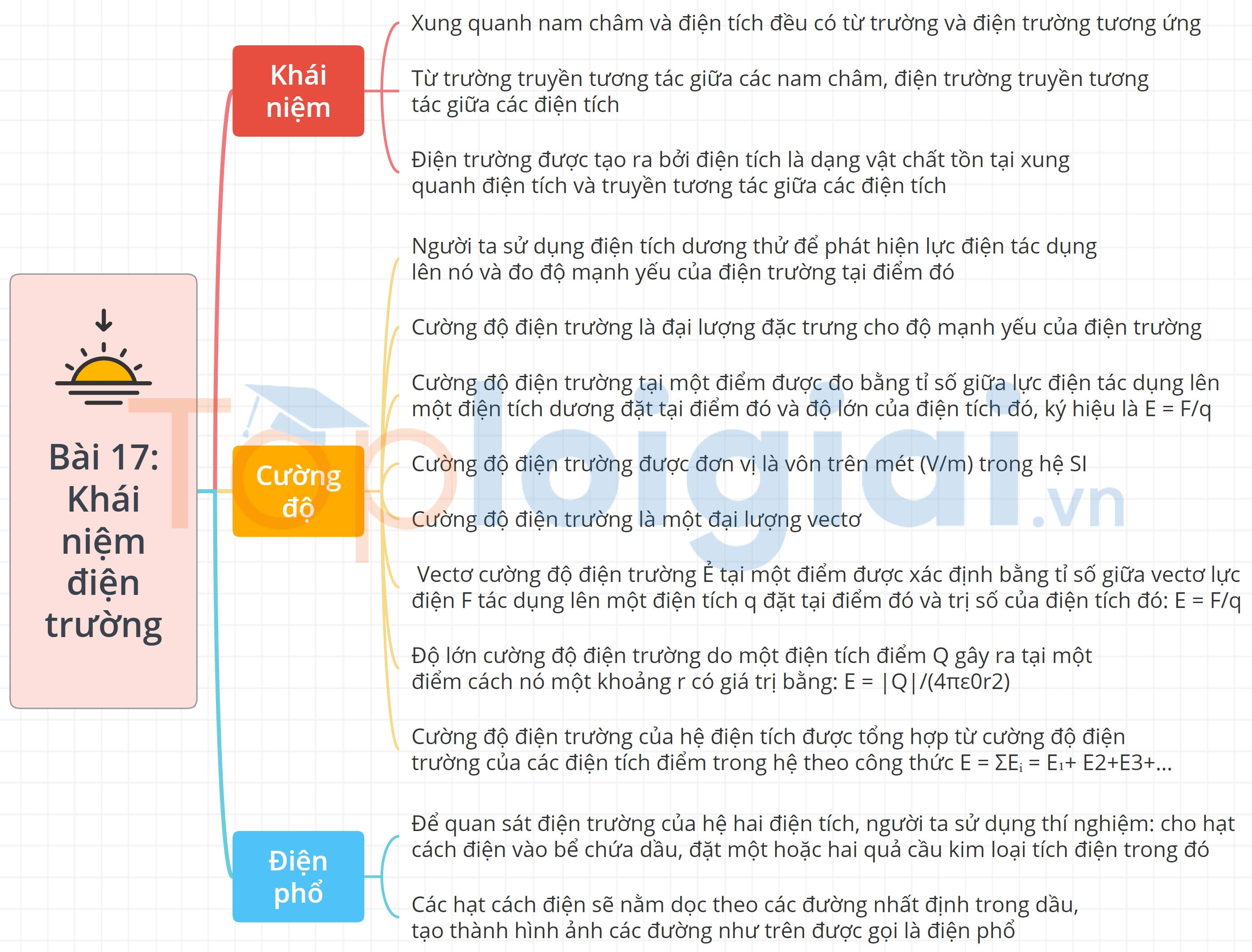
1. Khái niệm cường độ điện trường
Cường độ điện trường là một đại lượng vật lý quan trọng, mô tả độ mạnh yếu của điện trường tại một điểm nhất định trong không gian. Nó thể hiện lực tác dụng lên một điện tích đơn vị đặt tại điểm đó. Cường độ điện trường được ký hiệu là \( \vec{E} \) và được định nghĩa bằng công thức:
Trong đó:
- \(\vec{E}\): Cường độ điện trường (đơn vị: V/m).
- \(\vec{F}\): Lực điện tác dụng lên điện tích thử \(q\) (đơn vị: N).
- \(q\): Điện tích thử (đơn vị: C).
Điện trường là một dạng trường vô hình bao quanh các hạt mang điện, và cường độ điện trường mô tả lực mà điện trường đó tác động lên một điện tích thử. Một số đặc điểm chính của cường độ điện trường gồm:
- Cường độ điện trường tại một điểm luôn có phương và chiều giống với lực điện tác dụng lên điện tích dương đặt tại điểm đó.
- Độ lớn của cường độ điện trường tỉ lệ thuận với lực điện tác dụng và tỉ lệ nghịch với điện tích thử.
Cường độ điện trường có thể được tạo ra bởi các nguồn điện tích như điện tích điểm, dây dẫn điện tích, hay các hệ thống phân bố điện tích phức tạp. Tính chất và cách tính cường độ điện trường tùy thuộc vào hình dạng và phân bố của nguồn điện tích.
2. Công thức tính cường độ điện trường
Cường độ điện trường \( E \) tại một điểm trong không gian được xác định bởi lực \( F \) tác dụng lên một điện tích thử \( q \) đặt tại điểm đó. Công thức tổng quát để tính cường độ điện trường là:
\( E = \frac{F}{q} \)
Trong đó:
- \( E \): Cường độ điện trường (đơn vị V/m).
- \( F \): Lực điện tác dụng lên điện tích thử \( q \) (đơn vị N).
- \( q \): Điện tích thử (đơn vị C).
2.1 Công thức tổng quát
Trong trường hợp điện trường được tạo ra bởi một điện tích điểm \( Q \), cường độ điện trường tại khoảng cách \( r \) từ điện tích đó được tính theo công thức:
\( E = k \cdot \frac{|Q|}{r^2} \)
Trong đó:
- \( E \): Cường độ điện trường tại khoảng cách \( r \) (đơn vị V/m).
- \( k \): Hằng số Coulomb, \( k \approx 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \).
- \( Q \): Điện tích tạo ra điện trường (đơn vị C).
- \( r \): Khoảng cách từ điện tích điểm \( Q \) đến điểm cần xét (đơn vị m).
2.2 Công thức cho điện tích điểm
Cường độ điện trường của một điện tích điểm trong chân không được xác định bằng công thức:
\( E = \frac{k \cdot |Q|}{r^2} \)
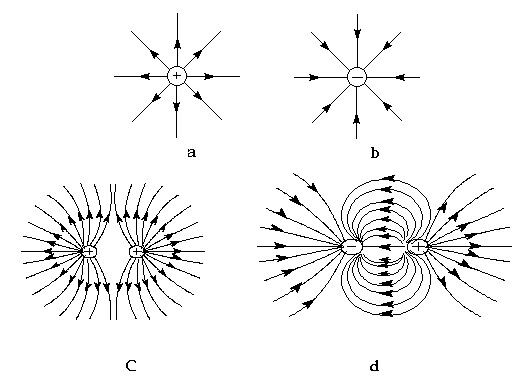
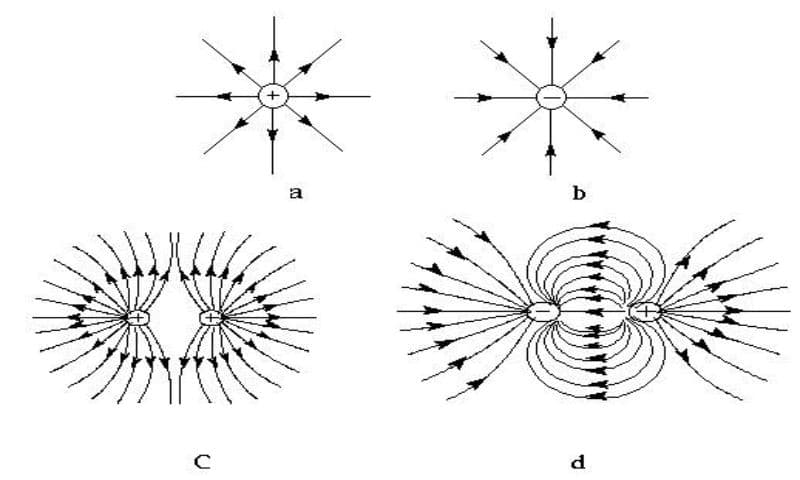
Điện trường do một điện tích điểm \( Q \) tạo ra sẽ có hướng phụ thuộc vào dấu của \( Q \). Nếu \( Q \) là điện tích dương, vectơ điện trường sẽ hướng ra xa \( Q \). Nếu \( Q \) là điện tích âm, vectơ sẽ hướng về phía \( Q \).
2.3 Công thức cho điện trường đồng nhất
Trong một điện trường đồng nhất, cường độ điện trường có cùng độ lớn và hướng tại mọi điểm trong không gian. Công thức tính cường độ điện trường đồng nhất là:
\( E = \frac{V}{d} \)
Trong đó:
- \( E \): Cường độ điện trường đồng nhất (đơn vị V/m).
- \( V \): Hiệu điện thế giữa hai bản cực (đơn vị V).
- \( d \): Khoảng cách giữa hai bản cực (đơn vị m).

3. Vectơ cường độ điện trường
Vectơ cường độ điện trường, ký hiệu là \(\overrightarrow{E}\), là một đại lượng vectơ thể hiện tác dụng lực của điện trường tại một điểm bất kỳ trong không gian. Vectơ này có các đặc điểm chính như sau:
- Phương và Chiều: Phương và chiều của vectơ cường độ điện trường trùng với phương và chiều của lực điện tác dụng lên điện tích thử dương. Nếu điện tích thử là dương, vectơ \(\overrightarrow{E}\) sẽ hướng ra xa điện tích nguồn; nếu điện tích thử là âm, vectơ \(\overrightarrow{E}\) sẽ hướng về phía điện tích nguồn.
- Độ Lớn: Độ lớn của vectơ cường độ điện trường được xác định theo công thức:
\[
E = \frac{F}{q}
\]
Trong đó:
- \(E\) là độ lớn cường độ điện trường.
- \(F\) là lực điện tác dụng lên điện tích thử \(q\).
- \(q\) là điện tích thử dương đặt tại điểm xét.
- Công Thức: Độ lớn của cường độ điện trường tại một điểm do một điện tích điểm \(Q\) gây ra được tính theo công thức:
\[
E = k \cdot \frac{|Q|}{r^2}
\]
Trong đó:
- \(k\) là hằng số điện môi trong môi trường xét.
- \(Q\) là độ lớn của điện tích nguồn.
- \(r\) là khoảng cách từ điện tích nguồn \(Q\) đến điểm xét.
- Đơn vị: Đơn vị đo cường độ điện trường trong hệ SI là Vôn trên mét (V/m).
- Nguyên Lý Chồng Chất Điện Trường: Nếu tại một điểm có nhiều điện trường do nhiều điện tích gây ra, cường độ điện trường tổng hợp tại điểm đó sẽ bằng tổng các vectơ cường độ điện trường của từng điện trường thành phần, theo quy tắc tổng hợp vectơ: \[ \overrightarrow{E}_{total} = \overrightarrow{E}_1 + \overrightarrow{E}_2 + ... + \overrightarrow{E}_n \]
Như vậy, vectơ cường độ điện trường là một đại lượng không chỉ có độ lớn mà còn có hướng, và nó là yếu tố quyết định sự tương tác giữa các điện tích trong điện trường.
4. Ứng dụng của cường độ điện trường
Cường độ điện trường là một khái niệm quan trọng trong vật lý, có nhiều ứng dụng thực tiễn trong cuộc sống và các ngành công nghiệp. Dưới đây là một số ứng dụng nổi bật của cường độ điện trường:
- Trong thiết kế và sản xuất thiết bị điện: Cường độ điện trường được sử dụng để tính toán và thiết kế các linh kiện điện tử như tụ điện, điện trở, và cuộn cảm, giúp xác định hiệu suất và an toàn của các thiết bị điện.
- Trong y học: Cường độ điện trường được ứng dụng trong các thiết bị y tế như máy x-quang, máy MRI, và các thiết bị điện sinh học. Những thiết bị này sử dụng nguyên lý điện trường để chẩn đoán và điều trị bệnh tật.
- Trong nghiên cứu khoa học: Cường độ điện trường đóng vai trò quan trọng trong các thí nghiệm vật lý hiện đại, đặc biệt là trong nghiên cứu về các hạt cơ bản và các hiện tượng lượng tử. Điện trường mạnh có thể được sử dụng để kiểm soát và thay đổi trạng thái của các hạt trong các thí nghiệm phức tạp.
- Trong công nghệ năng lượng: Cường độ điện trường được sử dụng trong các hệ thống năng lượng như điện mặt trời và điện gió. Việc hiểu và kiểm soát cường độ điện trường giúp tối ưu hóa quá trình thu thập và chuyển đổi năng lượng.
Các ứng dụng trên cho thấy tầm quan trọng của cường độ điện trường trong nhiều lĩnh vực khác nhau, từ công nghiệp đến y học và nghiên cứu khoa học. Việc nắm vững kiến thức về cường độ điện trường sẽ giúp ích rất nhiều trong việc phát triển và ứng dụng các công nghệ hiện đại.

5. Bài tập và ví dụ minh họa
Dưới đây là một số bài tập và ví dụ minh họa về cường độ điện trường để giúp bạn hiểu rõ hơn về khái niệm và cách tính toán.
-
Bài tập 1: Tại hai điểm A và B cách nhau 15 cm trong không khí có hai điện tích
\(q_1 = 12 \times 10^{-6} \, \text{C}\) và\(q_2 = 3 \times 10^{-6} \, \text{C}\) . Xác định độ lớn cường độ điện trường do hai điện tích này gây ra tại điểm C, biết\(AC = 20 \, \text{cm}\) và\(BC = 5 \, \text{cm}\) .Hướng dẫn giải:
- Xác định cường độ điện trường do điện tích
\(q_1\) gây ra tại điểm C:\[E_1 = k \cdot \frac{|q_1|}{r_{AC}^2} = 9 \times 10^9 \cdot \frac{12 \times 10^{-6}}{0,2^2} = 27 \times 10^5 \, \text{V/m}\] - Xác định cường độ điện trường do điện tích
\(q_2\) gây ra tại điểm C:\[E_2 = k \cdot \frac{|q_2|}{r_{BC}^2} = 9 \times 10^9 \cdot \frac{3 \times 10^{-6}}{0,05^2} = 108 \times 10^5 \, \text{V/m}\] - Vì
\(q_1\) mang điện tích âm và\(q_2\) mang điện tích dương, nên cường độ điện trường tổng hợp tại C là:\[E = |E_1 - E_2| = 108 \times 10^5 - 27 \times 10^5 = 81 \times 10^5 \, \text{V/m}\]
- Xác định cường độ điện trường do điện tích
-
Bài tập 2: Tại hai điểm A và B cách nhau 5 cm trong chân không, có hai điện tích
\(q_1 = 16 \times 10^{-8} \, \text{C}\) và\(q_2 = -9 \times 10^{-8} \, \text{C}\) . Tính cường độ điện trường tổng hợp tại điểm C cách A và B lần lượt là 4 cm và 3 cm.Hướng dẫn giải:
- Xác định cường độ điện trường do
\(q_1\) gây ra tại C:\[E_1 = k \cdot \frac{|q_1|}{r_{AC}^2} = 9 \times 10^9 \cdot \frac{16 \times 10^{-8}}{0,04^2} = 9 \times 10^5 \, \text{V/m}\] - Xác định cường độ điện trường do
\(q_2\) gây ra tại C:\[E_2 = k \cdot \frac{|q_2|}{r_{BC}^2} = 9 \times 10^9 \cdot \frac{9 \times 10^{-8}}{0,03^2} = 10 \times 10^5 \, \text{V/m}\] - Sử dụng định lý Pythagoras để tính cường độ điện trường tổng hợp:
\[E = \sqrt{E_1^2 + E_2^2} = \sqrt{(9 \times 10^5)^2 + (10 \times 10^5)^2} \, \text{V/m}\]
- Xác định cường độ điện trường do