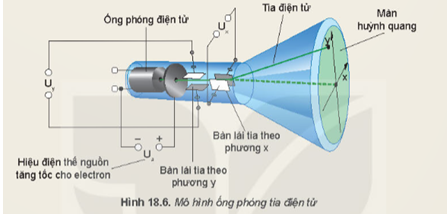
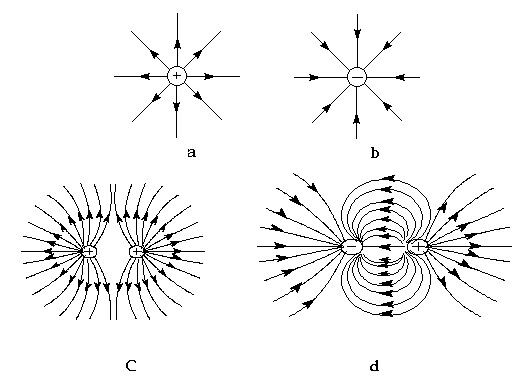
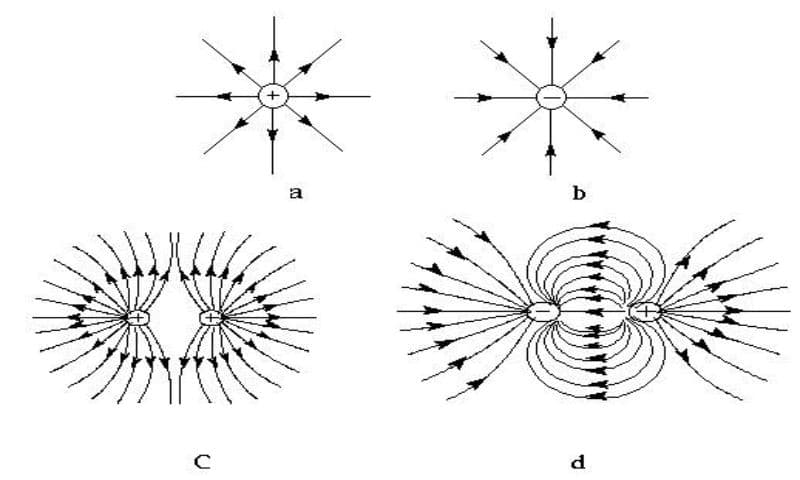
Chủ đề vecto cường độ điện trường và vecto cảm ứng từ: Khám phá toàn diện về vecto cường độ điện trường và vecto cảm ứng từ, từ khái niệm cơ bản đến công thức tính toán chi tiết. Bài viết cũng sẽ trình bày các ứng dụng thực tiễn của chúng trong cuộc sống hàng ngày và khoa học, giúp bạn hiểu rõ hơn về tầm quan trọng của hai đại lượng vật lý này.
Mục lục
Thông Tin Về Vecto Cường Độ Điện Trường và Vecto Cảm Ứng Từ
Các khái niệm "vecto cường độ điện trường" và "vecto cảm ứng từ" là những khái niệm cơ bản trong lĩnh vực Vật lý, đặc biệt là trong các bài học về Điện từ học. Dưới đây là thông tin chi tiết về hai khái niệm này.
Vecto Cường Độ Điện Trường
Vecto cường độ điện trường \(\vec{E}\) là đại lượng mô tả cường độ và hướng của điện trường tại một điểm cụ thể. Điện trường tạo ra lực điện tác dụng lên một điện tích thử đặt trong nó. Cường độ điện trường tại một điểm được định nghĩa là thương số giữa lực điện \(\vec{F}\) tác dụng lên điện tích thử \(q\) và độ lớn của điện tích đó:
\[
\vec{E} = \frac{\vec{F}}{q}
\]
- Phương và chiều: Vecto cường độ điện trường có phương và chiều trùng với phương và chiều của lực điện tác dụng lên điện tích thử dương.
- Độ lớn: Độ lớn của cường độ điện trường được đo bằng đơn vị V/m (vôn trên mét).
- Ứng dụng: Cường độ điện trường được sử dụng để phân tích tác dụng của điện trường lên các điện tích trong nhiều ứng dụng khoa học và công nghệ.
Vecto Cảm Ứng Từ
Vecto cảm ứng từ \(\vec{B}\) mô tả độ lớn và hướng của từ trường tại một điểm trong không gian. Từ trường có tác động lên các vật liệu dẫn điện và từ, tạo ra lực từ tác dụng lên các điện tích chuyển động.
Công thức tính cảm ứng từ do dòng điện thẳng dài gây ra tại một điểm cách dòng điện một khoảng \(r\) là:
\[
\vec{B} = \frac{\mu_0 I}{2 \pi r}
\]
- Trong đó:
- \( \mu_0 \) là hằng số từ trường trong chân không (khoảng 4π x 10-7 Tm/A).
- \( I \) là cường độ dòng điện chạy qua dây dẫn (A).
- \( r \) là khoảng cách từ điểm tính đến dây dẫn (m).
- Phương và chiều: Vecto cảm ứng từ có phương vuông góc với dây dẫn và hướng được xác định theo quy tắc bàn tay phải.
- Ứng dụng: Cảm ứng từ được sử dụng rộng rãi trong các thiết bị điện tử, máy phát điện, động cơ điện và nhiều ứng dụng khác liên quan đến từ trường.
Kết Luận
Cả vecto cường độ điện trường và vecto cảm ứng từ đều là những khái niệm cơ bản nhưng quan trọng trong vật lý. Chúng giúp chúng ta hiểu rõ hơn về các hiện tượng điện từ trường và các ứng dụng của chúng trong cuộc sống hàng ngày.
.png)
1. Khái Niệm Vecto Cường Độ Điện Trường và Vecto Cảm Ứng Từ
Vecto cường độ điện trường và vecto cảm ứng từ là hai khái niệm cơ bản trong vật lý học, đặc biệt là trong lĩnh vực điện từ trường. Chúng là đại lượng vector thể hiện tính chất và sức mạnh của các trường lực trong không gian.
- Vecto Cường Độ Điện Trường (\\(\overrightarrow{E}\\)):
Đại lượng này thể hiện sức mạnh và phương hướng của lực điện trường tác dụng lên một điện tích thử. Cường độ điện trường tại một điểm được xác định bằng công thức:
\\[
\overrightarrow{E} = \frac{\overrightarrow{F}}{q}
\\]Trong đó:
- \\(\overrightarrow{F}\\): Lực tác dụng lên điện tích thử \\(q\\).
- \\(q\\): Điện tích thử đặt trong điện trường.
Phương và chiều của \\(\overrightarrow{E}\\) trùng với phương và chiều của lực \\(\overrightarrow{F}\\) tác dụng lên điện tích dương.
- Vecto Cảm Ứng Từ (\\(\overrightarrow{B}\\)):
Đây là đại lượng vector đặc trưng cho từ trường tại một điểm, thể hiện lực từ tác dụng lên dây dẫn mang dòng điện. Độ lớn của vecto cảm ứng từ được tính bằng công thức:
\\[
\overrightarrow{F} = q(\overrightarrow{v} \times \overrightarrow{B})
\\]Trong đó:
- \\(q\\): Điện tích chuyển động trong từ trường.
- \\(\overrightarrow{v}\\): Vận tốc của điện tích.
- \\(\overrightarrow{B}\\): Vecto cảm ứng từ tại điểm mà điện tích chuyển động qua.
Phương của \\(\overrightarrow{B}\\) vuông góc với mặt phẳng chứa vecto vận tốc \\(\overrightarrow{v}\\) và lực từ \\(\overrightarrow{F}\\), xác định theo quy tắc bàn tay phải.
2. Công Thức Tính Toán
Các công thức tính toán cho vecto cường độ điện trường và vecto cảm ứng từ giúp xác định độ lớn và phương hướng của các đại lượng này trong các tình huống vật lý cụ thể. Dưới đây là các công thức chi tiết.
- Công Thức Tính Vecto Cường Độ Điện Trường (\\(\overrightarrow{E}\\)):
Cường độ điện trường tại một điểm được tính bằng công thức:
\\[
\overrightarrow{E} = \frac{\overrightarrow{F}}{q}
\\]Trong đó:
- \\(\overrightarrow{F}\\): Lực tác dụng lên điện tích thử \\(q\\).
- \\(q\\): Điện tích thử (đơn vị Coulomb).
Đối với một điện tích điểm, cường độ điện trường được tính bằng công thức:
\\[
E = k \cdot \frac{|Q|}{r^2}
\\]Trong đó:
- \\(k\\): Hằng số Coulomb (\\(k \approx 8.99 \times 10^9 \, \text{Nm}^2/\text{C}^2\\)).
- \\(Q\\): Điện tích gây ra điện trường.
- \\(r\\): Khoảng cách từ điện tích đến điểm đang xét.
- Công Thức Tính Vecto Cảm Ứng Từ (\\(\overrightarrow{B}\\)):
Vecto cảm ứng từ được tính thông qua lực từ tác dụng lên dây dẫn mang dòng điện theo công thức:
\\[
\overrightarrow{F} = I \cdot \overrightarrow{l} \times \overrightarrow{B}
\\]Trong đó:
- \\(I\\): Cường độ dòng điện trong dây dẫn (đơn vị Ampere).
- \\(\overrightarrow{l}\\): Độ dài đoạn dây dẫn trong từ trường (đơn vị mét).
- \\(\overrightarrow{B}\\): Vecto cảm ứng từ (đơn vị Tesla).
Độ lớn của vecto cảm ứng từ có thể được xác định bằng công thức:
\\[
B = \frac{F}{I \cdot l \cdot \sin \theta}
\\]Trong đó:
- \\(F\\): Lực từ tác dụng lên đoạn dây dẫn.
- \\(\theta\\): Góc giữa vecto cảm ứng từ và vecto chiều dòng điện.

3. Các Quy Tắc Liên Quan
Để xác định phương, chiều của các đại lượng vecto cường độ điện trường và vecto cảm ứng từ, cần tuân thủ một số quy tắc cơ bản. Dưới đây là các quy tắc phổ biến và cách áp dụng chúng.
- Quy Tắc Bàn Tay Phải:
Quy tắc này được sử dụng để xác định phương và chiều của vecto cường độ điện trường khi biết chiều dòng điện trong một dây dẫn thẳng.
- Đặt bàn tay phải sao cho ngón cái chỉ theo chiều dòng điện.
- Các ngón còn lại sẽ cuộn tròn theo chiều của đường sức điện trường xung quanh dây dẫn.
Phương của vecto cường độ điện trường là tiếp tuyến với các đường sức, và chiều của nó được xác định bởi chiều cuộn tròn của các ngón tay.
- Quy Tắc Bàn Tay Trái:
Quy tắc này dùng để xác định phương và chiều của lực từ tác dụng lên một dòng điện hoặc một điện tích chuyển động trong từ trường.
- Đặt bàn tay trái sao cho các đường sức từ xuyên vào lòng bàn tay.
- Ngón cái chỉ theo chiều dòng điện hoặc chiều chuyển động của điện tích.
- Ngón trỏ chỉ theo chiều vecto cảm ứng từ.
Chiều của lực từ tác dụng lên dòng điện hoặc điện tích sẽ được chỉ bởi ngón tay cái.
- Quy Tắc Nắm Tay Phải:
Quy tắc này áp dụng để xác định chiều của vecto cảm ứng từ xung quanh một dòng điện thẳng dài hoặc trong một cuộn dây.
- Đặt tay phải sao cho các ngón tay cuộn theo chiều dòng điện chạy qua cuộn dây.
- Ngón cái duỗi thẳng sẽ chỉ chiều của vecto cảm ứng từ trong lòng cuộn dây.
Phương của vecto cảm ứng từ là song song với trục của cuộn dây, và chiều của nó phụ thuộc vào chiều dòng điện theo quy tắc này.
XEM THÊM:
4. Ứng Dụng Thực Tiễn Trong Vật Lý
Vecto cường độ điện trường và vecto cảm ứng từ không chỉ là những khái niệm lý thuyết, mà còn có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau của vật lý và kỹ thuật. Dưới đây là một số ứng dụng thực tiễn đáng chú ý.
- Ứng Dụng Trong Truyền Thông:
Cả vecto cường độ điện trường và vecto cảm ứng từ đều đóng vai trò quan trọng trong công nghệ truyền thông. Anten phát sóng điện từ dựa trên sự dao động của các vecto này để truyền tải tín hiệu không dây trong các hệ thống viễn thông như sóng radio, TV, và mạng di động.
Ví dụ, sóng điện từ phát ra từ anten có cường độ phụ thuộc vào vecto cường độ điện trường tại điểm đó, cho phép truyền tải thông tin qua không gian mà không cần dây dẫn.
- Ứng Dụng Trong Thiết Kế Mạch Điện:
Vecto cảm ứng từ được sử dụng để thiết kế các mạch điện và các thiết bị như máy biến áp, động cơ điện, và máy phát điện. Trong những thiết bị này, từ trường được tạo ra bởi dòng điện qua cuộn dây, và lực từ tác động lên các phần tử trong mạch để thực hiện công việc cơ học.
Máy biến áp sử dụng nguyên lý này để thay đổi điện áp từ cao xuống thấp hoặc ngược lại, phục vụ cho việc truyền tải điện năng hiệu quả trên quãng đường dài.
- Ứng Dụng Trong Y Học:
Các vecto này còn có ứng dụng trong các thiết bị y tế, như máy MRI (Magnetic Resonance Imaging) sử dụng vecto cảm ứng từ để tạo ra hình ảnh chi tiết của các cơ quan nội tạng. Từ trường mạnh tạo ra bởi máy MRI tương tác với các proton trong cơ thể, từ đó thu thập dữ liệu để tái tạo hình ảnh.
- Ứng Dụng Trong Nghiên Cứu Khoa Học:
Vecto cường độ điện trường và vecto cảm ứng từ còn được sử dụng trong các nghiên cứu vật lý hiện đại, bao gồm cả việc nghiên cứu hạt cơ bản và tương tác giữa các lực cơ bản trong tự nhiên. Các thiết bị như máy gia tốc hạt sử dụng từ trường mạnh để dẫn hướng và tăng tốc các hạt ở vận tốc cao, từ đó khám phá các thuộc tính cơ bản của vật chất.

5. Mối Liên Hệ Giữa Điện Trường và Từ Trường
Điện trường và từ trường là hai hiện tượng vật lý có mối liên hệ mật thiết, đặc biệt trong bối cảnh của thuyết điện từ. Mối liên hệ này được thể hiện qua các hiện tượng và định luật cơ bản sau:
- Hiện Tượng Cảm Ứng Điện Từ:
Một trong những mối liên hệ rõ ràng nhất giữa điện trường và từ trường là hiện tượng cảm ứng điện từ. Khi một từ trường biến đổi theo thời gian, nó sinh ra một điện trường xoáy xung quanh, tạo ra dòng điện trong các dây dẫn, được gọi là dòng điện cảm ứng.
Hiện tượng này được diễn tả bởi định luật Faraday:
\\[
\mathcal{E} = -\frac{d\Phi_B}{dt}
\\]Trong đó:
- \\(\mathcal{E}\\): Suất điện động cảm ứng.
- \\(\Phi_B\\): Từ thông qua một mạch kín.
- Định Luật Ampère - Maxwell:
Định luật này mô tả mối liên hệ giữa dòng điện và từ trường. Nó cũng bao gồm yếu tố về điện trường biến đổi tạo ra từ trường, cho thấy rằng cả điện trường và từ trường có thể tương tác và tạo ra lẫn nhau.
Công thức tổng quát của định luật Ampère-Maxwell là:
\\[
\nabla \times \overrightarrow{B} = \mu_0 \overrightarrow{J} + \mu_0 \varepsilon_0 \frac{\partial \overrightarrow{E}}{\partial t}
\\]Trong đó:
- \\(\overrightarrow{B}\\): Vecto cảm ứng từ.
- \\(\overrightarrow{J}\\): Mật độ dòng điện.
- \\(\frac{\partial \overrightarrow{E}}{\partial t}\\): Sự biến thiên của điện trường theo thời gian.
- Sóng Điện Từ:
Sóng điện từ là kết quả của sự tương tác giữa điện trường và từ trường dao động. Khi một điện trường biến đổi, nó sinh ra một từ trường biến đổi vuông góc với nó, và ngược lại. Hai trường này lan truyền trong không gian dưới dạng sóng điện từ với tốc độ ánh sáng.
Các phương trình Maxwell mô tả chi tiết sự hình thành và lan truyền của sóng điện từ, đồng thời chỉ ra rằng điện trường và từ trường không thể tách rời trong quá trình này.