Chủ đề một chất điểm chuyển động theo phương trình: Chuyển động của một chất điểm theo phương trình là nền tảng quan trọng trong cơ học. Bài viết này sẽ giúp bạn hiểu rõ các phương trình cơ bản, ứng dụng trong thực tế và ví dụ minh họa. Hãy cùng khám phá cách các phương trình này mô tả chuyển động và ứng dụng của chúng trong các lĩnh vực khoa học và kỹ thuật.
Mục lục
Tổng Quan Về Chuyển Động Của Một Chất Điểm Theo Phương Trình
Chuyển động của một chất điểm theo phương trình là một chủ đề quan trọng trong cơ học và vật lý. Dưới đây là những điểm chính về chủ đề này:
1. Khái Niệm Cơ Bản
Chuyển động của một chất điểm được mô tả bằng các phương trình cơ học, mà thường là phương trình vi phân. Phương trình này có thể bao gồm chuyển động thẳng, chuyển động cong, hoặc chuyển động hỗn hợp.
2. Các Phương Trình Chính
- Phương trình chuyển động thẳng:
\[ x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 \] - Phương trình chuyển động cong:
\[ x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 + \frac{1}{6} b t^3 \]
3. Ứng Dụng Trong Thực Tế
Hiểu biết về chuyển động của chất điểm giúp giải quyết các bài toán trong nhiều lĩnh vực, như cơ học, kỹ thuật, và vật lý. Ví dụ, trong cơ học, các phương trình chuyển động được sử dụng để thiết kế hệ thống truyền động và phân tích lực tác động lên các vật thể.
4. Ví Dụ Minh Họa
| Ví Dụ | Phương Trình | Kết Quả |
|---|---|---|
| Chuyển động rơi tự do | \[ y(t) = \frac{1}{2} g t^2 \] | Khoảng cách rơi được tính dựa trên thời gian và gia tốc trọng trường. |
| Chuyển động đều | \[ v(t) = v_0 + a t \] | Tốc độ thay đổi theo thời gian với gia tốc không đổi. |
5. Các Tài Liệu Học Thuật
- Sách giáo khoa cơ học cơ bản
- Những bài giảng về phương trình chuyển động trong các khóa học đại học
- Bài báo nghiên cứu về ứng dụng của phương trình chuyển động trong kỹ thuật
6. Các Trang Web Hữu Ích
7. Nghiên Cứu Mới và Xu Hướng Tương Lai
Các nghiên cứu hiện tại đang tập trung vào việc tối ưu hóa các phương trình chuyển động cho các ứng dụng thực tiễn và phát triển các mô hình mới để dự đoán chính xác hơn chuyển động của chất điểm trong các điều kiện phức tạp.
.png)
1. Giới Thiệu Chung
Chuyển động của một chất điểm theo phương trình là một khái niệm quan trọng trong cơ học, mô tả cách một vật thể di chuyển theo các quy tắc vật lý. Để hiểu rõ hơn, chúng ta sẽ xem xét các yếu tố cơ bản và tầm quan trọng của việc nghiên cứu chuyển động này.
1.1. Khái Niệm Cơ Bản
Chất điểm là một mô hình lý thuyết trong vật lý, nơi chúng ta coi một vật thể có kích thước rất nhỏ để đơn giản hóa các tính toán về chuyển động của nó. Phương trình chuyển động mô tả cách vị trí của chất điểm thay đổi theo thời gian.
1.2. Tầm Quan Trọng Của Nghiên Cứu Chuyển Động
Nghiên cứu chuyển động giúp chúng ta hiểu rõ hơn về các lực tác động lên vật thể và các yếu tố ảnh hưởng đến chuyển động của nó. Điều này không chỉ quan trọng trong lý thuyết vật lý mà còn trong nhiều ứng dụng thực tiễn như thiết kế máy móc, phân tích kết cấu và mô phỏng hệ thống động lực học.
1.3. Các Loại Chuyển Động
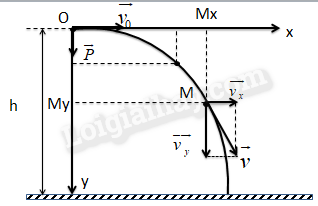
- Chuyển động thẳng: Di chuyển dọc theo một đường thẳng. Ví dụ, rơi tự do.
- Chuyển động cong: Di chuyển theo một đường cong, như chuyển động của quả bóng ném.
- Chuyển động hỗn hợp: Kết hợp nhiều loại chuyển động, ví dụ, chuyển động của một vệ tinh xung quanh Trái Đất.
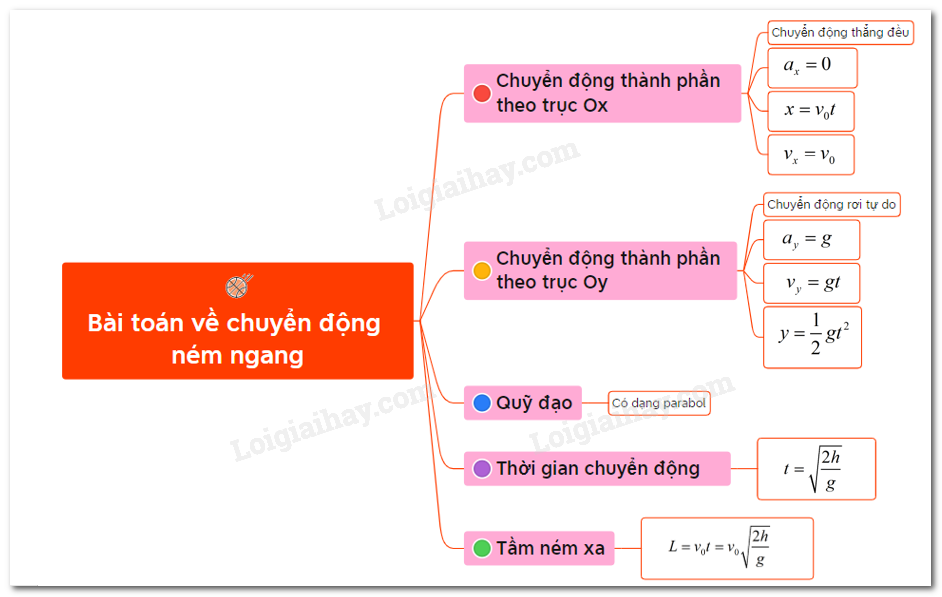
1.4. Các Phương Trình Chính
| Loại Phương Trình | Biểu Thức | Ý Nghĩa |
|---|---|---|
| Chuyển động thẳng đều | \[ x(t) = x_0 + v_0 t \] | Vị trí của chất điểm thay đổi theo thời gian với tốc độ không đổi. |
| Chuyển động thẳng biến đổi đều | \[ x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 \] | Vị trí của chất điểm thay đổi với gia tốc không đổi. |
| Chuyển động theo phương trình bậc ba | \[ x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 + \frac{1}{6} b t^3 \] | Vị trí của chất điểm với gia tốc thay đổi theo thời gian. |
2. Các Phương Trình Chuyển Động Chính
Chuyển động của một chất điểm có thể được mô tả bằng nhiều phương trình khác nhau tùy thuộc vào loại chuyển động. Dưới đây là các phương trình cơ bản thường được sử dụng trong phân tích chuyển động của chất điểm:
2.1. Chuyển Động Thẳng Đều
Chuyển động thẳng đều xảy ra khi một chất điểm di chuyển dọc theo một đường thẳng với tốc độ không đổi. Phương trình mô tả chuyển động này là:
\[ x(t) = x_0 + v_0 t \]
- \( x(t) \): Vị trí của chất điểm tại thời điểm \( t \).
- \( x_0 \): Vị trí ban đầu của chất điểm.
- \( v_0 \): Tốc độ của chất điểm (không đổi).
- \( t \): Thời gian trôi qua.
2.2. Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều xảy ra khi chất điểm di chuyển với gia tốc không đổi. Phương trình mô tả chuyển động này là:
\[ x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 \]
- \( x(t) \): Vị trí của chất điểm tại thời điểm \( t \).
- \( x_0 \): Vị trí ban đầu của chất điểm.
- \( v_0 \): Tốc độ ban đầu của chất điểm.
- \( a \): Gia tốc của chất điểm (không đổi).
- \( t \): Thời gian trôi qua.
2.3. Chuyển Động Theo Phương Trình Bậc Ba
Chuyển động theo phương trình bậc ba mô tả các trường hợp mà gia tốc thay đổi theo thời gian. Phương trình là:
\[ x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 + \frac{1}{6} b t^3 \]
- \( x(t) \): Vị trí của chất điểm tại thời điểm \( t \).
- \( x_0 \): Vị trí ban đầu của chất điểm.
- \( v_0 \): Tốc độ ban đầu của chất điểm.
- \( a \): Gia tốc ban đầu của chất điểm.
- \( b \): Thay đổi của gia tốc theo thời gian.
- \( t \): Thời gian trôi qua.
2.4. Phương Trình Chuyển Động Trong Hệ Quy Chiếu Đặc Biệt
Trong các hệ quy chiếu khác nhau, phương trình chuyển động có thể thay đổi. Một số ví dụ bao gồm:
- Chuyển động trong hệ quy chiếu quay: \[ x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 - \frac{1}{2} \omega^2 t^2 \]
- Chuyển động trong hệ quy chiếu phi địa phương: \[ x(t) = x_0 + v_0 t + \frac{1}{2} a t^2 + \frac{1}{2} \frac{g}{R} t^2 \]

5. Tài Liệu Học Thuật
Để tìm hiểu sâu về chuyển động của một chất điểm theo các phương trình khác nhau, có nhiều tài liệu học thuật có giá trị có thể tham khảo. Dưới đây là danh sách các tài liệu quan trọng mà bạn có thể sử dụng để nghiên cứu và học tập:
5.1. Sách Giáo Khoa và Sách Tham Khảo
- “Cơ học đại cương” - Tác giả: Đặng Văn Hùng
- “Vật lý học cơ bản” - Tác giả: Nguyễn Văn Lê
- “Đại cương về cơ học” - Tác giả: Trần Minh Hạnh
5.2. Tài Liệu Trực Tuyến
- Coursera - Cơ học cơ bản: Các khóa học miễn phí về cơ học cơ bản, bao gồm các chủ đề về chuyển động của chất điểm.
- Khan Academy - Phân tích chuyển động: Video và bài tập về chuyển động thẳng đều và chuyển động biến đổi đều.
- MIT OpenCourseWare - Cơ học cổ điển: Tài liệu học tập từ các khóa học cơ học của MIT.
5.3. Các Tạp Chí Khoa Học
- Journal of Mechanics: Các bài viết nghiên cứu về cơ học, bao gồm các phương trình chuyển động và ứng dụng của chúng.
- Physical Review E: Tạp chí nghiên cứu về cơ học và vật lý, cung cấp các bài viết nghiên cứu chi tiết về các phương trình chuyển động.
- Journal of Applied Physics: Cung cấp các nghiên cứu ứng dụng liên quan đến chuyển động của chất điểm.
5.4. Các Công Cụ Phân Tích và Mô Phỏng
- Matlab: Phần mềm mô phỏng và phân tích dữ liệu, hỗ trợ việc giải các phương trình chuyển động và mô phỏng chúng.
- Wolfram Mathematica: Công cụ tính toán và phân tích mạnh mẽ, hữu ích trong việc giải các phương trình chuyển động phức tạp.
- GeoGebra: Phần mềm hỗ trợ học tập toán học và cơ học, giúp trực quan hóa các phương trình chuyển động.

7. Nghiên Cứu Mới Và Xu Hướng Tương Lai
Trong lĩnh vực chuyển động của chất điểm, có nhiều nghiên cứu và xu hướng mới đang được phát triển. Dưới đây là những điểm nổi bật:
-
7.1. Công Nghệ Mới Trong Phân Tích Chuyển Động
Các công nghệ mới như cảm biến chuyển động và phân tích dữ liệu lớn đang mở ra khả năng phân tích chuyển động chính xác hơn. Các công nghệ này cho phép đo lường và mô phỏng chuyển động của chất điểm với độ chính xác cao.
- - Cung cấp cảm biến chuyển động và công nghệ phân tích dữ liệu.
- - Nền tảng phân tích dữ liệu lớn cho nghiên cứu chuyển động.
-
7.2. Các Mô Hình Dự Đo Chính Xác Hơn
Những nghiên cứu hiện tại đang tập trung vào việc phát triển các mô hình dự đoán chính xác hơn về chuyển động của chất điểm. Các mô hình này sử dụng các phương pháp toán học tiên tiến và dữ liệu thực nghiệm để cải thiện độ chính xác trong dự đoán chuyển động.
- - Các mô hình dự đoán và phân tích chuyển động tiên tiến.
- - Các nghiên cứu mới về mô hình hóa chuyển động chất điểm.