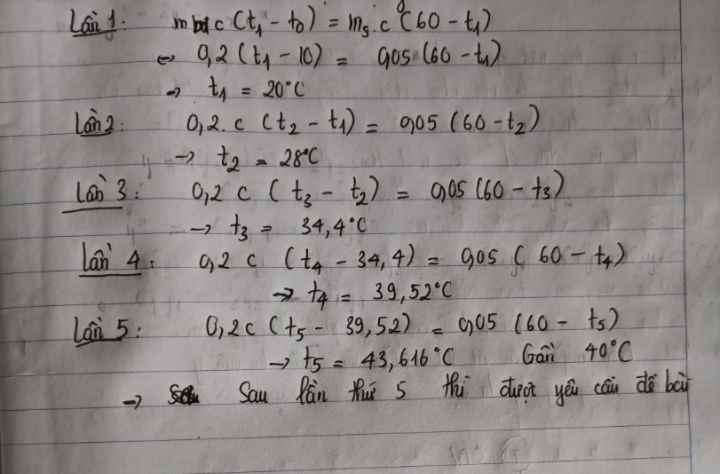Giải Bài Tập Công Thức Tính Nhiệt Lượng: Hướng Dẫn Chi Tiết Và Đáp Án Đầy Đủ

Công thức tính nhiệt lượng là một phần quan trọng trong chương trình học vật lý, đặc biệt là đối với học sinh lớp 8 và các lớp cao hơn. Dưới đây là tổng hợp các bài tập và hướng dẫn chi tiết cách giải các bài tập liên quan đến công thức này.

Công Thức Tính Nhiệt Lượng

Để tính nhiệt lượng \( Q \), ta sử dụng công thức:

\( Q = mc\Delta T \)

Trong đó:

• \( Q \) là nhiệt lượng (Joule - J)
• \( m \) là khối lượng của vật (kilogram - kg)
• \( c \) là nhiệt dung riêng của chất (J/kg.°C)
• \( \Delta T \) là độ tăng nhiệt độ (\( T_{2} - T_{1} \), tính bằng độ C)

Bài Tập Vận Dụng Công Thức Tính Nhiệt Lượng

1. Tính nhiệt lượng cần thiết để làm nóng 2kg nước từ 20°C lên 80°C.
2. Một thanh sắt có khối lượng 500g được nung nóng từ 25°C lên 75°C. Hỏi thanh sắt đã nhận được bao nhiêu nhiệt lượng? Biết nhiệt dung riêng của sắt là 460 J/kg.°C.
3. Một vật có khối lượng 1kg được cung cấp 5000J để tăng nhiệt độ từ 20°C lên 30°C. Tìm nhiệt dung riêng của vật liệu làm nên vật.
4. Tính nhiệt lượng tỏa ra khi làm nguội 1kg đồng từ 100°C xuống 25°C. Biết nhiệt dung riêng của đồng là 385 J/kg.°C.

Hướng Dẫn Giải Chi Tiết

Bài 1:

Áp dụng công thức tính nhiệt lượng \( Q = mc\Delta T \)

Với:

• Khối lượng nước \( m = 2 \, \text{kg} \)
• Nhiệt dung riêng của nước \( c = 4200 \, \text{J/kg.°C} \)
• Độ tăng nhiệt độ \( \Delta T = 80°C - 20°C = 60°C \)

Tính toán:

\( Q = 2 \times 4200 \times 60 = 504,000 \, \text{J} = 504 \, \text{kJ} \)

Bài 2:

Áp dụng công thức \( Q = mc\Delta T \), ta có:

• Khối lượng thanh sắt \( m = 0.5 \, \text{kg} \)
• Nhiệt dung riêng của sắt \( c = 460 \, \text{J/kg.°C} \)
• Độ tăng nhiệt độ \( \Delta T = 75°C - 25°C = 50°C \)

Tính toán:

\( Q = 0.5 \times 460 \times 50 = 11,500 \, \text{J} \)

Bài 3:

Áp dụng công thức \( Q = mc\Delta T \) để tìm nhiệt dung riêng \( c \):

• Khối lượng vật \( m = 1 \, \text{kg} \)
• Độ tăng nhiệt độ \( \Delta T = 30°C - 20°C = 10°C \)
• Nhiệt lượng \( Q = 5000 \, \text{J} \)

Tính toán:

\( c = \frac{Q}{m\Delta T} = \frac{5000}{1 \times 10} = 500 \, \text{J/kg.°C} \)

Bài 4:

Áp dụng công thức \( Q = mc\Delta T \) với:

• Khối lượng đồng \( m = 1 \, \text{kg} \)
• Nhiệt dung riêng của đồng \( c = 385 \, \text{J/kg.°C} \)
• Độ giảm nhiệt độ \( \Delta T = 100°C - 25°C = 75°C \)

Tính toán:

\( Q = 1 \times 385 \times 75 = 28,875 \, \text{J} \)

Kết Luận

Các bài tập về công thức tính nhiệt lượng giúp học sinh hiểu rõ hơn về cách thức truyền nhiệt, nhiệt dung riêng và mối quan hệ giữa nhiệt lượng với khối lượng, nhiệt độ và nhiệt dung riêng. Việc nắm vững công thức và phương pháp giải giúp các em dễ dàng áp dụng vào các bài toán thực tế.

Nhiệt lượng là một dạng năng lượng chuyển đổi giữa các vật thể hoặc các hệ vật thể khi có sự chênh lệch về nhiệt độ. Khi một vật thể nhận nhiệt, năng lượng sẽ truyền từ môi trường xung quanh vào vật, khiến nhiệt độ của nó tăng lên. Ngược lại, khi vật thể mất nhiệt, năng lượng sẽ truyền từ vật vào môi trường xung quanh, làm nhiệt độ của nó giảm xuống.

Công thức tính nhiệt lượng được sử dụng để xác định lượng nhiệt mà một vật thể cần thu vào hoặc toả ra trong quá trình thay đổi nhiệt độ. Công thức cơ bản của nhiệt lượng được biểu diễn như sau:

\( Q = m \cdot c \cdot \Delta t \)

Trong đó:

• Q: Nhiệt lượng (đơn vị: Joule - J)
• m: Khối lượng của vật (đơn vị: Kilogram - kg)
• c: Nhiệt dung riêng của chất làm nên vật (đơn vị: J/kg.K)
• \(\Delta t\): Độ thay đổi nhiệt độ của vật (đơn vị: °C hoặc K)

Để hiểu rõ hơn về công thức này, hãy xem xét các yếu tố ảnh hưởng đến nhiệt lượng:

1. Khối lượng của vật: Khối lượng càng lớn, nhiệt lượng cần để thay đổi nhiệt độ của vật càng cao.
2. Nhiệt dung riêng: Mỗi chất có một nhiệt dung riêng khác nhau, biểu thị khả năng hấp thụ nhiệt của chất đó.
3. Độ thay đổi nhiệt độ: Sự thay đổi nhiệt độ càng lớn thì nhiệt lượng trao đổi càng nhiều.

Như vậy, để tính toán nhiệt lượng chính xác, cần xác định rõ các yếu tố trên và áp dụng công thức một cách chính xác trong từng bài toán cụ thể.

Nhiệt lượng mà một vật thể thu vào hoặc toả ra không chỉ phụ thuộc vào bản chất của vật liệu mà còn chịu ảnh hưởng bởi nhiều yếu tố khác. Dưới đây là các yếu tố chính ảnh hưởng đến nhiệt lượng:

1. Khối lượng của vật: Khối lượng càng lớn thì nhiệt lượng cần thiết để thay đổi nhiệt độ của vật càng nhiều. Điều này được lý giải bởi việc cần nhiều năng lượng hơn để làm nóng hoặc làm lạnh một vật thể có khối lượng lớn.
2. Nhiệt dung riêng của vật liệu: Nhiệt dung riêng (\(c\)) là lượng nhiệt cần thiết để làm tăng 1 kg chất lên 1°C. Mỗi vật liệu có một nhiệt dung riêng khác nhau. Chẳng hạn, nước có nhiệt dung riêng cao, có nghĩa là cần nhiều nhiệt lượng để thay đổi nhiệt độ của nó so với kim loại.
3. Độ thay đổi nhiệt độ (\(\Delta t\)): Sự thay đổi nhiệt độ của vật càng lớn thì nhiệt lượng trao đổi càng nhiều. Ví dụ, để làm nóng nước từ 20°C lên 30°C cần ít nhiệt lượng hơn so với việc làm nóng từ 20°C lên 50°C.
4. Điều kiện môi trường: Các điều kiện như áp suất, độ ẩm và dòng nhiệt từ môi trường xung quanh cũng ảnh hưởng đến tốc độ và mức độ nhiệt lượng mà vật thể có thể trao đổi.
5. Cách thức truyền nhiệt: Nhiệt có thể truyền qua các vật thể bằng ba cách chính: dẫn nhiệt, đối lưu và bức xạ. Mỗi phương pháp truyền nhiệt ảnh hưởng khác nhau đến tốc độ và lượng nhiệt được trao đổi.

Hiểu rõ các yếu tố này sẽ giúp bạn áp dụng chính xác công thức tính nhiệt lượng trong các tình huống cụ thể, đảm bảo kết quả tính toán đúng đắn và hiệu quả.

Trong thực tế, việc tính toán nhiệt lượng có thể được áp dụng trong nhiều tình huống khác nhau. Dưới đây là các phương pháp tính nhiệt lượng cho từng trường hợp cụ thể:

1. Tính nhiệt lượng khi làm nóng hoặc làm lạnh một chất:

   Phương pháp này thường được áp dụng khi bạn cần tính toán nhiệt lượng để thay đổi nhiệt độ của một chất từ nhiệt độ ban đầu \(T_1\) đến nhiệt độ cuối \(T_2\). Công thức sử dụng:

   \( Q = m \cdot c \cdot (T_2 - T_1) \)

   Trong đó:

   • \(Q\) là nhiệt lượng cần tính (J)
   • \(m\) là khối lượng của chất (kg)
   • \(c\) là nhiệt dung riêng của chất (J/kg.K)
   • \(T_2 - T_1\) là độ thay đổi nhiệt độ (°C hoặc K)
2. Tính nhiệt lượng trong quá trình truyền nhiệt qua vật liệu:

   Khi nhiệt truyền qua một lớp vật liệu, bạn có thể sử dụng công thức sau để tính nhiệt lượng:

   \( Q = \frac{k \cdot A \cdot \Delta T \cdot t}{d} \)

   Trong đó:

   • \(k\) là hệ số dẫn nhiệt của vật liệu (W/m.K)
   • \(A\) là diện tích bề mặt truyền nhiệt (m²)
   • \(\Delta T\) là độ chênh lệch nhiệt độ giữa hai mặt của vật liệu (°C hoặc K)
   • \(t\) là thời gian truyền nhiệt (s)
   • \(d\) là độ dày của lớp vật liệu (m)
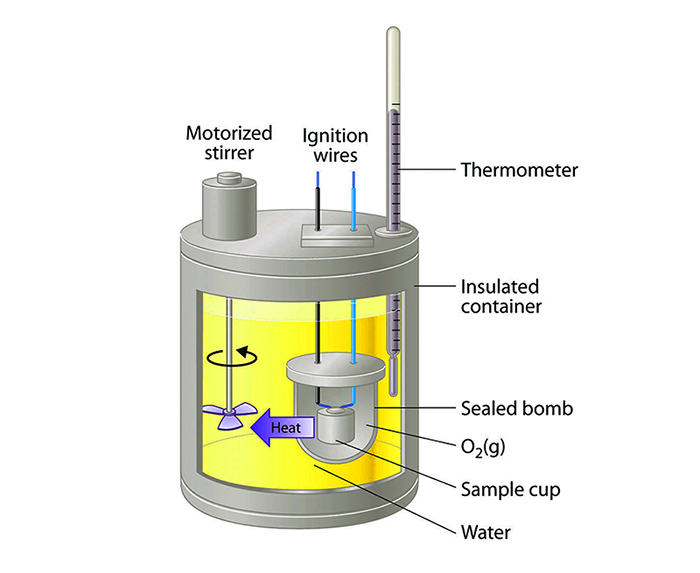
3. Tính nhiệt lượng trong phản ứng hóa học:

   Đối với các phản ứng hóa học tỏa nhiệt hoặc thu nhiệt, nhiệt lượng có thể được tính toán thông qua công thức:

   \( Q = \Delta H \cdot n \)

   Trong đó:

   • \(\Delta H\) là biến thiên enthalpy của phản ứng (kJ/mol)
   • \(n\) là số mol của chất tham gia phản ứng (mol)
4. Tính nhiệt lượng trong quá trình đối lưu:

   Trong các quá trình đối lưu, nhiệt lượng được tính dựa trên hệ số đối lưu và diện tích bề mặt tiếp xúc:

   \( Q = h \cdot A \cdot \Delta T \cdot t \)

   Trong đó:

   • \(h\) là hệ số đối lưu (W/m².K)
   • \(A\) là diện tích bề mặt tiếp xúc (m²)
   • \(\Delta T\) là chênh lệch nhiệt độ giữa bề mặt và chất lưu (°C hoặc K)
   • \(t\) là thời gian diễn ra quá trình (s)

Việc áp dụng đúng phương pháp tính toán trong từng tình huống cụ thể giúp đảm bảo độ chính xác và hiệu quả trong việc giải quyết các bài toán liên quan đến nhiệt lượng.

Để hiểu rõ và nắm vững cách áp dụng công thức tính nhiệt lượng, hãy cùng thực hành với một số bài tập cụ thể dưới đây. Các bài tập này được thiết kế để giúp bạn củng cố kiến thức và phát triển kỹ năng giải toán liên quan đến nhiệt lượng.

1. Bài tập 1: Tính nhiệt lượng cần để làm nóng nước

   Giả sử bạn có 2 kg nước ở nhiệt độ 20°C. Hãy tính nhiệt lượng cần thiết để làm nóng nước đến 80°C. Biết rằng nhiệt dung riêng của nước là 4200 J/kg.K.

   Giải:

   Áp dụng công thức tính nhiệt lượng:

   \( Q = m \cdot c \cdot \Delta t \)

   Với:

   • m = 2 kg
   • c = 4200 J/kg.K
   • \(\Delta t = 80°C - 20°C = 60°C\)

   Thay các giá trị vào công thức:

   \( Q = 2 \cdot 4200 \cdot 60 = 504,000 \, J \)

   Vậy nhiệt lượng cần để làm nóng 2 kg nước từ 20°C lên 80°C là 504,000 J.

2. Bài tập 2: Tính nhiệt lượng mất đi khi làm lạnh kim loại

   Một khối kim loại có khối lượng 500 g được làm lạnh từ 150°C xuống 25°C. Biết nhiệt dung riêng của kim loại là 900 J/kg.K. Hãy tính nhiệt lượng mà khối kim loại này mất đi.

   Giải:

   Đầu tiên, đổi khối lượng từ gam sang kilogam:

   \( m = 500 \, g = 0.5 \, kg \)

   Sau đó, áp dụng công thức tính nhiệt lượng:

   \( Q = m \cdot c \cdot \Delta t \)

   Với:

   • m = 0.5 kg
   • c = 900 J/kg.K
   • \(\Delta t = 25°C - 150°C = -125°C\)

   Thay các giá trị vào công thức:

   \( Q = 0.5 \cdot 900 \cdot (-125) = -56,250 \, J \)

   Nhiệt lượng mất đi là 56,250 J. Dấu âm cho thấy đây là quá trình toả nhiệt.

3. Bài tập 3: Tính nhiệt lượng trong phản ứng hóa học

   Trong một phản ứng hóa học, 0.1 mol chất A tỏa ra một nhiệt lượng 150 kJ. Hãy tính nhiệt lượng tổng cộng được giải phóng nếu có 0.5 mol chất A tham gia phản ứng.

   Giải:

   Sử dụng công thức tính nhiệt lượng trong phản ứng hóa học:

   \( Q = \Delta H \cdot n \)

   Với:

   • \(\Delta H = 150 \, kJ \)
   • \( n = 0.5 \, mol \)

   Thay các giá trị vào công thức:

   \( Q = 150 \cdot 0.5 = 75 \, kJ \)

   Nhiệt lượng tổng cộng được giải phóng là 75 kJ.

Các bài tập trên giúp bạn làm quen với cách sử dụng công thức tính nhiệt lượng trong các tình huống khác nhau. Việc thực hành đều đặn sẽ giúp bạn nắm vững kiến thức và giải bài tập nhanh chóng, chính xác.

Dưới đây là lời giải chi tiết cho một số bài tập tiêu biểu về công thức tính nhiệt lượng. Các bài tập này sẽ giúp bạn hiểu rõ hơn về cách áp dụng các công thức trong các tình huống cụ thể.

1. Bài tập 1: Tính nhiệt lượng để đun nóng nước

   Đề bài: Hãy tính nhiệt lượng cần thiết để đun nóng 3 kg nước từ 25°C lên 100°C. Biết nhiệt dung riêng của nước là 4200 J/kg.K.

   Lời giải:

   Bước 1: Xác định các thông số đã cho:

   • Khối lượng nước: \( m = 3 \, kg \)
   • Nhiệt dung riêng của nước: \( c = 4200 \, J/kg.K \)
   • Độ tăng nhiệt độ: \( \Delta t = 100°C - 25°C = 75°C \)

   Bước 2: Áp dụng công thức tính nhiệt lượng:

   \( Q = m \cdot c \cdot \Delta t \)

   Bước 3: Thay các giá trị vào công thức:

   \( Q = 3 \cdot 4200 \cdot 75 = 945,000 \, J \)

   Vậy, nhiệt lượng cần thiết để đun nóng 3 kg nước từ 25°C lên 100°C là 945,000 J.

2. Bài tập 2: Tính nhiệt lượng tỏa ra khi làm lạnh một khối kim loại

   Đề bài: Một khối kim loại có khối lượng 2 kg được làm lạnh từ 200°C xuống 50°C. Nhiệt dung riêng của kim loại là 500 J/kg.K. Hãy tính nhiệt lượng tỏa ra.

   Lời giải:

   Bước 1: Xác định các thông số đã cho:

   • Khối lượng kim loại: \( m = 2 \, kg \)
   • Nhiệt dung riêng của kim loại: \( c = 500 \, J/kg.K \)
   • Độ giảm nhiệt độ: \( \Delta t = 50°C - 200°C = -150°C \)

   Bước 2: Áp dụng công thức tính nhiệt lượng:

   \( Q = m \cdot c \cdot \Delta t \)

   Bước 3: Thay các giá trị vào công thức:

   \( Q = 2 \cdot 500 \cdot (-150) = -150,000 \, J \)

   Vậy, nhiệt lượng tỏa ra khi làm lạnh khối kim loại là 150,000 J (dấu âm thể hiện sự tỏa nhiệt).

3. Bài tập 3: Tính nhiệt lượng trong phản ứng hóa học

   Đề bài: Trong một phản ứng hóa học, 0.2 mol một chất tỏa ra 200 kJ nhiệt lượng. Hãy tính nhiệt lượng tỏa ra khi có 1 mol chất này phản ứng.

   Lời giải:

   Bước 1: Xác định các thông số đã cho:

   • Số mol chất ban đầu: \( n_1 = 0.2 \, mol \)
   • Nhiệt lượng tỏa ra: \( Q_1 = 200 \, kJ \)
   • Số mol chất cần tính: \( n_2 = 1 \, mol \)

   Bước 2: Sử dụng quy tắc tỉ lệ để tính nhiệt lượng tỏa ra:

   \( Q_2 = Q_1 \cdot \frac{n_2}{n_1} \)

   Bước 3: Thay các giá trị vào công thức:

   \( Q_2 = 200 \cdot \frac{1}{0.2} = 1000 \, kJ \)

   Vậy, nhiệt lượng tỏa ra khi 1 mol chất phản ứng là 1000 kJ.

Các lời giải trên cung cấp các bước chi tiết giúp bạn dễ dàng hiểu và áp dụng các công thức tính nhiệt lượng vào bài tập thực tế. Việc luyện tập đều đặn sẽ giúp bạn nắm vững kiến thức và giải quyết các bài toán về nhiệt lượng một cách tự tin.