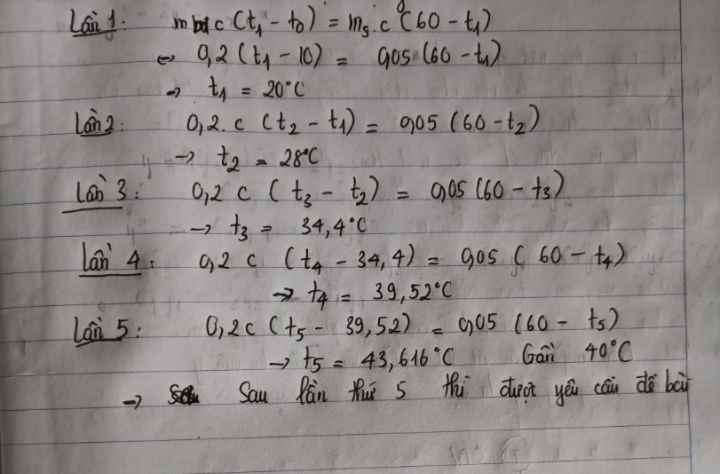Bài Tập Công Thức Tính Nhiệt Lượng - Hướng Dẫn Chi Tiết và Ví Dụ Thực Tế

Công thức tính nhiệt lượng là một phần quan trọng trong chương trình học Vật lý. Nhiệt lượng được định nghĩa là năng lượng được truyền từ vật này sang vật khác khi có sự thay đổi nhiệt độ. Dưới đây là các công thức và bài tập liên quan đến nhiệt lượng, giúp học sinh hiểu rõ hơn về cách áp dụng các công thức vào thực tế.

1. Công Thức Tính Nhiệt Lượng

Nhiệt lượng \(Q\) được tính theo công thức:

\[
Q = m \cdot c \cdot \Delta t
\]
Trong đó:

• \(Q\): Nhiệt lượng (Joule)
• \(m\): Khối lượng của vật (kg)
• \(c\): Nhiệt dung riêng của chất làm nên vật (J/kg.K)
• \(\Delta t\): Độ thay đổi nhiệt độ (°C hoặc K)

2. Ví Dụ Bài Tập

Bài Tập 1:

Tính nhiệt lượng cần cung cấp để làm nóng 2 kg nước từ 20°C đến 100°C. Biết nhiệt dung riêng của nước là \(c = 4200 \, \text{J/kg.K}\).

Lời giải:

Áp dụng công thức tính nhiệt lượng:
\[
Q = m \cdot c \cdot \Delta t = 2 \, \text{kg} \cdot 4200 \, \text{J/kg.K} \cdot (100°C - 20°C) = 672000 \, \text{J}
\]
Vậy, nhiệt lượng cần cung cấp là \(672000 \, \text{J}\).

Bài Tập 2:

Một khối sắt có khối lượng 5 kg được nung nóng từ 30°C đến 80°C. Tính nhiệt lượng mà khối sắt này nhận được. Biết nhiệt dung riêng của sắt là \(c = 460 \, \text{J/kg.K}\).

Lời giải:

Áp dụng công thức tính nhiệt lượng:
\[
Q = m \cdot c \cdot \Delta t = 5 \, \text{kg} \cdot 460 \, \text{J/kg.K} \cdot (80°C - 30°C) = 115000 \, \text{J}
\]
Vậy, nhiệt lượng mà khối sắt nhận được là \(115000 \, \text{J}\).

3. Lưu Ý Khi Áp Dụng Công Thức

• Đảm bảo các đơn vị đo lường phải thống nhất khi áp dụng công thức, chẳng hạn khối lượng phải tính bằng kg, nhiệt độ bằng °C hoặc K.
• Nhiệt dung riêng \(c\) của các chất có thể thay đổi tùy vào điều kiện nhiệt độ, do đó cần sử dụng giá trị \(c\) phù hợp với điều kiện bài toán.
• Chỉ sử dụng công thức này cho các quá trình biến đổi nhiệt độ không quá lớn và trong phạm vi nhất định, nơi nhiệt dung riêng có thể coi là hằng số.

4. Bài Tập Tự Luyện

1. Tính nhiệt lượng cần thiết để làm nóng 3 kg đồng từ 25°C đến 75°C. Biết nhiệt dung riêng của đồng là 390 J/kg.K.
2. Một tấm nhôm có khối lượng 1,5 kg được nung từ 20°C đến 70°C. Tính nhiệt lượng mà tấm nhôm nhận được. Biết nhiệt dung riêng của nhôm là 900 J/kg.K.
3. Tính nhiệt lượng mất đi khi 2 kg nước ở 100°C bị làm nguội đến 50°C. Biết nhiệt dung riêng của nước là 4200 J/kg.K.

Những bài tập trên giúp củng cố kiến thức và kỹ năng áp dụng công thức tính nhiệt lượng trong các tình huống thực tế. Các học sinh nên luyện tập thường xuyên để nắm vững các khái niệm và công thức.

Công thức nhiệt lượng cơ bản được sử dụng để tính nhiệt lượng \( Q \) mà một vật hấp thụ hoặc tỏa ra khi nhiệt độ thay đổi. Công thức này được biểu diễn bằng phương trình:

\( Q = mc\Delta t \)

Trong đó:

• \( Q \) là nhiệt lượng (đơn vị: Joule, J)
• \( m \) là khối lượng của vật (đơn vị: kg)
• \( c \) là nhiệt dung riêng của chất làm nên vật (đơn vị: J/kg.K)
• \( \Delta t \) là độ biến thiên nhiệt độ (đơn vị: °C hoặc K)

Bước 1: Xác định các đại lượng cần thiết

Trước hết, bạn cần xác định các đại lượng \( m \), \( c \) và \( \Delta t \) từ đề bài hoặc từ thông tin thực nghiệm.

Bước 2: Thay các giá trị vào công thức

Tiếp theo, thay các giá trị của \( m \), \( c \) và \( \Delta t \) vào công thức \( Q = mc\Delta t \) để tính toán nhiệt lượng \( Q \).

Bước 3: Tính toán và đưa ra kết quả

Sau khi thực hiện các phép tính cần thiết, bạn sẽ có được giá trị của \( Q \), đây là lượng nhiệt mà vật đã hấp thụ hoặc tỏa ra.

Ví dụ:

• Giả sử bạn có một cốc nước với khối lượng \( m = 0.5 \, \text{kg} \), nhiệt dung riêng của nước là \( c = 4180 \, \text{J/kg.K} \), và nhiệt độ của nước tăng từ \( 20^\circ C \) lên \( 30^\circ C \) (tức \( \Delta t = 10^\circ C \)).
• Thay các giá trị vào công thức: \( Q = 0.5 \times 4180 \times 10 = 20900 \, \text{J} \).
• Kết quả: Nhiệt lượng mà nước hấp thụ là \( 20900 \, \text{J} \).

Nhận xét: Phương pháp này áp dụng đơn giản cho các bài tập liên quan đến sự thay đổi nhiệt độ của một vật, đặc biệt trong các bài toán cơ bản.

Trong các bài toán hỗn hợp, chúng ta thường phải tính toán nhiệt lượng trong các hệ thống gồm nhiều vật hoặc chất khác nhau khi chúng được trộn lẫn. Phương pháp này yêu cầu áp dụng nguyên lý bảo toàn nhiệt lượng, theo đó tổng nhiệt lượng hấp thụ bằng tổng nhiệt lượng tỏa ra.

Bước 1: Xác định các đại lượng liên quan

Xác định các đại lượng như khối lượng \( m \), nhiệt dung riêng \( c \), và sự thay đổi nhiệt độ \( \Delta t \) của từng vật hoặc chất trong hỗn hợp.

Bước 2: Viết phương trình bảo toàn nhiệt lượng

Viết phương trình bảo toàn nhiệt lượng, với nhiệt lượng tổng của hệ bằng 0:

\( Q_1 + Q_2 + Q_3 + ... + Q_n = 0 \)

Trong đó:

• \( Q_1, Q_2, ... Q_n \) là nhiệt lượng của các vật hoặc chất khác nhau trong hệ, được tính bằng công thức \( Q = mc\Delta t \).
• Nếu một vật tỏa nhiệt, \( Q \) sẽ mang dấu âm; nếu hấp thụ nhiệt, \( Q \) sẽ mang dấu dương.

Bước 3: Thay giá trị và giải phương trình

Thay các giá trị đã xác định vào phương trình bảo toàn nhiệt lượng và giải phương trình để tìm ra nhiệt độ cuối cùng hoặc nhiệt lượng của từng thành phần trong hệ.

Ví dụ:

• Giả sử bạn có hai cốc nước, cốc 1 có khối lượng \( m_1 = 0.5 \, \text{kg} \), nhiệt dung riêng \( c_1 = 4180 \, \text{J/kg.K} \), nhiệt độ ban đầu \( t_1 = 80^\circ C \); cốc 2 có khối lượng \( m_2 = 0.3 \, \text{kg} \), nhiệt dung riêng \( c_2 = 4180 \, \text{J/kg.K} \), nhiệt độ ban đầu \( t_2 = 20^\circ C \).
• Áp dụng phương trình bảo toàn nhiệt lượng: \( Q_1 + Q_2 = 0 \), ta có:

\( m_1c_1(t_f - t_1) + m_2c_2(t_f - t_2) = 0 \)

• Giải phương trình để tìm nhiệt độ cuối cùng \( t_f \).

Nhận xét: Áp dụng nhiệt lượng trong các bài toán hỗn hợp giúp giải quyết nhiều bài toán thực tế liên quan đến sự trao đổi nhiệt giữa các chất khác nhau trong hệ kín.

Trong các quá trình chuyển thể (từ rắn sang lỏng, từ lỏng sang khí, v.v.), ta cần tính nhiệt lượng cần cung cấp hoặc toả ra khi chất thay đổi trạng thái. Để tính nhiệt lượng trong quá trình chuyển thể, ta sử dụng công thức:

\[
Q = m \cdot \lambda
\]

Trong đó:

• Q: Nhiệt lượng (Joules, J)
• m: Khối lượng của chất (kilograms, kg)
• \(\lambda\): Nhiệt ẩn của quá trình chuyển thể (Joules/kg)

Ví dụ bài tập về quá trình chuyển thể

Ví dụ 1: Tính nhiệt lượng cần thiết để làm nóng chảy 500g nước đá ở 0°C thành nước lỏng. Biết rằng nhiệt ẩn nóng chảy của nước đá là 334 kJ/kg.

Lời giải chi tiết

Bước 1: Xác định khối lượng nước đá cần làm nóng chảy.

\( m = 500g = 0.5 kg \)

Bước 2: Sử dụng công thức tính nhiệt lượng:

\[
Q = m \cdot \lambda
\]

Với \( \lambda = 334 kJ/kg = 334 \times 10^3 J/kg \)

Bước 3: Thay số vào công thức:

\[
Q = 0.5 \times 334 \times 10^3 = 167,000 J = 167 kJ
\]

Vậy nhiệt lượng cần cung cấp để làm nóng chảy 500g nước đá là 167 kJ.

Nhận xét và lưu ý

• Khi tính toán nhiệt lượng trong các quá trình chuyển thể, cần chú ý đơn vị của các đại lượng.
• Chỉ sử dụng công thức này khi chất thay đổi trạng thái mà không thay đổi nhiệt độ.
• Nhiệt lượng có thể toả ra hoặc hấp thụ tuỳ vào quá trình chuyển thể là toả nhiệt hay thu nhiệt.

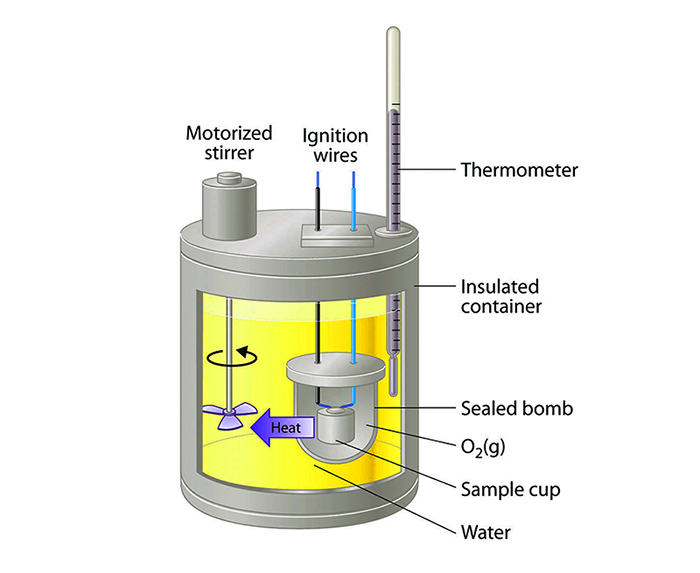
Trong các hệ thống phức tạp, việc tính toán nhiệt lượng không chỉ dừng lại ở các bài toán đơn giản về truyền nhiệt giữa hai vật thể mà còn liên quan đến các hệ thống có nhiều thành phần tương tác với nhau. Các bài toán này đòi hỏi sự áp dụng của các công thức nhiệt lượng mở rộng và tính cân bằng nhiệt giữa các thành phần của hệ thống. Sau đây là một ví dụ chi tiết về bài tập liên quan đến hệ thống phức tạp:

Bài toán: Tính nhiệt lượng trong hệ thống nước và sắt

Cho một hệ thống gồm một bình chứa 5 kg nước ở nhiệt độ 60°C và một thanh sắt có khối lượng 2 kg đã được nung nóng đến nhiệt độ 500°C. Hãy tính nhiệt độ cân bằng của hệ thống khi cả nước và sắt đã đạt cân bằng nhiệt. Biết rằng nhiệt dung riêng của nước là 4184 J/kg.K và của sắt là 460 J/kg.K.

Giải:

1. Bước 1: Xác định thông số đầu vào
   • Khối lượng nước: \( m_1 = 5 \, \text{kg} \)
   • Khối lượng sắt: \( m_2 = 2 \, \text{kg} \)
   • Nhiệt dung riêng của nước: \( c_1 = 4184 \, \text{J/kg.K} \)
   • Nhiệt dung riêng của sắt: \( c_2 = 460 \, \text{J/kg.K} \)
   • Nhiệt độ ban đầu của nước: \( t_1 = 60^{\circ}C \)
   • Nhiệt độ ban đầu của sắt: \( t_2 = 500^{\circ}C \)
2. Bước 2: Sử dụng phương trình cân bằng nhiệt

   Theo định luật bảo toàn năng lượng, tổng nhiệt lượng thu vào bằng tổng nhiệt lượng tỏa ra. Nhiệt lượng mà nước nhận được sẽ bằng nhiệt lượng mà sắt tỏa ra:

   \[
   Q_1 = Q_2
   \]

   Từ đó ta có phương trình:

   \[
   m_1 \cdot c_1 \cdot (t - t_1) = m_2 \cdot c_2 \cdot (t_2 - t)
   \]

   Trong đó:

   • \( t \) là nhiệt độ cân bằng cần tìm
   • \( t_1 \) và \( t_2 \) lần lượt là nhiệt độ ban đầu của nước và sắt
3. Bước 3: Thay giá trị vào phương trình

   Thay các giá trị đã biết vào phương trình cân bằng nhiệt:

   \[
   5 \cdot 4184 \cdot (t - 60) = 2 \cdot 460 \cdot (500 - t)
   \]

   Giải phương trình trên để tìm nhiệt độ cân bằng \( t \).

4. Bước 4: Tính toán và kết quả

   Giải phương trình ta được:

   \[
   t = 100.8^{\circ}C
   \]

   Vậy nhiệt độ cân bằng của hệ thống là \( t = 100.8^{\circ}C \).

Kết luận:

Các bài toán về nhiệt lượng trong hệ thống phức tạp đòi hỏi khả năng áp dụng các công thức nhiệt lượng một cách linh hoạt và đúng đắn. Việc tính toán này rất quan trọng trong các ứng dụng thực tiễn như kỹ thuật nhiệt, hóa học và công nghiệp.

Trong đời sống hàng ngày, việc tính toán và ứng dụng nhiệt lượng giúp chúng ta hiểu rõ hơn về cách thức mà nhiệt lượng được truyền tải và tiêu thụ. Dưới đây là một số bài tập ứng dụng nhiệt lượng trong thực tế giúp bạn nắm rõ hơn về khái niệm này.

• Bài tập 1: Tính nhiệt lượng cần thiết để đun sôi nước.

Giả sử chúng ta cần đun sôi 2 lít nước từ nhiệt độ ban đầu là 25°C lên 100°C. Nhiệt dung riêng của nước là 4200 J/kg.K.

1. Khối lượng của nước:
   m = 2 kg (vì 1 lít nước có khối lượng tương đương 1 kg)
2. Độ tăng nhiệt độ:
   Δt = 100°C - 25°C = 75°C
3. Công thức tính nhiệt lượng:
   Q = m . c . Δt = 2 . 4200 . 75 = 630,000 J
4. Kết quả:
   Nhiệt lượng cần thiết để đun sôi 2 lít nước từ 25°C lên 100°C là 630 kJ.
• Bài tập 2: Tính nhiệt lượng hấp thụ từ ánh sáng Mặt Trời.

Giả sử một hồ nước ngoài trời có khối lượng nước là 500 kg. Trong một ngày nắng, nhiệt độ nước tăng từ 22°C lên 30°C. Nhiệt dung riêng của nước vẫn là 4200 J/kg.K.

1. Khối lượng nước:
   m = 500 kg
2. Độ tăng nhiệt độ:
   Δt = 30°C - 22°C = 8°C
3. Công thức tính nhiệt lượng:
   Q = m . c . Δt = 500 . 4200 . 8 = 16,800,000 J
4. Kết quả:
   Nước đã hấp thụ 16.8 MJ nhiệt lượng từ ánh sáng Mặt Trời trong ngày.
• Bài tập 3: Tính nhiệt lượng tiêu thụ khi làm nóng kim loại.

Giả sử chúng ta muốn làm nóng một miếng đồng có khối lượng 3 kg từ nhiệt độ 15°C lên 75°C. Nhiệt dung riêng của đồng là 380 J/kg.K.

1. Khối lượng của đồng:
   m = 3 kg
2. Độ tăng nhiệt độ:
   Δt = 75°C - 15°C = 60°C
3. Công thức tính nhiệt lượng:
   Q = m . c . Δt = 3 . 380 . 60 = 68,400 J
4. Kết quả:
   Nhiệt lượng tiêu thụ để làm nóng miếng đồng là 68.4 kJ.

Các bài tập trên giúp chúng ta hiểu rõ cách tính toán và ứng dụng nhiệt lượng trong các tình huống thực tế. Điều này rất hữu ích không chỉ trong học tập mà còn trong đời sống hàng ngày khi xử lý các vấn đề liên quan đến nhiệt năng.