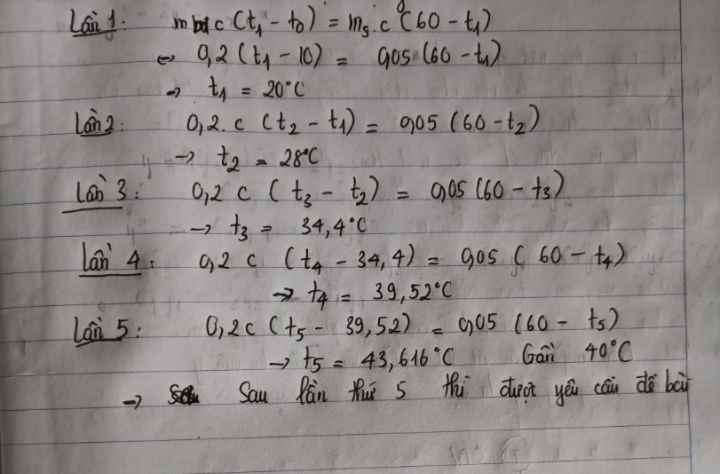Chủ đề nhiệt lượng của nước: Ứng dụng công thức tính nhiệt lượng của nước giúp chúng ta tối ưu hóa việc sử dụng năng lượng trong nhiều lĩnh vực như chế biến thực phẩm, gia nhiệt trong công nghiệp, và quản lý nhiệt độ trong y học. Hiểu và áp dụng đúng công thức sẽ mang lại hiệu quả cao và tiết kiệm chi phí.
Mục lục
Nhiệt Lượng Của Nước: Khái Niệm và Ứng Dụng
Nhiệt lượng của nước là một khái niệm quan trọng trong vật lý và hóa học, liên quan đến lượng nhiệt cần thiết để tăng nhiệt độ của một khối lượng nước nhất định. Hiểu biết về nhiệt lượng giúp chúng ta áp dụng trong nhiều lĩnh vực, từ đời sống hàng ngày đến công nghiệp.
1. Công Thức Tính Nhiệt Lượng
Công thức cơ bản để tính nhiệt lượng \(Q\) mà một vật thu vào hoặc toả ra là:
\[
Q = m \cdot c \cdot \Delta t
\]
- \(Q\): Nhiệt lượng (Joules, J)
- \(m\): Khối lượng của nước (kilogram, kg)
- \(c\): Nhiệt dung riêng của nước (\(c = 4186 \, \text{J/kg}^\circ \text{C}\))
- \(\Delta t\): Độ biến thiên nhiệt độ (\(^\circ \text{C}\))
2. Yếu Tố Ảnh Hưởng Đến Nhiệt Lượng Của Nước
Các yếu tố chính ảnh hưởng đến nhiệt lượng bao gồm:
- Khối lượng của nước: Khối lượng nước càng lớn, nhiệt lượng cần thiết để tăng nhiệt độ càng cao.
- Độ biến thiên nhiệt độ: Sự thay đổi nhiệt độ càng lớn thì nhiệt lượng cần thiết càng nhiều.
- Chất cấu tạo: Nhiệt dung riêng của nước là một trong những yếu tố quyết định lượng nhiệt mà nước cần để thay đổi nhiệt độ.
3. Ứng Dụng Của Nhiệt Lượng Trong Đời Sống
Nhiệt lượng của nước có nhiều ứng dụng thực tiễn, từ sinh hoạt hàng ngày đến công nghiệp:
- Trong sinh hoạt: Sử dụng để đun nước nấu ăn, tắm rửa, sưởi ấm, v.v.
- Trong công nghiệp: Được ứng dụng trong các hệ thống nhiệt, như lò hơi, tản nhiệt, và nhiều thiết bị khác.
- Trong y học: Nhiệt lượng được sử dụng để kiểm soát nhiệt độ cơ thể, trong các phương pháp điều trị bằng nhiệt.
4. Bài Tập Thực Hành
Dưới đây là một bài tập minh họa:
Giả sử bạn có 2 cốc nước, mỗi cốc chứa 0,5 kg nước. Nhiệt độ ban đầu của cả hai cốc là 25°C. Bạn muốn đun nóng cốc thứ nhất lên 50°C và cốc thứ hai lên 75°C. Hãy tính nhiệt lượng cần thiết cho mỗi cốc.
Lời giải:
| Cốc | \(\Delta t\) | Nhiệt lượng \(Q\) (J) |
|---|---|---|
| Cốc 1 | \(\Delta t = 50^\circ \text{C} - 25^\circ \text{C} = 25^\circ \text{C}\) | \(Q_1 = 0,5 \cdot 4186 \cdot 25 = 52325 \, \text{J}\) |
| Cốc 2 | \(\Delta t = 75^\circ \text{C} - 25^\circ \text{C} = 50^\circ \text{C}\) | \(Q_2 = 0,5 \cdot 4186 \cdot 50 = 104650 \, \text{J}\) |
Như vậy, để đun nóng 0,5 kg nước từ 25°C lên 50°C cần 52325 J, và từ 25°C lên 75°C cần 104650 J.
.jpg)
.png)
1. Khái Niệm Về Nhiệt Lượng
Nhiệt lượng là một dạng năng lượng được truyền từ vật này sang vật khác thông qua sự khác biệt về nhiệt độ. Khi một vật thể nhận nhiệt lượng, nhiệt độ của nó có xu hướng tăng lên, trong khi khi mất nhiệt lượng, nhiệt độ của nó có thể giảm xuống.
1.1. Định Nghĩa Nhiệt Lượng
Nhiệt lượng là năng lượng trao đổi giữa các hệ vật lý dưới dạng nhiệt. Nó được đo bằng đơn vị năng lượng, thường là joule (J). Khi hai vật có nhiệt độ khác nhau tiếp xúc, nhiệt lượng sẽ truyền từ vật có nhiệt độ cao hơn sang vật có nhiệt độ thấp hơn cho đến khi đạt được trạng thái cân bằng nhiệt.
1.2. Đơn Vị Đo Nhiệt Lượng
Đơn vị đo nhiệt lượng trong hệ SI là joule (J). Ngoài ra, calo (cal) cũng là một đơn vị phổ biến để đo nhiệt lượng, với 1 calo tương đương với 4.184 joule.
1.3. Công Thức Tính Nhiệt Lượng
Công thức cơ bản để tính nhiệt lượng là:
$$Q = mc\Delta t$$
- Q: Nhiệt lượng (J)
- m: Khối lượng của chất (kg)
- c: Nhiệt dung riêng của chất (J/kg.°C)
- Δt: Độ biến thiên nhiệt độ (°C)
Công thức này cho phép xác định nhiệt lượng cần thiết để tăng hoặc giảm nhiệt độ của một vật thể.
2. Các Yếu Tố Ảnh Hưởng Đến Nhiệt Lượng
Nhiệt lượng của một vật thể là lượng năng lượng cần thiết để thay đổi nhiệt độ của nó. Các yếu tố chính ảnh hưởng đến nhiệt lượng bao gồm:
- Khối lượng của vật thể (m): Khối lượng của vật thể tỉ lệ thuận với nhiệt lượng cần thiết để thay đổi nhiệt độ của nó. Khi khối lượng của vật thể tăng, nhiệt lượng cần thiết cũng tăng tương ứng. Ngược lại, khi khối lượng giảm, nhiệt lượng cần thiết cũng giảm.
- Độ tăng nhiệt độ (Δt): Sự biến đổi nhiệt độ của vật thể là yếu tố quan trọng ảnh hưởng đến nhiệt lượng. Độ tăng nhiệt độ càng lớn, nhiệt lượng hấp thụ càng cao. Điều này có nghĩa rằng, để đạt được một sự thay đổi nhiệt độ lớn, cần cung cấp nhiều nhiệt lượng hơn.
- Nhiệt dung riêng của chất liệu (c): Mỗi chất liệu có một nhiệt dung riêng khác nhau, đặc trưng cho khả năng hấp thụ nhiệt của nó. Chất liệu có nhiệt dung riêng lớn sẽ yêu cầu nhiều nhiệt lượng hơn để tăng nhiệt độ so với chất liệu có nhiệt dung riêng nhỏ.
Các yếu tố này tương tác với nhau theo công thức tính nhiệt lượng:
\[ Q = m \times c \times \Delta t \]
Trong đó:
- Q: Nhiệt lượng (J)
- m: Khối lượng của vật (kg)
- c: Nhiệt dung riêng của chất liệu (J/kg.K)
- Δt: Độ biến thiên nhiệt độ (°C hoặc K)
Như vậy, để tính toán nhiệt lượng cần thiết cho một sự thay đổi nhiệt độ cụ thể, ta cần xem xét đầy đủ các yếu tố này và đảm bảo tính chính xác trong việc xác định chúng.

4. Các Phương Pháp Đo Lường Nhiệt Lượng
Đo lường nhiệt lượng là một phần quan trọng trong nghiên cứu và ứng dụng nhiệt học. Các phương pháp đo lường nhiệt lượng có thể được phân thành hai loại chính: phương pháp trực tiếp và phương pháp gián tiếp.
4.1. Phương Pháp Trực Tiếp
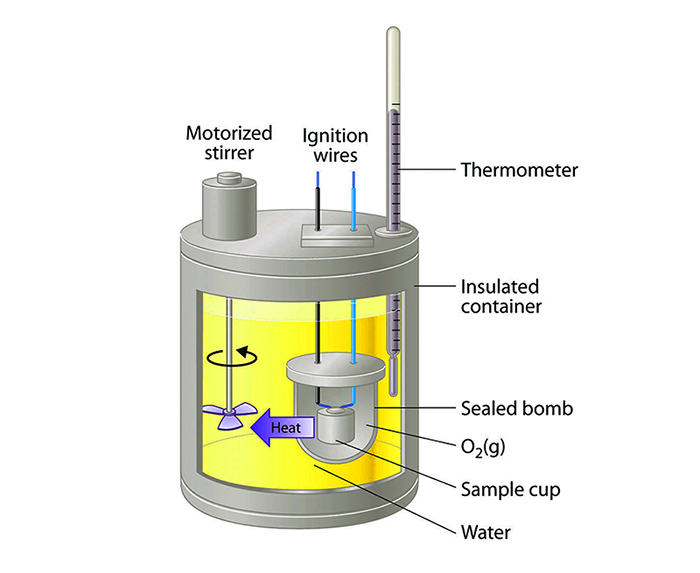
Phương pháp trực tiếp đo lường nhiệt lượng thông qua việc sử dụng các thiết bị đo nhiệt lượng như máy đo nhiệt lượng (calorimeter). Các bước thực hiện như sau:
- Chuẩn bị mẫu: Mẫu cần đo được đưa vào bên trong máy đo nhiệt lượng.
- Thực hiện phép đo: Máy đo nhiệt lượng sẽ ghi nhận sự thay đổi nhiệt độ của mẫu trong một môi trường cách nhiệt.
- Tính toán nhiệt lượng: Sử dụng công thức \( Q = m \cdot c \cdot \Delta t \), trong đó:
- Q: Nhiệt lượng cần đo (Joules).
- m: Khối lượng của mẫu (kg).
- c: Nhiệt dung riêng của mẫu (J/kg·K).
- \(\Delta t\): Độ biến thiên nhiệt độ (K).
4.2. Phương Pháp Gián Tiếp
Phương pháp gián tiếp đo lường nhiệt lượng bằng cách suy ra từ các đại lượng khác như công suất điện, thời gian hoặc cường độ dòng điện. Dưới đây là một số phương pháp phổ biến:
- Phương pháp điện trở: Sử dụng một điện trở để chuyển hóa điện năng thành nhiệt năng và đo lường nhiệt lượng dựa trên công suất điện và thời gian. Công thức tính nhiệt lượng trong trường hợp này là \( Q = I^2 \cdot R \cdot t \), trong đó:
- I: Cường độ dòng điện (Amperes).
- R: Điện trở (Ohms).
- t: Thời gian (seconds).
- Phương pháp sử dụng năng suất tỏa nhiệt của nhiên liệu: Khi đốt cháy nhiên liệu, nhiệt lượng tỏa ra có thể được tính bằng công thức \( Q = q \cdot m \), trong đó:
- Q: Nhiệt lượng tỏa ra (Joules).
- q: Năng suất tỏa nhiệt của nhiên liệu (J/kg).
- m: Khối lượng nhiên liệu (kg).
Hai phương pháp trên đều có những ưu điểm và hạn chế riêng. Phương pháp trực tiếp thường cho kết quả chính xác hơn nhưng đòi hỏi thiết bị phức tạp và thời gian thực hiện lâu hơn. Phương pháp gián tiếp linh hoạt hơn nhưng có thể gặp sai số nếu không kiểm soát tốt các yếu tố ảnh hưởng.
XEM THÊM:
5. Ví Dụ Thực Tế Về Nhiệt Lượng
Dưới đây là một số ví dụ thực tế về nhiệt lượng được sử dụng trong cuộc sống hàng ngày và trong các lĩnh vực khác nhau:
5.1. Tính Nhiệt Lượng Của Một Vật Cụ Thể
Giả sử chúng ta cần tính nhiệt lượng để đun sôi nước trong một ấm nhôm. Để đun sôi 2 lít nước từ 20°C đến 100°C trong ấm nhôm có khối lượng 0.5 kg, chúng ta sử dụng các công thức sau:
- Nhiệt lượng để làm nóng ấm nhôm:
- \( Q_{\text{ấm}} = m_{\text{ấm}} \times c_{\text{ấm}} \times \Delta t \)
- \( = 0.5 \times 880 \times (100 - 20) = 35200 \, J \)
- Nhiệt lượng để làm nóng nước:
- \( Q_{\text{nước}} = m_{\text{nước}} \times c_{\text{nước}} \times \Delta t \)
- \( = 2 \times 4200 \times (100 - 20) = 672000 \, J \)
- Tổng nhiệt lượng cần để đun sôi nước:
- \( Q_{\text{tổng}} = Q_{\text{ấm}} + Q_{\text{nước}} \)
- \( = 35200 + 672000 = 707200 \, J \)
5.2. So Sánh Nhiệt Lượng Giữa Các Chất Liệu Khác Nhau
So sánh nhiệt lượng cần để đun nóng nước và sắt từ 10°C đến 100°C:
- Nhiệt lượng để đun nóng 3kg nước:
- \( Q_{\text{nước}} = m_{\text{nước}} \times c_{\text{nước}} \times \Delta t \)
- \( = 3 \times 4200 \times (100 - 10) = 1.134.000 \, J \)
- Nhiệt lượng để đun nóng 2kg sắt:
- \( Q_{\text{sắt}} = m_{\text{sắt}} \times c_{\text{sắt}} \times \Delta t \)
- \( = 2 \times 460 \times (100 - 10) = 82.800 \, J \)
Như vậy, nước cần nhiệt lượng lớn hơn rất nhiều so với sắt để tăng cùng một lượng nhiệt độ, điều này cho thấy sự khác biệt về nhiệt dung riêng giữa các chất liệu.
5.3. Ứng Dụng Thực Tiễn
Ví dụ, trong công nghiệp rèn, khi một thợ rèn nhúng một con dao thép nóng đỏ vào bể nước để làm nguội. Giả sử con dao có khối lượng 2.5 kg, nhiệt độ ban đầu 900°C, và nước trong bể có thể tích 200 lít ở nhiệt độ 27°C. Nhiệt lượng trao đổi có thể tính như sau:
- Nhiệt lượng do con dao tỏa ra:
- \( Q_{\text{dao}} = m_{\text{dao}} \times c_{\text{thép}} \times \Delta t \)
- \( = 2.5 \times 460 \times (900 - t) \)
- Nhiệt lượng do nước thu vào:
- \( Q_{\text{nước}} = m_{\text{nước}} \times c_{\text{nước}} \times \Delta t \)
- \( = 200 \times 4200 \times (t - 27) \)
- Khi cân bằng nhiệt:
- \( Q_{\text{dao}} = Q_{\text{nước}} \)
- Giải phương trình để tìm nhiệt độ cân bằng \( t \):
- \( 2.5 \times 460 \times (900 - t) = 200 \times 4200 \times (t - 27) \)
- \( t \approx 28.2°C \)

6. Bài Tập Thực Hành Về Nhiệt Lượng
6.1. Bài Tập Tính Nhiệt Lượng
Dưới đây là một số bài tập thực hành giúp bạn hiểu rõ hơn về cách tính nhiệt lượng:
-
Một ấm nhôm có khối lượng 0,3 kg chứa 2 lít nước. Tính nhiệt lượng cần thiết để đun nước từ 15°C đến 100°C.
Giải:
- Nhiệt lượng cần cung cấp cho ấm nhôm:
\( Q_1 = m_1 \cdot c_1 \cdot \Delta t = 0,3 \, \text{kg} \cdot 880 \, \text{J/kg} \cdot \text{K} \cdot (100 - 15) \, \text{K} = 22440 \, \text{J} \)
- Nhiệt lượng cần cung cấp cho nước:
\( Q_2 = m_2 \cdot c_2 \cdot \Delta t = 2 \, \text{kg} \cdot 4200 \, \text{J/kg} \cdot \text{K} \cdot (100 - 15) \, \text{K} = 714000 \, \text{J} \)
- Tổng nhiệt lượng cần thiết:
\( Q = Q_1 + Q_2 = 22440 \, \text{J} + 714000 \, \text{J} = 736440 \, \text{J} \)
- Nhiệt lượng cần cung cấp cho ấm nhôm:
Một khối lượng nước 25 kg thu được một nhiệt lượng 1050 kJ thì nóng lên tới 30°C. Tính nhiệt độ ban đầu của nước.
Giải:
- Gọi \( t_1 \) là nhiệt độ ban đầu của nước.
\( Q = m \cdot c \cdot (t_2 - t_1) \)
\( 1050 \, \text{kJ} = 25 \, \text{kg} \cdot 4200 \, \text{J/kg} \cdot \text{K} \cdot (30 \, \text{°C} - t_1) \)
\( t_1 = 30 - \frac{1050 \times 10^3}{25 \cdot 4200} = 20 \, \text{°C} \)
- Gọi \( t_1 \) là nhiệt độ ban đầu của nước.
6.2. Bài Tập Ứng Dụng Nhiệt Lượng
Những bài tập sau giúp bạn áp dụng kiến thức nhiệt lượng vào thực tế:
-
Đặt một ấm nhôm có khối lượng 400 g chứa 2 lít nước sôi 100°C vào phòng có nhiệt độ 27°C. Sau 1 giờ 30 phút, nhiệt độ của nước trong ấm là 27°C. Tính nhiệt lượng mà không khí trong phòng đã nhận.
Giải:
- Nhiệt lượng nước tỏa ra:
\( Q_1 = m_1 \cdot c_1 \cdot \Delta t = 2 \, \text{kg} \cdot 4200 \, \text{J/kg} \cdot \text{K} \cdot (100 - 27) \, \text{K} = 613200 \, \text{J} \)
- Nhiệt lượng ấm nhôm tỏa ra:
\( Q_2 = m_2 \cdot c_2 \cdot \Delta t = 0,4 \, \text{kg} \cdot 880 \, \text{J/kg} \cdot \text{K} \cdot (100 - 27) \, \text{K} = 25704 \, \text{J} \)
- Tổng nhiệt lượng không khí nhận:
\( Q = Q_1 + Q_2 = 613200 \, \text{J} + 25704 \, \text{J} = 638904 \, \text{J} \)
- Nhiệt lượng nước tỏa ra:
Tại xưởng rèn, một thợ rèn nhúng con dao bằng thép có khối lượng 2,5 kg đang nóng đỏ ở nhiệt độ 900°C vào bể nước lạnh có thể tích 200 lít và nhiệt độ 27°C. Bỏ qua sự truyền nhiệt cho thành bể và môi trường xung quanh. Tính nhiệt độ của con dao khi có sự cân bằng nhiệt.
Giải:
- Nhiệt lượng do con dao thép tỏa ra:
\( Q_1 = m_1 \cdot c_1 \cdot (t_1 - t) \)
- Nhiệt lượng do nước thu vào:
\( Q_2 = m_2 \cdot c_2 \cdot (t - t_2) \)
- Vì bỏ qua sự trao đổi nhiệt với môi trường nên \( Q_1 = Q_2 \):
\( m_1 \cdot c_1 \cdot (t_1 - t) = m_2 \cdot c_2 \cdot (t - t_2) \)
\( (2,5 \cdot 460 \cdot 900) + (200 \cdot 4200 \cdot 27) = (2,5 \cdot 460) + (200 \cdot 4200) \cdot t \)
\( t \approx 28,2°C \)
- Nhiệt lượng do con dao thép tỏa ra: