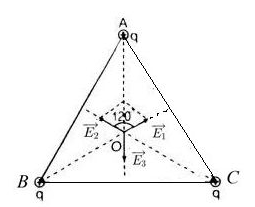
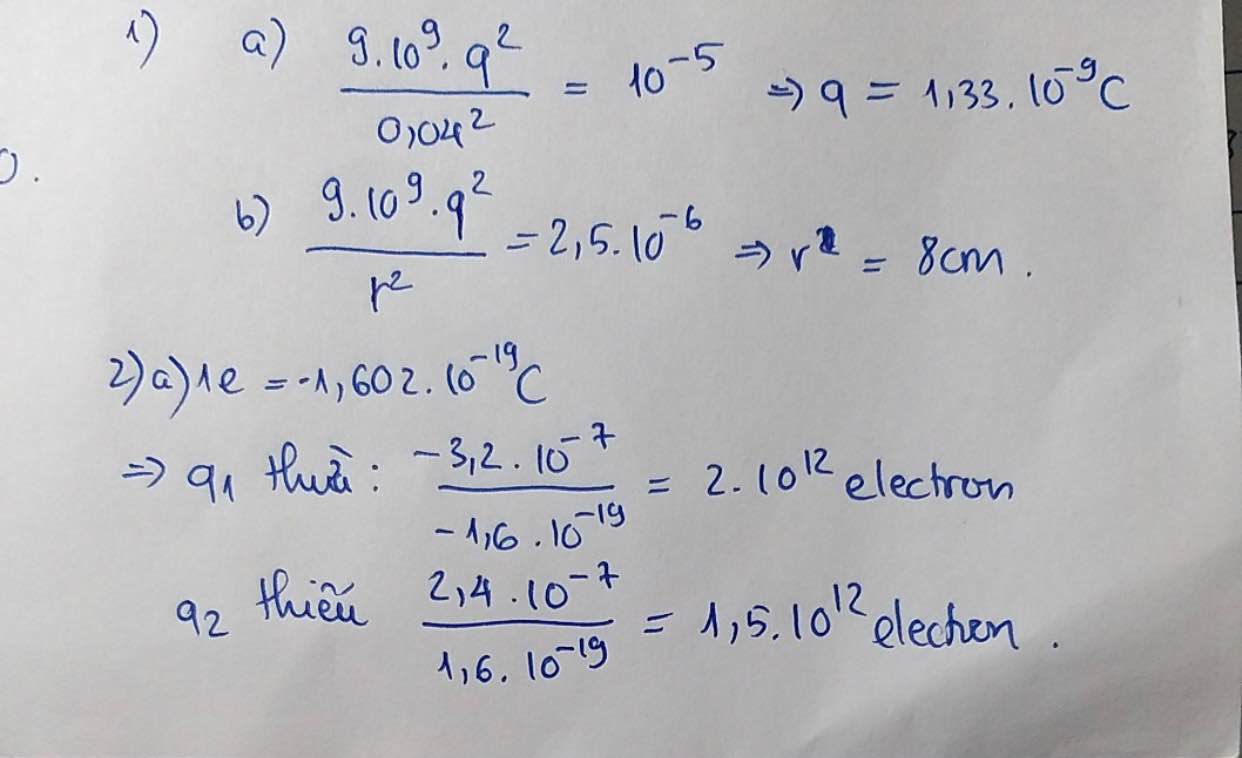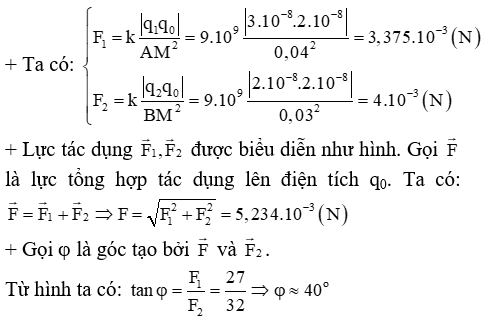Chủ đề điện tích q bằng bao nhiêu: Điện tích Q là một khái niệm quan trọng trong vật lý học, ảnh hưởng đến nhiều hiện tượng và ứng dụng thực tế. Bài viết này sẽ cung cấp cho bạn hiểu biết chi tiết về cách tính toán điện tích, các định luật liên quan, và ứng dụng của điện tích trong cuộc sống hàng ngày.
Mục lục
Điện Tích \(q\) Bằng Bao Nhiêu?
Trong vật lý học, điện tích \(q\) là một đại lượng vật lý biểu hiện tính chất của các hạt mang điện, có thể là điện tích dương hoặc âm. Điện tích được ký hiệu bằng chữ cái thường \(q\) và đơn vị đo là Coulomb (C).
1. Đơn Vị Đo Điện Tích
Điện tích được đo bằng đơn vị Coulomb (C) trong hệ đo lường quốc tế (SI). Các quy đổi đơn vị phổ biến bao gồm:
- 1 Coulomb = \(10^9\) Nanocoulomb (nC)
- 1 Coulomb = \(10^6\) Microcoulomb (µC)
- 1 Coulomb = \(1.000\) Millicoulomb (mC)
2. Công Thức Tính Điện Tích \(q\)
Điện tích của một vật có thể được tính bằng công thức:
\[
q = \pm n \times e
\]
Trong đó:
- \(q\) là điện tích của vật
- \(n\) là số nguyên dương, biểu thị số lượng hạt cơ bản
- \(e\) là điện tích của một electron, có giá trị xấp xỉ \(1.602 \times 10^{-19}\) C
3. Các Định Luật Liên Quan Đến Điện Tích
Các định luật quan trọng liên quan đến điện tích bao gồm:
- Định luật bảo toàn điện tích: Trong một hệ kín, tổng điện tích luôn được bảo toàn.
- Định luật Coulomb: Lực hút hoặc đẩy giữa hai điện tích tỉ lệ thuận với tích của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
4. Ứng Dụng Của Điện Tích
Điện tích \(q\) có nhiều ứng dụng trong thực tiễn, từ việc tạo ra dòng điện trong các mạch điện tử cho đến ứng dụng trong công nghệ bán dẫn và vật liệu dẫn điện.
5. Kết Luận
Điện tích là một khái niệm cơ bản trong vật lý, liên quan đến nhiều hiện tượng và ứng dụng thực tế. Việc hiểu rõ về điện tích giúp chúng ta nắm bắt được các nguyên lý hoạt động của các thiết bị điện tử và các hiện tượng điện từ trong đời sống.
.png)
1. Khái Niệm Về Điện Tích
Điện tích là một đại lượng vật lý cơ bản biểu hiện tính chất của các hạt hạ nguyên tử, như electron và proton. Điện tích có thể là dương hoặc âm, và đại lượng này quyết định các lực tương tác giữa các hạt.
Trong hệ đo lường quốc tế (SI), điện tích được đo bằng đơn vị Coulomb (C). Một điện tích dương và một điện tích âm sẽ hút nhau, trong khi hai điện tích cùng dấu sẽ đẩy nhau, tạo ra các hiện tượng điện trường.
- Điện tích dương: Được tạo ra bởi sự mất mát của electron.
- Điện tích âm: Được tạo ra bởi sự thừa thãi của electron.
Công thức cơ bản để tính điện tích được định nghĩa là:
\[
q = n \times e
\]
Trong đó:
- \(q\) là điện tích.
- \(n\) là số nguyên dương, biểu thị số lượng hạt.
- \(e\) là điện tích cơ bản, có giá trị xấp xỉ \(1.602 \times 10^{-19}\) Coulomb.
Điện tích là yếu tố cơ bản trong việc hiểu các hiện tượng điện từ, từ hoạt động của các mạch điện đơn giản đến các ứng dụng phức tạp như trong công nghệ bán dẫn.
2. Công Thức Tính Điện Tích Q
Công thức cơ bản để tính điện tích \(q\) là:
\[
q = n \times e
\]
Trong đó:
- \(q\) là điện tích của vật (đơn vị: Coulomb - C).
- \(n\) là số hạt điện tích (nguyên dương hoặc âm).
- \(e\) là điện tích cơ bản của một electron, với giá trị xấp xỉ \(1.602 \times 10^{-19}\) C.
Để hiểu rõ hơn, bạn có thể xem xét trường hợp một vật có \(n\) electron. Khi đó, điện tích của vật sẽ là \(q = -n \times e\) (dấu âm thể hiện điện tích âm do electron mang).
Công Thức Trong Các Trường Hợp Cụ Thể
Các trường hợp khác nhau của điện tích được xác định bằng các công thức đặc biệt:
- Đối với một hạt đơn lẻ: \(q = n \times e\)
- Đối với một đám mây hạt: \(q = \sigma \times A\) với \(\sigma\) là mật độ điện tích và \(A\) là diện tích bề mặt.
Công Thức Điện Tích Trong Điện Trường
Trong một điện trường, lực tác động lên một điện tích \(q\) được tính bằng công thức:
\[
F = q \times E
\]
Trong đó:
- \(F\) là lực điện tác dụng lên điện tích (đơn vị: Newton - N).
- \(E\) là cường độ điện trường (đơn vị: Volt trên mét - V/m).
Công thức này giúp bạn hiểu rõ mối quan hệ giữa điện tích và lực trong một điện trường, ứng dụng rộng rãi trong các bài toán điện từ và các lĩnh vực công nghệ cao.

3. Định Luật Liên Quan Đến Điện Tích
Điện tích tuân theo nhiều định luật quan trọng trong vật lý, giúp chúng ta hiểu rõ hơn về cách các hạt mang điện tương tác và tác động lẫn nhau.
3.1. Định Luật Coulomb
Định luật Coulomb mô tả lực giữa hai điện tích điểm, được xác định bằng công thức:
\[
F = k \cdot \frac{|q_1 \cdot q_2|}{r^2}
\]
Trong đó:
- \(F\) là lực tương tác giữa hai điện tích (đơn vị: Newton - N).
- \(q_1\) và \(q_2\) là hai điện tích (đơn vị: Coulomb - C).
- \(r\) là khoảng cách giữa hai điện tích (đơn vị: mét - m).
- \(k\) là hằng số Coulomb, giá trị xấp xỉ \(8.99 \times 10^9 \, N \cdot m^2/C^2\).
Định luật này cho thấy lực tương tác tỉ lệ thuận với tích của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
3.2. Định Luật Bảo Toàn Điện Tích
Định luật bảo toàn điện tích phát biểu rằng tổng điện tích trong một hệ cô lập là không đổi, tức là điện tích không thể tự sinh ra hoặc mất đi, chỉ có thể truyền từ vật này sang vật khác.
- Ví dụ: Khi một vật trung hòa bị mất electron, nó sẽ trở thành vật mang điện tích dương, và điện tích âm sẽ được chuyển sang vật khác.
Định luật này là cơ sở cho nhiều hiện tượng trong điện học, chẳng hạn như trong các quá trình phóng điện và cảm ứng điện.
3.3. Định Luật Gauss
Định luật Gauss là một trong bốn phương trình Maxwell, mô tả mối quan hệ giữa điện tích và điện trường sinh ra bởi điện tích đó. Công thức của định luật Gauss là:
\[
\oint_{S} \mathbf{E} \cdot d\mathbf{A} = \frac{q_{\text{in}}}{\epsilon_0}
\]
Trong đó:
- \(\mathbf{E}\) là vectơ cường độ điện trường.
- \(d\mathbf{A}\) là vectơ diện tích của mặt kín \(S\).
- \(q_{\text{in}}\) là tổng điện tích bao quanh bởi mặt kín \(S\).
- \(\epsilon_0\) là hằng số điện môi trong chân không, giá trị xấp xỉ \(8.85 \times 10^{-12} \, C^2/N \cdot m^2\).
Định luật Gauss giúp tính toán cường độ điện trường trong các hệ có tính đối xứng cao, như hình cầu hoặc hình trụ.

4. Ứng Dụng Thực Tiễn Của Điện Tích
Điện tích đóng vai trò quan trọng trong nhiều ứng dụng thực tiễn, từ các thiết bị điện tử cho đến các công nghệ tiên tiến trong y học và công nghiệp.
4.1. Ứng Dụng Trong Các Thiết Bị Điện Tử
- Linh kiện điện tử: Điện tích là cơ sở hoạt động của các linh kiện như tụ điện, transistor, và diốt, các thành phần này tạo nên các mạch điện tử cơ bản.
- Pin và ắc quy: Nguyên lý hoạt động của pin dựa trên sự di chuyển của các điện tích giữa các cực âm và dương, cung cấp năng lượng cho các thiết bị điện tử.
4.2. Ứng Dụng Trong Y Học
- Điện tâm đồ (ECG): Sử dụng điện tích để đo hoạt động điện của tim, giúp chẩn đoán các vấn đề liên quan đến tim mạch.
- Điện não đồ (EEG): Đo điện tích trên da đầu để phân tích hoạt động của não, hỗ trợ trong việc chẩn đoán các rối loạn thần kinh.
4.3. Ứng Dụng Trong Công Nghiệp
- Sơn tĩnh điện: Sử dụng điện tích để bám dính sơn lên bề mặt kim loại một cách đồng đều và bền vững.
- Xử lý nước thải: Sử dụng điện tích để loại bỏ các hạt bụi và tạp chất trong nước, cải thiện chất lượng nước thải.
4.4. Ứng Dụng Trong Công Nghệ Năng Lượng
- Pin mặt trời: Điện tích sinh ra từ các tế bào quang điện khi tiếp xúc với ánh sáng mặt trời, được chuyển hóa thành năng lượng điện.
- Máy phát điện: Điện tích được tạo ra khi có sự chuyển động của các electron trong dây dẫn, tạo ra dòng điện phục vụ nhu cầu sử dụng năng lượng.

5. Cách Đo Và Tính Điện Tích Q
Điện tích \( Q \) là một đại lượng vật lý cơ bản, được đo lường và tính toán bằng nhiều phương pháp khác nhau trong vật lý. Dưới đây là các bước cơ bản để đo và tính điện tích \( Q \).
5.1. Cách Đo Điện Tích Bằng Thiết Bị
- Điện kế: Sử dụng điện kế để đo điện tích bằng cách xác định độ lệch của kim điện kế khi tiếp xúc với vật mang điện.
- Bình nghiệm Coulomb: Sử dụng bình nghiệm Coulomb để đo lực tương tác giữa các điện tích, từ đó tính toán được giá trị của \( Q \).
5.2. Công Thức Tính Điện Tích Q
Điện tích \( Q \) có thể được tính toán thông qua công thức cơ bản sau:
\[
Q = I \times t
\]
Trong đó:
- \( Q \): Điện tích (đơn vị Coulomb)
- \( I \): Cường độ dòng điện (đơn vị Ampere)
- \( t \): Thời gian (đơn vị giây)
5.3. Bước Tính Điện Tích Trong Thực Tế
- Chuẩn bị dụng cụ đo: Sử dụng các dụng cụ đo như ampe kế và đồng hồ đo thời gian để xác định \( I \) và \( t \).
- Thực hiện đo đạc: Đo cường độ dòng điện \( I \) chạy qua mạch trong thời gian \( t \).
- Tính toán: Áp dụng công thức \( Q = I \times t \) để tính toán điện tích \( Q \).
- Kiểm tra và ghi nhận: So sánh kết quả với giá trị mong đợi và ghi nhận kết quả đo.
Các phương pháp trên giúp đảm bảo việc đo và tính điện tích \( Q \) được thực hiện một cách chính xác và hiệu quả.