Chủ đề công thức tính góc khúc xạ: Công thức tính góc khúc xạ là kiến thức quan trọng trong vật lý, giúp hiểu rõ hiện tượng khúc xạ ánh sáng khi truyền qua các môi trường khác nhau. Bài viết này sẽ hướng dẫn chi tiết cách tính toán, giải thích ý nghĩa và phân tích các ứng dụng thực tế của công thức, giúp bạn nắm vững và áp dụng hiệu quả trong học tập cũng như cuộc sống.
Mục lục
Công Thức Tính Góc Khúc Xạ
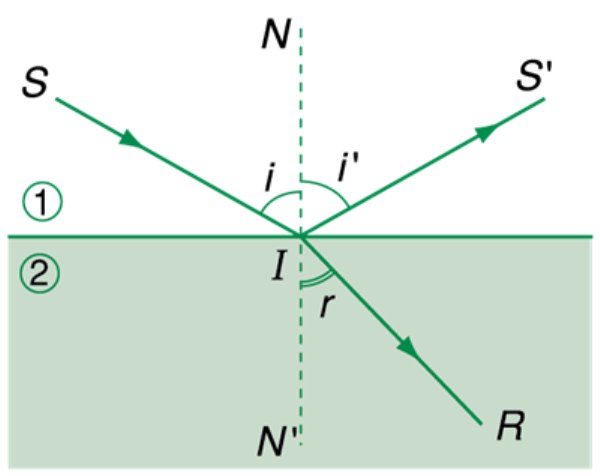
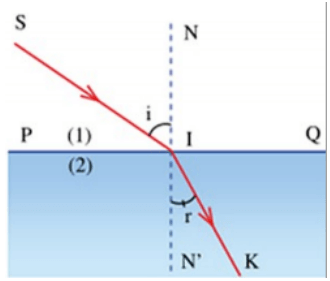
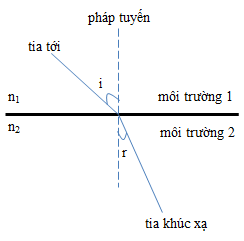
Khúc xạ ánh sáng là hiện tượng khi một tia sáng truyền qua mặt phân cách giữa hai môi trường trong suốt có chiết suất khác nhau, nó sẽ bị lệch hướng. Góc khúc xạ là góc tạo bởi tia khúc xạ và pháp tuyến của mặt phân cách tại điểm tia sáng tiếp xúc.
1. Định luật khúc xạ ánh sáng
Theo định luật khúc xạ ánh sáng, với hai môi trường trong suốt cố định, tỉ số giữa sin của góc tới \( i \) và sin của góc khúc xạ \( r \) là một hằng số, được gọi là chiết suất tỉ đối của hai môi trường.
- Công thức:
\[
\frac{\sin(i)}{\sin(r)} = n_{21}
\]
trong đó:
- \( i \): Góc tới (góc tạo bởi tia tới và pháp tuyến)
- \( r \): Góc khúc xạ (góc tạo bởi tia khúc xạ và pháp tuyến)
- \( n_{21} \): Chiết suất tỉ đối của môi trường 2 so với môi trường 1
2. Công thức chiết suất tuyệt đối
Chiết suất tuyệt đối là tỉ số giữa tốc độ ánh sáng trong chân không và tốc độ ánh sáng trong môi trường đó.
- Công thức:
\[
n = \frac{c}{v}
\]
trong đó:
- \( n \): Chiết suất tuyệt đối của môi trường
- \( c \): Tốc độ ánh sáng trong chân không (khoảng \( 3 \times 10^8 \) m/s)
- \( v \): Tốc độ ánh sáng trong môi trường đang xét
3. Ứng dụng của hiện tượng khúc xạ ánh sáng
Hiện tượng khúc xạ ánh sáng có nhiều ứng dụng trong cuộc sống hàng ngày, từ việc chế tạo kính mắt, ống kính máy ảnh cho đến các thiết bị quang học khác. Khả năng điều chỉnh đường truyền ánh sáng thông qua việc thay đổi góc tới và chất liệu của các môi trường giúp tối ưu hóa hiệu suất của các thiết bị này.
4. Bài tập áp dụng
Dưới đây là một số bài tập giúp củng cố kiến thức về khúc xạ ánh sáng:
- Một tia sáng chiếu từ không khí vào nước với góc tới \( i = 30^\circ \). Tính góc khúc xạ \( r \) biết chiết suất của nước là \( n = 1.33 \).
- Xác định góc tới khi góc khúc xạ \( r = 25^\circ \) và tia sáng truyền từ thủy tinh (n = 1.5) vào không khí.
Thông qua việc hiểu rõ về góc khúc xạ và các công thức liên quan, bạn có thể dễ dàng giải quyết các bài toán về hiện tượng khúc xạ ánh sáng trong môn Vật lý.

.png)
I. Giới thiệu về hiện tượng khúc xạ ánh sáng
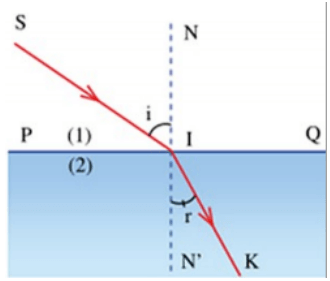
Khúc xạ ánh sáng là một hiện tượng vật lý quan trọng, xảy ra khi ánh sáng truyền từ môi trường này sang môi trường khác có chiết suất khác nhau. Hiện tượng này làm cho tia sáng bị thay đổi phương hướng tại bề mặt tiếp xúc giữa hai môi trường.
Cụ thể, khi ánh sáng truyền từ môi trường có chiết suất thấp (như không khí) vào môi trường có chiết suất cao hơn (như nước hoặc thủy tinh), tia sáng sẽ bị bẻ cong về phía pháp tuyến. Ngược lại, khi ánh sáng truyền từ môi trường có chiết suất cao sang môi trường có chiết suất thấp, tia sáng sẽ bị bẻ cong ra xa pháp tuyến.
Hiện tượng khúc xạ ánh sáng có thể được giải thích bằng định luật Snell-Descartes, một trong những định luật cơ bản trong quang học. Định luật này nêu rõ mối quan hệ giữa góc tới \( i \) và góc khúc xạ \( r \) thông qua công thức:
\[
\frac{\sin(i)}{\sin(r)} = \frac{n_2}{n_1}
\]
Trong đó:
- \( i \) là góc tới, được tạo bởi tia tới và pháp tuyến.
- \( r \) là góc khúc xạ, được tạo bởi tia khúc xạ và pháp tuyến.
- \( n_1 \) và \( n_2 \) lần lượt là chiết suất của môi trường thứ nhất và thứ hai.
Khúc xạ ánh sáng có nhiều ứng dụng thực tế, từ việc chế tạo các thiết bị quang học như kính lúp, kính hiển vi, kính viễn vọng, đến các ứng dụng trong đời sống hàng ngày như sự xuất hiện của cầu vồng hay hiện tượng ảo ảnh. Việc hiểu rõ và nắm vững hiện tượng khúc xạ sẽ giúp chúng ta áp dụng nó một cách hiệu quả trong nhiều lĩnh vực khác nhau.
II. Định luật và công thức tính góc khúc xạ
Định luật khúc xạ ánh sáng là nền tảng quan trọng trong việc hiểu và tính toán hiện tượng khúc xạ. Định luật này, được biết đến là định luật Snell-Descartes, mô tả mối quan hệ giữa góc tới và góc khúc xạ khi tia sáng truyền từ môi trường này sang môi trường khác.
Theo định luật Snell-Descartes, tỉ số giữa sin của góc tới \( i \) và sin của góc khúc xạ \( r \) bằng tỉ số giữa chiết suất của môi trường khúc xạ \( n_2 \) và chiết suất của môi trường mà tia sáng truyền tới \( n_1 \). Công thức này được biểu diễn như sau:
\[
\frac{\sin(i)}{\sin(r)} = \frac{n_2}{n_1}
\]
Trong đó:
- \( i \) là góc tới, là góc giữa tia tới và pháp tuyến tại điểm tới.
- \( r \) là góc khúc xạ, là góc giữa tia khúc xạ và pháp tuyến tại điểm khúc xạ.
- \( n_1 \) là chiết suất của môi trường thứ nhất, nơi tia sáng ban đầu truyền tới.
- \( n_2 \) là chiết suất của môi trường thứ hai, nơi tia sáng khúc xạ.
Nếu chiết suất của môi trường thứ hai lớn hơn chiết suất của môi trường thứ nhất (\( n_2 > n_1 \)), góc khúc xạ \( r \) sẽ nhỏ hơn góc tới \( i \), và ngược lại. Điều này giải thích tại sao khi nhìn từ không khí vào nước, vật thể dưới nước có vẻ gần hơn so với thực tế.
Công thức này không chỉ là cơ sở lý thuyết mà còn được ứng dụng rộng rãi trong các ngành như quang học, vật lý, và công nghệ. Chẳng hạn, nó được sử dụng trong việc thiết kế các loại thấu kính quang học, tính toán và điều chỉnh hướng của ánh sáng trong các hệ thống quang học phức tạp, và thậm chí trong việc chế tạo các thiết bị y tế như kính áp tròng.
Để hiểu rõ hơn về cách áp dụng công thức tính góc khúc xạ, chúng ta có thể thực hành với các bài toán tính toán cụ thể, từ đó nắm vững hơn quy luật và ứng dụng của định luật Snell-Descartes trong thực tế.

III. Phân tích chuyên sâu về chiết suất
Chiết suất là một đại lượng vật lý quan trọng, biểu thị mức độ bẻ cong của tia sáng khi nó truyền qua các môi trường khác nhau. Chiết suất của một môi trường được xác định bằng tỉ số giữa tốc độ ánh sáng trong chân không và tốc độ ánh sáng trong môi trường đó. Công thức tổng quát để tính chiết suất là:
\[
n = \frac{c}{v}
\]
Trong đó:
- \( n \): Chiết suất của môi trường.
- \( c \): Tốc độ ánh sáng trong chân không, xấp xỉ \( 3 \times 10^8 \) m/s.
- \( v \): Tốc độ ánh sáng trong môi trường đang xét.
Một môi trường có chiết suất cao hơn sẽ làm giảm tốc độ ánh sáng nhiều hơn, và do đó, ánh sáng sẽ bị bẻ cong nhiều hơn khi truyền qua môi trường đó. Chiết suất phụ thuộc vào tính chất vật lý của môi trường, như mật độ, thành phần hóa học, và đặc biệt là tần số của ánh sáng. Vì vậy, chiết suất của cùng một môi trường có thể thay đổi theo bước sóng của ánh sáng.
Ví dụ, chiết suất của nước đối với ánh sáng nhìn thấy là khoảng 1.33, có nghĩa là ánh sáng truyền trong nước với tốc độ chậm hơn so với trong chân không. Ngược lại, chiết suất của thủy tinh có thể nằm trong khoảng từ 1.5 đến 1.9 tùy thuộc vào loại thủy tinh, điều này giải thích tại sao thủy tinh thường được sử dụng trong các thiết bị quang học như kính hiển vi và kính viễn vọng.
Chiết suất không chỉ là một khái niệm lý thuyết mà còn có ứng dụng thực tiễn rất lớn. Trong thiết kế các hệ thống quang học, việc chọn lựa vật liệu có chiết suất phù hợp là vô cùng quan trọng để đảm bảo hiệu suất tối ưu. Ví dụ, kính có chiết suất cao hơn được sử dụng để tạo ra các thấu kính hội tụ mạnh hơn, giúp cải thiện chất lượng hình ảnh trong các thiết bị như máy ảnh và ống nhòm.
Hơn nữa, sự thay đổi của chiết suất theo bước sóng là nguyên nhân gây ra hiện tượng tán sắc, tức là sự phân tách của ánh sáng trắng thành các màu sắc khác nhau khi đi qua lăng kính. Điều này không chỉ mang lại những hiệu ứng quang học thú vị mà còn là cơ sở cho nhiều kỹ thuật phân tích quang phổ trong khoa học.
Như vậy, việc hiểu rõ chiết suất và các yếu tố ảnh hưởng đến nó là rất quan trọng trong nhiều lĩnh vực từ nghiên cứu khoa học đến ứng dụng công nghệ. Khả năng điều chỉnh và kiểm soát chiết suất của các vật liệu cho phép con người phát triển các thiết bị quang học với hiệu suất cao và độ chính xác vượt trội.
IV. Bài tập và lời giải chi tiết
Dưới đây là một số bài tập về khúc xạ ánh sáng giúp bạn củng cố kiến thức về công thức tính góc khúc xạ. Mỗi bài tập đều được kèm theo lời giải chi tiết, giúp bạn hiểu rõ hơn về cách áp dụng định luật Snell-Descartes và các khái niệm liên quan.
-
Bài tập 1: Một tia sáng truyền từ không khí vào nước với góc tới \( i = 30^\circ \). Biết chiết suất của không khí là \( n_1 = 1 \) và của nước là \( n_2 = 1.33 \). Tính góc khúc xạ \( r \).
Lời giải:
Áp dụng định luật Snell-Descartes:
\[
\frac{\sin(i)}{\sin(r)} = \frac{n_2}{n_1}
\]
\[
\sin(r) = \frac{\sin(30^\circ) \times 1}{1.33} = \frac{0.5}{1.33} \approx 0.376
\]Vậy \( r = \sin^{-1}(0.376) \approx 22^\circ \).
-
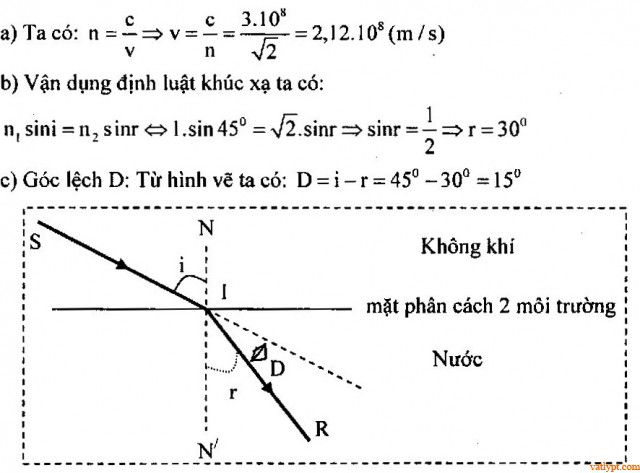
Bài tập 2: Một tia sáng truyền từ thủy tinh có chiết suất \( n_2 = 1.5 \) ra không khí với góc tới \( i = 45^\circ \). Tính góc khúc xạ \( r \) trong không khí.
Lời giải:
Áp dụng định luật Snell-Descartes:
\[
\frac{\sin(i)}{\sin(r)} = \frac{n_1}{n_2}
\]
\[
\sin(r) = \frac{\sin(45^\circ) \times 1}{1.5} = \frac{0.707}{1.5} \approx 0.471
\]Vậy \( r = \sin^{-1}(0.471) \approx 28^\circ \).
-
Bài tập 3: Một tia sáng truyền từ môi trường có chiết suất \( n_1 = 1.2 \) vào một môi trường có chiết suất \( n_2 = 2.0 \). Nếu góc khúc xạ là \( r = 20^\circ \), hãy tính góc tới \( i \).
Lời giải:
Áp dụng định luật Snell-Descartes:
\[
\frac{\sin(i)}{\sin(r)} = \frac{n_2}{n_1}
\]
\[
\sin(i) = \sin(20^\circ) \times \frac{2.0}{1.2} = 0.342 \times 1.667 \approx 0.57
\]Vậy \( i = \sin^{-1}(0.57) \approx 35^\circ \).
Những bài tập này giúp bạn hiểu rõ hơn về cách áp dụng công thức tính góc khúc xạ trong các tình huống khác nhau. Qua việc thực hành, bạn sẽ nắm vững hơn kiến thức và tự tin giải quyết các bài toán khúc xạ ánh sáng trong các kỳ thi hoặc trong thực tế.

V. Kết luận
Khúc xạ ánh sáng là một hiện tượng tự nhiên quan trọng, đóng vai trò cơ bản trong nhiều lĩnh vực khoa học và công nghệ. Việc hiểu rõ định luật Snell-Descartes và công thức tính góc khúc xạ không chỉ giúp giải quyết các bài toán quang học mà còn cung cấp nền tảng cho nhiều ứng dụng thực tiễn trong đời sống và công nghiệp.
Qua các phần đã thảo luận, chúng ta thấy rằng chiết suất là một yếu tố quan trọng quyết định hướng đi của tia sáng khi truyền qua các môi trường khác nhau. Khả năng áp dụng các công thức tính toán liên quan đến góc khúc xạ và chiết suất không chỉ là một yêu cầu về kiến thức lý thuyết mà còn là kỹ năng cần thiết trong nhiều lĩnh vực như thiết kế thấu kính, phân tích quang phổ, và nhiều công nghệ quang học tiên tiến khác.
Tổng kết lại, hiểu biết sâu sắc về khúc xạ ánh sáng và các yếu tố liên quan sẽ giúp chúng ta không chỉ nắm vững kiến thức vật lý mà còn mở ra nhiều cơ hội nghiên cứu và phát triển các công nghệ mới, phục vụ cho đời sống và các ngành công nghiệp hiện đại.