Chủ đề bài tập khúc xạ ánh sáng lớp 9: Bài viết này cung cấp bộ sưu tập bài tập khúc xạ ánh sáng lớp 9 với hướng dẫn chi tiết và lời giải đầy đủ. Hãy cùng khám phá các dạng bài tập từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi sắp tới.
Mục lục
Bài tập Khúc xạ Ánh sáng Lớp 9
Khúc xạ ánh sáng là một hiện tượng vật lý quan trọng trong chương trình Vật lý lớp 9. Dưới đây là một số bài tập giúp học sinh hiểu rõ hơn về hiện tượng này và cách áp dụng các công thức liên quan.
I. Lý thuyết về Khúc xạ Ánh sáng
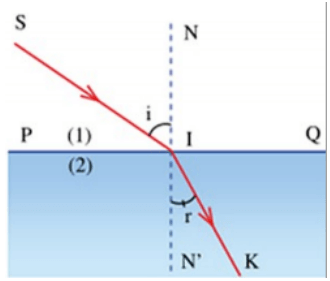
- Hiện tượng khúc xạ ánh sáng xảy ra khi tia sáng đi từ môi trường này sang môi trường khác, dẫn đến sự thay đổi về hướng đi của tia sáng.
- Công thức tính góc khúc xạ: \(\sin i \over \sin r = n\), trong đó \(i\) là góc tới, \(r\) là góc khúc xạ, \(n\) là chiết suất của môi trường.
- Chiết suất của môi trường là một đại lượng không có đơn vị, biểu diễn độ lớn của sự khúc xạ ánh sáng trong môi trường đó.
II. Bài tập Cơ bản
Dưới đây là một số bài tập cơ bản về khúc xạ ánh sáng để học sinh luyện tập:
- Cho một tia sáng truyền từ không khí vào nước với góc tới \(i = 30^\circ\). Chiết suất của nước là \(n = 1.33\). Tính góc khúc xạ \(r\).
- Một tia sáng đi từ thủy tinh (chiết suất \(n = 1.5\)) ra không khí với góc tới \(i = 45^\circ\). Tính góc khúc xạ \(r\) trong không khí.
- Một tia sáng chiếu tới mặt phân cách giữa hai môi trường với góc tới \(i = 60^\circ\) và góc khúc xạ \(r = 40^\circ\). Tính chiết suất của môi trường thứ hai so với môi trường thứ nhất.
III. Bài tập Nâng cao
Các bài tập nâng cao sẽ yêu cầu học sinh áp dụng linh hoạt kiến thức và công thức để giải quyết các tình huống phức tạp hơn:
- Cho một tia sáng đi từ không khí vào một lăng kính có chiết suất \(n = 1.6\). Góc tới là \(45^\circ\). Tính góc khúc xạ khi tia sáng ra khỏi lăng kính.
- Một tia sáng truyền từ nước vào thủy tinh với chiết suất của nước là \(n_1 = 1.33\) và của thủy tinh là \(n_2 = 1.5\). Tính góc khúc xạ nếu góc tới là \(30^\circ\).
- Tìm góc giới hạn phản xạ toàn phần khi tia sáng truyền từ một môi trường có chiết suất \(n_1 = 1.6\) vào môi trường có chiết suất \(n_2 = 1.33\).
IV. Đáp án Gợi ý
| Bài tập | Đáp án |
| Bài tập 1 | \(r \approx 22^\circ\) |
| Bài tập 2 | \(r \approx 28.1^\circ\) |
| Bài tập 3 | \(n = 1.5\) |
| Bài tập 4 | \(r \approx 26.3^\circ\) |
| Bài tập 5 | \(r \approx 26.7^\circ\) |
| Bài tập 6 | \(i_g \approx 56.4^\circ\) |
Những bài tập trên giúp học sinh nắm vững kiến thức về hiện tượng khúc xạ ánh sáng, đồng thời rèn luyện kỹ năng giải bài tập vật lý.
.png)
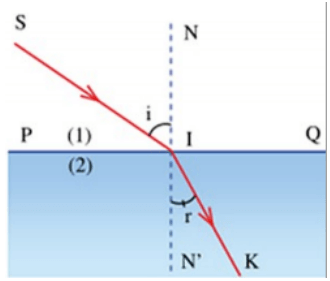
I. Giới thiệu về Khúc xạ Ánh sáng
Khúc xạ ánh sáng là một hiện tượng vật lý xảy ra khi tia sáng truyền qua ranh giới giữa hai môi trường trong suốt có chiết suất khác nhau, dẫn đến sự thay đổi về hướng đi của tia sáng. Hiện tượng này có vai trò quan trọng trong nhiều ứng dụng thực tế, từ thiết kế thấu kính quang học đến hiểu biết về các hiện tượng thiên nhiên như cầu vồng.
- Khái niệm khúc xạ ánh sáng: Khi ánh sáng truyền từ môi trường này sang môi trường khác với tốc độ khác nhau, hướng của tia sáng sẽ thay đổi, đây chính là hiện tượng khúc xạ.
- Chiết suất: Chiết suất của một môi trường là đại lượng đặc trưng cho khả năng làm chậm tốc độ ánh sáng trong môi trường đó, ký hiệu là \(n\). Công thức tính chiết suất là \(n = \frac{c}{v}\), trong đó \(c\) là tốc độ ánh sáng trong chân không và \(v\) là tốc độ ánh sáng trong môi trường đó.
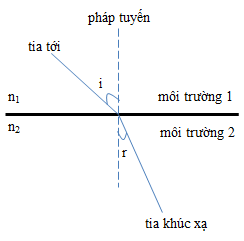
- Định luật khúc xạ ánh sáng: Định luật Snell mô tả mối quan hệ giữa góc tới (\(i\)) và góc khúc xạ (\(r\)) thông qua chiết suất của hai môi trường. Công thức định luật Snell: \(\frac{\sin i}{\sin r} = \frac{n_2}{n_1}\), trong đó \(n_1\) và \(n_2\) lần lượt là chiết suất của môi trường thứ nhất và môi trường thứ hai.
Hiện tượng khúc xạ ánh sáng không chỉ giúp chúng ta hiểu rõ hơn về thế giới tự nhiên mà còn được ứng dụng rộng rãi trong công nghệ, đặc biệt là trong lĩnh vực quang học như sản xuất kính mắt, thiết kế máy ảnh, và các thiết bị y tế.
II. Bài Tập Cơ Bản về Khúc Xạ Ánh Sáng
Dưới đây là một số bài tập cơ bản về khúc xạ ánh sáng, giúp học sinh hiểu rõ hơn về hiện tượng này và cách áp dụng các công thức liên quan. Các bài tập được thiết kế từ đơn giản đến phức tạp, phù hợp với chương trình Vật lý lớp 9.
-
Bài tập 1: Cho một tia sáng đi từ không khí vào nước với góc tới \(i = 30^\circ\). Biết chiết suất của nước là \(n = 1.33\). Hãy tính góc khúc xạ \(r\).
- Bước 1: Sử dụng định luật khúc xạ Snell: \(\frac{\sin i}{\sin r} = \frac{n_2}{n_1}\).
- Bước 2: Với \(n_1 = 1\) (chiết suất của không khí) và \(n_2 = 1.33\) (chiết suất của nước), tính \(\sin r = \frac{\sin i}{n_2} = \frac{\sin 30^\circ}{1.33}\).
- Bước 3: Tính giá trị của \(r\) bằng cách lấy \(\sin^{-1}\) (inversing function) của kết quả vừa tìm được.
-
Bài tập 2: Một tia sáng đi từ thủy tinh (chiết suất \(n = 1.5\)) ra không khí với góc tới \(i = 45^\circ\). Tính góc khúc xạ \(r\) trong không khí.
- Bước 1: Sử dụng công thức \(\frac{\sin i}{\sin r} = \frac{n_2}{n_1}\) với \(n_1 = 1.5\) và \(n_2 = 1\).
- Bước 2: Tính \(\sin r = \frac{1 \times \sin 45^\circ}{1.5}\).
- Bước 3: Tính góc khúc xạ \(r\) bằng cách sử dụng hàm \(\sin^{-1}\).
-
Bài tập 3: Tìm chiết suất của môi trường thứ hai nếu góc tới là \(60^\circ\) và góc khúc xạ là \(40^\circ\).
- Bước 1: Sử dụng công thức định luật Snell: \(\frac{\sin i}{\sin r} = \frac{n_2}{n_1}\).
- Bước 2: Tính \(n_2 = n_1 \times \frac{\sin i}{\sin r}\), trong đó \(n_1 = 1\) (chiết suất của không khí).
- Bước 3: Tính giá trị cụ thể của \(n_2\).
Những bài tập trên giúp củng cố kiến thức về khúc xạ ánh sáng và cách áp dụng định luật Snell trong các tình huống khác nhau. Học sinh nên luyện tập thường xuyên để nắm vững kỹ năng giải bài tập.

III. Bài Tập Nâng Cao và Ứng Dụng
Các bài tập nâng cao về khúc xạ ánh sáng không chỉ giúp học sinh hiểu sâu hơn về hiện tượng này mà còn cung cấp các ứng dụng thực tế, giúp kết nối kiến thức lý thuyết với các hiện tượng tự nhiên và công nghệ hiện đại. Dưới đây là một số bài tập nâng cao để bạn thử sức.
-
Bài tập 1: Tính góc khúc xạ trong lăng kính thủy tinh
- Đề bài: Một tia sáng chiếu vào lăng kính thủy tinh có chiết suất \(n = 1.6\) với góc tới \(i = 40^\circ\). Tính góc khúc xạ \(r\) khi tia sáng ra khỏi mặt bên kia của lăng kính.
- Bước 1: Xác định góc khúc xạ đầu tiên bằng định luật Snell: \(\frac{\sin i}{\sin r_1} = \frac{n}{1}\).
- Bước 2: Tính góc khúc xạ thứ hai dựa trên góc tới ở mặt phân cách thứ hai của lăng kính, sử dụng lại định luật Snell.
- Bước 3: Kết luận về góc lệch của tia sáng sau khi đi qua lăng kính.
-
Bài tập 2: Tính góc giới hạn của hiện tượng phản xạ toàn phần
- Đề bài: Một tia sáng truyền từ nước (chiết suất \(n = 1.33\)) vào không khí. Tính góc tới nhỏ nhất để xảy ra hiện tượng phản xạ toàn phần.
- Bước 1: Sử dụng công thức \(\sin i_g = \frac{n_2}{n_1}\) để tìm góc giới hạn \(i_g\), trong đó \(n_1 = 1.33\) và \(n_2 = 1\).
- Bước 2: Tính giá trị cụ thể của góc giới hạn bằng cách lấy \(\sin^{-1}\) của kết quả vừa tìm được.
- Bước 3: Kết luận về điều kiện để xảy ra hiện tượng phản xạ toàn phần.
-
Bài tập 3: Ứng dụng của khúc xạ ánh sáng trong thiết kế thấu kính
- Đề bài: Một thấu kính hội tụ được làm từ chất liệu có chiết suất \(n = 1.5\). Tính tiêu cự của thấu kính khi các tia sáng song song với trục chính chiếu vào và hội tụ tại một điểm trên trục.
- Bước 1: Sử dụng công thức thấu kính mỏng: \(\frac{1}{f} = (n - 1) \left(\frac{1}{R_1} - \frac{1}{R_2}\right)\), trong đó \(R_1\) và \(R_2\) là bán kính cong của hai mặt thấu kính.
- Bước 2: Tính tiêu cự \(f\) dựa trên các thông số của thấu kính.
- Bước 3: Kết luận về khả năng hội tụ của thấu kính dựa trên tiêu cự vừa tính.
Các bài tập nâng cao này không chỉ giúp bạn nắm vững kiến thức về khúc xạ ánh sáng mà còn mở rộng khả năng áp dụng vào các lĩnh vực như quang học, vật lý và các ứng dụng thực tiễn trong đời sống. Việc hiểu rõ bản chất và cách áp dụng các hiện tượng quang học sẽ giúp bạn đạt kết quả cao trong học tập và nghiên cứu.

IV. Phân tích và Giải thích chi tiết từng bài tập
Để giúp học sinh nắm vững hơn về hiện tượng khúc xạ ánh sáng, dưới đây là phân tích và giải thích chi tiết từng bài tập, kèm theo các bước giải cụ thể.
-
Bài tập 1: Tính góc khúc xạ \(r\) khi tia sáng đi từ không khí vào nước với góc tới \(i = 30^\circ\).
- Bước 1: Sử dụng định luật Snell: \(\frac{\sin i}{\sin r} = \frac{n_2}{n_1}\). Ở đây, \(n_1 = 1\) (chiết suất không khí) và \(n_2 = 1.33\) (chiết suất nước).
- Bước 2: Tính \(\sin r = \frac{\sin 30^\circ}{1.33}\).
- Bước 3: Giải để tìm \(r\): \(r = \sin^{-1}\left(\frac{\sin 30^\circ}{1.33}\right)\).
- Giải thích: Kết quả cho thấy góc khúc xạ \(r\) nhỏ hơn góc tới \(i\), điều này phù hợp với hiện tượng khúc xạ khi tia sáng đi từ môi trường chiết suất thấp sang chiết suất cao.
-
Bài tập 2: Tính góc khúc xạ khi tia sáng đi từ thủy tinh (chiết suất \(n = 1.5\)) ra không khí với góc tới \(i = 45^\circ\).
- Bước 1: Sử dụng định luật Snell: \(\frac{\sin i}{\sin r} = \frac{n_2}{n_1}\), với \(n_1 = 1.5\) và \(n_2 = 1\).
- Bước 2: Tính \(\sin r = \frac{\sin 45^\circ}{1.5}\).
- Bước 3: Tìm \(r\) bằng cách lấy hàm nghịch đảo của \(\sin\): \(r = \sin^{-1}\left(\frac{\sin 45^\circ}{1.5}\right)\).
- Giải thích: Vì chiết suất của thủy tinh lớn hơn không khí, nên khi ánh sáng truyền từ thủy tinh ra không khí, góc khúc xạ lớn hơn góc tới.
-
Bài tập 3: Tìm chiết suất của môi trường nếu góc tới là \(60^\circ\) và góc khúc xạ là \(40^\circ\).
- Bước 1: Sử dụng định luật Snell: \(\frac{\sin i}{\sin r} = \frac{n_2}{n_1}\), với \(i = 60^\circ\) và \(r = 40^\circ\).
- Bước 2: Tính \(n_2 = n_1 \times \frac{\sin i}{\sin r}\), trong đó \(n_1 = 1\) (chiết suất không khí).
- Bước 3: Kết quả là \(n_2 = 1 \times \frac{\sin 60^\circ}{\sin 40^\circ}\), tính toán ra chiết suất của môi trường thứ hai.
- Giải thích: Bài tập này giúp xác định môi trường mới dựa trên sự thay đổi hướng đi của ánh sáng, minh họa cách ánh sáng bị bẻ cong khi đi qua các môi trường khác nhau.
Việc phân tích chi tiết từng bài tập giúp học sinh hiểu rõ hơn về cách áp dụng các công thức và định luật trong vật lý, đồng thời nâng cao khả năng tư duy và giải quyết vấn đề một cách logic.

V. Đề thi và Đáp án tham khảo
Dưới đây là một đề thi tham khảo về khúc xạ ánh sáng dành cho học sinh lớp 9, kèm theo đáp án chi tiết. Đề thi này giúp các em rèn luyện kỹ năng và củng cố kiến thức đã học.
1. Đề thi tham khảo
-
Câu 1: Một tia sáng chiếu từ không khí vào nước với góc tới \(i = 35^\circ\). Tính góc khúc xạ \(r\) khi tia sáng truyền vào nước. Chiết suất của nước so với không khí là \(n = 1.33\).
-
Câu 2: Giải thích hiện tượng phản xạ toàn phần và tính góc giới hạn khi tia sáng truyền từ thủy tinh (chiết suất \(n = 1.5\)) vào không khí.
-
Câu 3: Tính tiêu cự của một thấu kính hội tụ làm từ chất liệu có chiết suất \(n = 1.6\), nếu bán kính cong của các mặt cầu lần lượt là \(R_1 = 10 cm\) và \(R_2 = -15 cm\).
2. Đáp án chi tiết
-
Câu 1:
- Bước 1: Áp dụng định luật khúc xạ Snell: \(\frac{\sin i}{\sin r} = \frac{n_2}{n_1}\), với \(n_1 = 1\) (chiết suất không khí) và \(n_2 = 1.33\) (chiết suất nước).
- Bước 2: Tính \(\sin r = \frac{\sin 35^\circ}{1.33}\).
- Bước 3: Tìm giá trị của \(r\) bằng cách lấy hàm nghịch đảo của \(\sin\): \(r = \sin^{-1}\left(\frac{\sin 35^\circ}{1.33}\right)\).
- Kết quả: Góc khúc xạ \(r\) được tính ra là khoảng \(25.7^\circ\).
-
Câu 2:
- Bước 1: Hiện tượng phản xạ toàn phần xảy ra khi tia sáng đi từ môi trường có chiết suất lớn sang môi trường có chiết suất nhỏ và góc tới lớn hơn góc giới hạn.
- Bước 2: Sử dụng công thức tính góc giới hạn \(i_g\): \(\sin i_g = \frac{n_2}{n_1}\), với \(n_1 = 1.5\) và \(n_2 = 1\).
- Bước 3: Tính \(i_g = \sin^{-1}\left(\frac{1}{1.5}\right)\).
- Kết quả: Góc giới hạn \(i_g\) xấp xỉ \(41.8^\circ\). Tia sáng sẽ phản xạ toàn phần nếu góc tới lớn hơn giá trị này.
-
Câu 3:
- Bước 1: Sử dụng công thức của thấu kính mỏng: \(\frac{1}{f} = (n - 1)\left(\frac{1}{R_1} - \frac{1}{R_2}\right)\).
- Bước 2: Thay các giá trị vào công thức: \(f = \frac{1}{(1.6 - 1)\left(\frac{1}{10} - \frac{1}{-15}\right)}\).
- Bước 3: Tính toán để tìm tiêu cự \(f\).
- Kết quả: Tiêu cự của thấu kính là khoảng \(24 cm\).
Đề thi và đáp án này không chỉ giúp các em ôn luyện kiến thức mà còn cung cấp các bước giải cụ thể để các em có thể hiểu rõ và áp dụng tốt trong các kỳ thi.