Góc Khúc Xạ Là Gì? Khám Phá Hiện Tượng Quang Học Kỳ Diệu

Trong vật lý, đặc biệt là trong quang học, "góc khúc xạ" là một khái niệm quan trọng được sử dụng để mô tả sự thay đổi hướng của một tia sáng khi nó truyền từ một môi trường này sang một môi trường khác có chiết suất khác nhau.

Định Nghĩa Góc Khúc Xạ

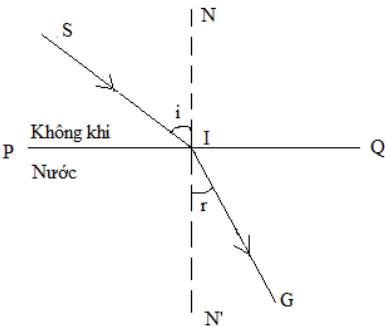
Góc khúc xạ là góc được tạo bởi tia khúc xạ và pháp tuyến tại điểm mà tia sáng gặp mặt phân cách giữa hai môi trường. Ký hiệu của góc khúc xạ thường là \( r \).

Định Luật Khúc Xạ Ánh Sáng

Định luật khúc xạ ánh sáng, còn được biết đến là định luật Snell, mô tả mối quan hệ giữa góc tới \( i \) và góc khúc xạ \( r \). Công thức của định luật Snell được viết như sau:

\[
n_1 \sin i = n_2 \sin r
\]

Trong đó:

• \( n_1 \) là chiết suất của môi trường đầu tiên.
• \( n_2 \) là chiết suất của môi trường thứ hai.
• \( i \) là góc tới, góc tạo bởi tia tới và pháp tuyến.
• \( r \) là góc khúc xạ, góc tạo bởi tia khúc xạ và pháp tuyến.

Ứng Dụng Của Góc Khúc Xạ

Hiểu rõ về góc khúc xạ và định luật Snell giúp giải thích nhiều hiện tượng quang học trong cuộc sống, chẳng hạn như:

• Sự gãy khúc của ánh sáng khi đi qua lăng kính.
• Sự hình thành của cầu vồng khi ánh sáng mặt trời khúc xạ qua các giọt nước trong không khí.
• Hiện tượng ảo ảnh khi ánh sáng bị khúc xạ trong các lớp không khí có mật độ khác nhau.

Công Thức Tính Góc Khúc Xạ

Để tính toán góc khúc xạ, chúng ta có thể sử dụng công thức:

\[
\sin r = \frac{n_1}{n_2} \sin i
\]

Từ công thức này, nếu biết giá trị của chiết suất hai môi trường và góc tới, ta có thể xác định được góc khúc xạ \( r \).

Kết Luận

Góc khúc xạ là một khái niệm cơ bản nhưng cực kỳ quan trọng trong quang học và các ứng dụng liên quan đến ánh sáng. Việc nắm vững kiến thức về góc khúc xạ không chỉ giúp chúng ta hiểu rõ hơn về các hiện tượng quang học mà còn ứng dụng trong nhiều lĩnh vực khoa học và công nghệ.

Góc khúc xạ là một khái niệm trong quang học, mô tả góc mà tại đó tia sáng bị bẻ cong khi nó truyền từ một môi trường này sang một môi trường khác có chiết suất khác nhau. Góc khúc xạ được đo giữa tia khúc xạ và pháp tuyến tại điểm mà tia sáng tiếp xúc với mặt phân cách giữa hai môi trường.

Chiết suất của mỗi môi trường ảnh hưởng trực tiếp đến góc khúc xạ. Khi ánh sáng di chuyển từ một môi trường có chiết suất thấp sang một môi trường có chiết suất cao, tia sáng bị bẻ cong về phía pháp tuyến, và ngược lại, khi di chuyển từ môi trường có chiết suất cao sang môi trường có chiết suất thấp, tia sáng bị bẻ cong ra xa pháp tuyến.

Theo định luật Snell, mối quan hệ giữa góc tới \( i \) và góc khúc xạ \( r \) được xác định bởi phương trình:

\[
n_1 \sin i = n_2 \sin r
\]

Trong đó:

• \( n_1 \): Chiết suất của môi trường mà ánh sáng đi tới.
• \( n_2 \): Chiết suất của môi trường mà ánh sáng truyền vào.
• \( i \): Góc tới, là góc giữa tia sáng tới và pháp tuyến.
• \( r \): Góc khúc xạ, là góc giữa tia khúc xạ và pháp tuyến.

Góc khúc xạ giúp giải thích nhiều hiện tượng quang học trong tự nhiên và kỹ thuật, từ sự bẻ cong của ánh sáng qua lăng kính đến sự tạo ra các ảo ảnh thị giác. Việc hiểu rõ định nghĩa và cách tính góc khúc xạ là bước đầu tiên để nắm vững các nguyên lý quang học cơ bản.

Định luật khúc xạ ánh sáng mô tả cách mà tia sáng thay đổi hướng khi đi từ môi trường này sang môi trường khác. Hiện tượng này xảy ra khi có sự khác biệt về mật độ quang học giữa hai môi trường, dẫn đến sự thay đổi về tốc độ truyền ánh sáng.

2.1 Công Thức Định Luật Snell

Định luật khúc xạ, thường được gọi là Định luật Snell, phát biểu rằng:

\[
n_1 \sin(i) = n_2 \sin(r)
\]

Trong đó:

• \( n_1 \) và \( n_2 \) là chiết suất của môi trường 1 và 2.
• \( i \) là góc tới, là góc giữa tia tới và pháp tuyến tại điểm tới.
• \( r \) là góc khúc xạ, là góc giữa tia khúc xạ và pháp tuyến tại điểm tới.

Công thức trên chỉ ra rằng tỉ số giữa sin của góc tới và sin của góc khúc xạ tỉ lệ với chiết suất của các môi trường tương ứng. Điều này cho phép chúng ta tính toán góc khúc xạ khi biết chiết suất của hai môi trường và góc tới.

2.2 Giải Thích Mối Quan Hệ Giữa Góc Tới Và Góc Khúc Xạ

Góc tới và góc khúc xạ có mối quan hệ mật thiết với nhau qua công thức của Định luật Snell. Tùy thuộc vào chiết suất của hai môi trường, góc khúc xạ có thể lớn hơn hoặc nhỏ hơn góc tới:

• Nếu \( n_2 > n_1 \) (môi trường 2 chiết quang hơn môi trường 1), góc khúc xạ \( r \) sẽ nhỏ hơn góc tới \( i \).
• Nếu \( n_2 < n_1 \) (môi trường 2 chiết quang kém hơn môi trường 1), góc khúc xạ \( r \) sẽ lớn hơn góc tới \( i \).

Ví dụ, khi tia sáng truyền từ không khí (có chiết suất khoảng 1) vào nước (có chiết suất khoảng 1,33), góc khúc xạ sẽ nhỏ hơn góc tới. Ngược lại, nếu tia sáng truyền từ nước ra không khí, góc khúc xạ sẽ lớn hơn góc tới.

Định luật này là nền tảng quan trọng trong quang học, giúp giải thích nhiều hiện tượng trong tự nhiên như sự khúc xạ qua lăng kính, hiện tượng cầu vồng, và sự thay đổi vị trí của các ngôi sao khi chúng ta quan sát từ Trái Đất.

Góc khúc xạ của một tia sáng khi đi qua mặt phân cách giữa hai môi trường chịu ảnh hưởng bởi nhiều yếu tố khác nhau. Dưới đây là các yếu tố chính:

3.1 Chiết Suất Của Môi Trường

Chiết suất của môi trường là một yếu tố quan trọng quyết định góc khúc xạ. Chiết suất xác định mức độ mà môi trường làm giảm tốc độ ánh sáng. Công thức khúc xạ ánh sáng có dạng:

\[
n_1 \sin(i) = n_2 \sin(r)
\]

Nếu chiết suất của môi trường mà tia sáng truyền vào (n₂) lớn hơn chiết suất của môi trường xuất phát (n₁), thì góc khúc xạ sẽ nhỏ hơn góc tới và ngược lại.

3.2 Góc Tới Của Tia Sáng

Góc tới là góc giữa tia sáng và pháp tuyến tại điểm tới trên mặt phân cách. Khi góc tới tăng, góc khúc xạ cũng thay đổi theo. Tuy nhiên, mối quan hệ giữa góc tới và góc khúc xạ không phải là tuyến tính, mà phụ thuộc vào chiết suất của các môi trường theo công thức Snell.

\[
\frac{\sin(i)}{\sin(r)} = \frac{n_2}{n_1}
\]

3.3 Bản Chất Của Vật Liệu

Bản chất vật liệu của môi trường (như độ trong suốt, cấu trúc phân tử) cũng ảnh hưởng đến chiết suất và do đó ảnh hưởng đến góc khúc xạ. Các vật liệu khác nhau có chiết suất khác nhau, ví dụ, chiết suất của thủy tinh khác với chiết suất của nước hay không khí, dẫn đến sự thay đổi góc khúc xạ khi tia sáng truyền qua các chất liệu này.

Những yếu tố này kết hợp lại xác định góc khúc xạ của tia sáng khi nó di chuyển giữa các môi trường khác nhau. Hiểu rõ những yếu tố này giúp chúng ta ứng dụng hiện tượng khúc xạ trong các thiết bị quang học như lăng kính, kính hiển vi và thấu kính.

Hiện tượng khúc xạ ánh sáng không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng quan trọng trong thực tế. Dưới đây là một số ví dụ tiêu biểu về ứng dụng của góc khúc xạ:

4.1 Sự Khúc Xạ Qua Lăng Kính

Khi ánh sáng truyền qua một lăng kính, nó bị khúc xạ hai lần: lần đầu tiên khi ánh sáng đi vào lăng kính và lần thứ hai khi nó thoát ra. Mỗi lần khúc xạ, góc của tia sáng thay đổi, tạo ra hiện tượng tách ánh sáng trắng thành các màu sắc khác nhau, như một cầu vồng nhỏ. Điều này được sử dụng rộng rãi trong các dụng cụ quang học như kính hiển vi và kính thiên văn.

4.2 Hiện Tượng Cầu Vồng

Cầu vồng là một ví dụ điển hình của sự khúc xạ và phản xạ ánh sáng. Ánh sáng mặt trời bị khúc xạ khi đi vào các hạt nước trong không khí, sau đó bị phản xạ bên trong hạt nước và cuối cùng lại bị khúc xạ một lần nữa khi ra khỏi hạt nước. Quá trình này tạo ra một quang phổ của các màu sắc mà chúng ta thấy trong cầu vồng.

4.3 Ảo Ảnh Trong Tự Nhiên

Ảo ảnh là một hiện tượng quang học mà trong đó ánh sáng bị khúc xạ khi truyền qua các lớp không khí có mật độ khác nhau. Điều này thường xảy ra trên các bề mặt nóng, chẳng hạn như mặt đường vào ngày nắng nóng, nơi bạn có thể thấy hình ảnh của nước trên đường dù thực tế không có nước. Ảo ảnh là kết quả của sự thay đổi liên tục của chỉ số khúc xạ của không khí theo nhiệt độ.

Các ứng dụng của hiện tượng khúc xạ ánh sáng không chỉ giúp chúng ta hiểu rõ hơn về tự nhiên mà còn mở ra nhiều công nghệ tiên tiến, từ các thiết bị quang học cho đến việc dự đoán và giải thích các hiện tượng thiên nhiên.

Để tính toán góc khúc xạ, ta có thể sử dụng định luật Snell, công thức này mô tả mối quan hệ giữa góc tới và góc khúc xạ khi ánh sáng di chuyển qua mặt phân cách giữa hai môi trường có chiết suất khác nhau.

1. 5.1 Sử Dụng Công Thức Định Luật Snell

   Định luật Snell được thể hiện bằng công thức sau:

   
   \[
   n_1 \sin(i) = n_2 \sin(r)
   \]

   Trong đó:

   • \(n_1\) và \(n_2\) là chiết suất của hai môi trường, với \(n_1\) là chiết suất của môi trường chứa tia tới, và \(n_2\) là chiết suất của môi trường chứa tia khúc xạ.
   • \(i\) là góc tới, và \(r\) là góc khúc xạ.

2. 5.2 Ví Dụ Tính Toán Cụ Thể

   Giả sử tia sáng đi từ không khí (có chiết suất \(n_1 \approx 1\)) vào nước (có chiết suất \(n_2 = 1.33\)). Nếu góc tới \(i = 30^\circ\), ta có thể tính góc khúc xạ \(r\) như sau:

   
   \[
   \sin(r) = \frac{n_1}{n_2} \sin(i) = \frac{1}{1.33} \sin(30^\circ) \approx 0.375
   \]

   Suy ra:

   
   \[
   r = \arcsin(0.375) \approx 22^\circ
   \]

   Vậy góc khúc xạ \(r\) khi ánh sáng đi từ không khí vào nước với góc tới \(i = 30^\circ\) là khoảng \(22^\circ\).

Khi nghiên cứu về góc khúc xạ, có một số yếu tố và hiện tượng cần lưu ý để đảm bảo tính chính xác và hiệu quả trong các thí nghiệm và ứng dụng thực tế.

6.1 Sự Sai Số Trong Thí Nghiệm

Sai số là yếu tố không thể tránh khỏi trong bất kỳ thí nghiệm nào liên quan đến góc khúc xạ. Sai số có thể phát sinh từ các yếu tố như độ chính xác của dụng cụ đo, môi trường thí nghiệm không ổn định, hoặc sự không đồng đều của các bề mặt phản xạ và khúc xạ.

• Sai số hệ thống: Là sai số do các thiết bị đo lường không hoàn toàn chính xác hoặc do phương pháp đo không chuẩn xác. Loại sai số này có thể được giảm thiểu bằng cách hiệu chuẩn thiết bị trước khi tiến hành thí nghiệm.
• Sai số ngẫu nhiên: Là sai số do các yếu tố ngẫu nhiên như rung động, thay đổi nhiệt độ, hoặc lỗi của người thí nghiệm. Để giảm thiểu loại sai số này, cần tiến hành thí nghiệm nhiều lần và lấy giá trị trung bình của các lần đo.

6.2 Ảnh Hưởng Của Nhiệt Độ Và Áp Suất

Nhiệt độ và áp suất là những yếu tố quan trọng ảnh hưởng đến chiết suất của môi trường, từ đó tác động trực tiếp đến góc khúc xạ.

• Nhiệt độ: Khi nhiệt độ tăng, chiết suất của môi trường thường giảm, dẫn đến sự thay đổi của góc khúc xạ. Trong các thí nghiệm liên quan đến khúc xạ, cần kiểm soát nhiệt độ để đảm bảo kết quả chính xác.
• Áp suất: Áp suất cũng có ảnh hưởng tương tự như nhiệt độ. Đặc biệt trong các môi trường khí, khi áp suất thay đổi, mật độ khí cũng thay đổi, dẫn đến thay đổi trong chiết suất và góc khúc xạ.

Do đó, khi thực hiện các thí nghiệm hoặc nghiên cứu liên quan đến góc khúc xạ, cần đặc biệt chú ý đến các yếu tố nhiệt độ và áp suất, đồng thời áp dụng các biện pháp kiểm soát môi trường một cách hợp lý.

Để hiểu sâu hơn về hiện tượng khúc xạ ánh sáng và góc khúc xạ, bạn có thể tham khảo các tài liệu sau:

• Sách giáo khoa Vật Lý: Các sách giáo khoa vật lý ở cấp trung học phổ thông, đặc biệt là lớp 11, cung cấp nền tảng lý thuyết vững chắc về hiện tượng khúc xạ ánh sáng, định luật Snell, và các yếu tố ảnh hưởng đến góc khúc xạ.
• Các nghiên cứu khoa học: Nhiều bài báo và tài liệu khoa học đã phân tích chi tiết về hiện tượng khúc xạ và ứng dụng trong thực tế. Bạn có thể tìm các tài liệu này qua các trang web học thuật hoặc các cơ sở dữ liệu khoa học.
• Trang web giáo dục: Nhiều trang web như Hoc24.vn hay Manta.edu.vn cung cấp các bài giảng, bài tập và ví dụ cụ thể về khúc xạ ánh sáng. Các ví dụ tính toán cụ thể trên các trang này có thể giúp bạn củng cố kiến thức và ứng dụng thực tế.
• Video hướng dẫn: Các video học tập trên YouTube hoặc các nền tảng giáo dục khác cũng là một nguồn tài liệu hữu ích. Những video này thường bao gồm các mô phỏng và minh họa trực quan giúp bạn dễ dàng nắm bắt các khái niệm phức tạp.

Việc tham khảo đa dạng các nguồn tài liệu sẽ giúp bạn có cái nhìn toàn diện và sâu sắc hơn về hiện tượng khúc xạ ánh sáng, từ lý thuyết cơ bản đến các ứng dụng thực tiễn và nghiên cứu nâng cao.