Chủ đề công thức tính cảm ứng từ: Công thức tính cảm ứng từ là một khái niệm quan trọng trong vật lý và kỹ thuật điện. Bài viết này cung cấp hướng dẫn chi tiết về cách tính toán cảm ứng từ trong các trường hợp khác nhau, đồng thời giới thiệu các ứng dụng thực tế của công thức này trong cuộc sống hàng ngày và các ngành công nghiệp hiện đại.
Mục lục
Công Thức Tính Cảm Ứng Từ
Cảm ứng từ là một khía cạnh quan trọng của vật lý điện từ học, liên quan đến từ trường do dòng điện tạo ra. Đây là một khái niệm cơ bản trong vật lý và được sử dụng rộng rãi trong các lĩnh vực như điện tử, công nghệ, và các thiết bị đo lường. Dưới đây là tổng hợp chi tiết về các công thức tính cảm ứng từ.
1. Công Thức Biô-Savart
Công thức Biô-Savart cho phép tính toán từ trường \( \mathbf{B} \) tại bất kỳ điểm nào do dòng điện tạo ra:
\[
\mathbf{B}(\mathbf{r}) = \frac{\mu_0}{4\pi} \int_C \frac{I \cdot d\mathbf{l} \times \mathbf{r'}}{|\mathbf{r'}|^3}
\]
- \(\mu_0\): hằng số từ trường (4π x 10-7 T.m/A)
- \(I\): cường độ dòng điện qua dây dẫn
- \(d\mathbf{l}\): phần tử dài vô cùng nhỏ của dây dẫn
- \(\mathbf{r'}\): vectơ vị trí từ phần tử dòng điện đến điểm mà tại đó từ trường được xác định
2. Dòng Điện Trong Dây Dẫn Thẳng Dài Vô Hạn
Cảm ứng từ tại một điểm cách dây dẫn một khoảng \(r\) được tính theo công thức:
\[
B = \frac{\mu_0 I}{2\pi r}
\]
- \(B\): cảm ứng từ
- \(r\): khoảng cách từ dây đến điểm xét
3. Dòng Điện Trong Vòng Dây Dẫn Tròn
Cảm ứng từ tại tâm của vòng dây được tính theo công thức:
\[
B = \frac{\mu_0 I}{2R}
\]
- \(R\): bán kính của vòng dây
4. Dòng Điện Trong Ống Dây (Solenoid)
Cảm ứng từ bên trong một solenoid dài được tính theo công thức:
\[
B = \mu_0 n I
\]
- \(n\): số vòng dây trên một đơn vị chiều dài
- \(I\): cường độ dòng điện qua mỗi vòng
5. Các Yếu Tố Ảnh Hưởng Đến Cảm Ứng Từ
Các yếu tố chính ảnh hưởng đến độ lớn của cảm ứng từ bao gồm:
- Cường độ dòng điện: Độ lớn của cảm ứng từ tỷ lệ thuận với cường độ của dòng điện chạy qua dây dẫn.
- Khoảng cách: Cảm ứng từ giảm theo sự tăng khoảng cách từ nguồn tạo ra từ trường đến điểm đang xét.
- Đường kính của vòng dây: Đường kính của vòng dây ảnh hưởng trực tiếp đến độ lớn cảm ứng từ tại tâm vòng dây.
- Tính chất của môi trường xung quanh: Môi trường xung quanh có thể làm thay đổi độ lớn của cảm ứng từ, đặc biệt khi có sự hiện diện của các vật liệu từ tính.
6. Đơn Vị Đo Cảm Ứng Từ
Đơn vị đo cảm ứng từ là Tesla (T). Ngoài Tesla, trong một số ngữ cảnh khác, các đơn vị khác như Gauss (Gs) hoặc γ (y) cũng được sử dụng.
7. Ứng Dụng Thực Tế
Cảm ứng từ có ứng dụng rộng rãi trong cuộc sống hàng ngày, chẳng hạn như:
- Trong các động cơ điện và máy phát điện.
- Trong các cảm biến từ để đo độ dày của các tạp chất bám vào thành ống sắt.
- Trong các thiết bị điều khiển từ xa như cửa tự động, chuông cửa không dây, và hệ thống báo trộm.

.png)
1. Giới Thiệu Về Cảm Ứng Từ
Cảm ứng từ là một khái niệm quan trọng trong vật lý, đặc biệt là trong lĩnh vực điện từ học. Nó mô tả từ trường sinh ra xung quanh dòng điện hoặc vật liệu từ tính và được biểu diễn bằng vectơ từ trường \( \mathbf{B} \). Cảm ứng từ giúp xác định độ lớn và hướng của từ trường tại một điểm nhất định, đóng vai trò quan trọng trong nhiều ứng dụng kỹ thuật và công nghệ.
Trong thực tế, cảm ứng từ có thể được tạo ra bởi các nguồn khác nhau, bao gồm:
- Dòng điện: Dòng điện chạy qua dây dẫn tạo ra từ trường xung quanh nó.
- Nam châm vĩnh cửu: Các nam châm tạo ra từ trường ổn định mà không cần nguồn điện.
- Vật liệu từ tính: Các vật liệu như sắt hoặc niken khi đặt trong từ trường sẽ trở nên từ hóa và tạo ra cảm ứng từ.
Đơn vị đo của cảm ứng từ trong hệ SI là Tesla (T), trong đó 1 Tesla tương đương với một Newton trên mỗi Ampe mét. Ngoài ra, trong một số ngữ cảnh, đơn vị Gauss (Gs) cũng được sử dụng, với 1 Tesla = 10,000 Gauss.
Khái niệm cảm ứng từ có ý nghĩa quan trọng trong nhiều ứng dụng thực tiễn như:
- Trong các thiết bị điện tử: Cảm ứng từ được sử dụng trong các cuộn dây, máy phát điện, động cơ điện và các thiết bị cảm biến.
- Trong nghiên cứu khoa học: Từ trường và cảm ứng từ là nền tảng cho việc nghiên cứu về điện từ học, từ trường của Trái Đất và các hiện tượng liên quan.
- Trong y tế: Các máy quét MRI (Cộng hưởng từ) dựa trên nguyên lý cảm ứng từ để tạo ra hình ảnh chi tiết của các cơ quan nội tạng.
2. Công Thức Tính Cảm Ứng Từ
Công thức tính cảm ứng từ là một phần quan trọng trong lĩnh vực điện từ học, giúp chúng ta xác định được độ lớn của từ trường tại một điểm cụ thể trong không gian. Dưới đây là các công thức cơ bản và cách tính cảm ứng từ trong các trường hợp khác nhau:
2.1. Công Thức Biô-Savart
Công thức Biô-Savart được sử dụng để tính cảm ứng từ tại một điểm bất kỳ do dòng điện tạo ra. Công thức tổng quát là:
\[
\mathbf{B}(\mathbf{r}) = \frac{\mu_0}{4\pi} \int_C \frac{I \cdot d\mathbf{l} \times \mathbf{r'}}{|\mathbf{r'}|^3}
\]
- \(\mu_0\): Hằng số từ trường trong chân không (\(4\pi \times 10^{-7}\) T.m/A)
- \(I\): Cường độ dòng điện qua dây dẫn
- \(d\mathbf{l}\): Phần tử dài của dây dẫn
- \(\mathbf{r'}\): Vectơ từ vị trí phần tử dòng điện đến điểm cần tính
2.2. Dòng Điện Trong Dây Dẫn Thẳng Dài Vô Hạn
Đối với một dòng điện chạy trong dây dẫn thẳng dài vô hạn, cảm ứng từ tại một điểm cách dây một khoảng \(r\) được tính bằng công thức:
\[
B = \frac{\mu_0 I}{2\pi r}
\]
- \(B\): Cảm ứng từ tại điểm xét
- \(\mu_0\): Hằng số từ trường
- \(I\): Cường độ dòng điện
- \(r\): Khoảng cách từ dây dẫn đến điểm cần tính
2.3. Cảm Ứng Từ Trong Vòng Dây Dẫn Tròn
Cảm ứng từ tại tâm của một vòng dây dẫn tròn có bán kính \(R\) và dòng điện \(I\) được tính như sau:
\[
B = \frac{\mu_0 I}{2R}
\]
- \(R\): Bán kính của vòng dây
- \(I\): Cường độ dòng điện chạy qua vòng dây
2.4. Cảm Ứng Từ Trong Ống Dây (Solenoid)
Trong trường hợp của một ống dây (solenoid) dài, cảm ứng từ bên trong ống dây được tính bằng công thức:
\[
B = \mu_0 n I
\]
- \(n\): Số vòng dây trên mỗi đơn vị chiều dài của ống dây
- \(I\): Cường độ dòng điện chạy qua mỗi vòng dây
2.5. Công Thức Tính Cảm Ứng Từ Tổng Quát
Trong các trường hợp phức tạp hơn, cảm ứng từ có thể được tính bằng cách tích hợp hoặc sử dụng các mô hình số hóa tùy thuộc vào hình dạng của vật dẫn điện và cấu trúc từ trường.

3. Các Yếu Tố Ảnh Hưởng Đến Cảm Ứng Từ
Cảm ứng từ là một đại lượng quan trọng trong vật lý, chịu ảnh hưởng bởi nhiều yếu tố khác nhau. Việc hiểu rõ các yếu tố này giúp ta dự đoán và kiểm soát từ trường trong các ứng dụng thực tế. Dưới đây là những yếu tố chính ảnh hưởng đến cảm ứng từ:
3.1. Cường Độ Dòng Điện
Cảm ứng từ tỉ lệ thuận với cường độ dòng điện \(I\). Khi dòng điện tăng, cảm ứng từ tạo ra cũng tăng theo, thể hiện qua các công thức:
\[
B = \frac{\mu_0 I}{2\pi r} \quad \text{(dòng điện thẳng dài)}
\]
Do đó, việc điều chỉnh cường độ dòng điện là một cách hiệu quả để thay đổi cường độ của từ trường.
3.2. Khoảng Cách Từ Nguồn Tạo Từ Trường
Cảm ứng từ giảm dần khi khoảng cách từ nguồn tạo từ trường đến điểm xét tăng lên. Trong trường hợp của dây dẫn thẳng dài, công thức:
\[
B = \frac{\mu_0 I}{2\pi r}
\]
cho thấy cảm ứng từ giảm theo hàm số nghịch đảo của khoảng cách \(r\). Điều này có nghĩa là khi khoảng cách tăng, cảm ứng từ sẽ giảm đi.
3.3. Hình Dạng Và Kích Thước Dây Dẫn
Hình dạng và kích thước của dây dẫn ảnh hưởng lớn đến phân bố và cường độ của từ trường. Ví dụ, trong một vòng dây tròn, cảm ứng từ tại tâm vòng dây được tính bằng:
\[
B = \frac{\mu_0 I}{2R}
\]
Với \(R\) là bán kính của vòng dây, cho thấy cảm ứng từ phụ thuộc vào kích thước của vòng dây. Dây dẫn có hình dạng phức tạp hơn sẽ yêu cầu các công thức tính toán chi tiết hơn để xác định cảm ứng từ.
3.4. Môi Trường Xung Quanh
Vật liệu môi trường xung quanh cũng ảnh hưởng đến cảm ứng từ. Trong môi trường chân không, từ trường được mô tả bởi hằng số \(\mu_0\). Tuy nhiên, nếu môi trường chứa các vật liệu từ tính như sắt, thép, cảm ứng từ sẽ bị tăng cường đáng kể. Hằng số từ thẩm \(\mu\) của vật liệu có ảnh hưởng trực tiếp đến từ trường, với công thức tổng quát:
\[
B = \mu n I
\]
Vì vậy, chọn lựa và kiểm soát vật liệu trong môi trường là yếu tố quan trọng để điều chỉnh từ trường.
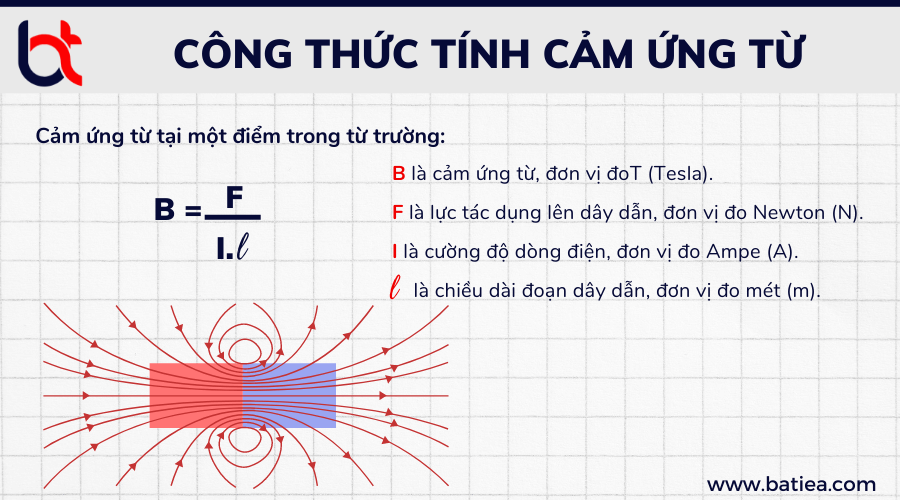
4. Đơn Vị Đo Lường Cảm Ứng Từ
Trong vật lý, cảm ứng từ được đo bằng đơn vị Tesla (ký hiệu: T) trong hệ đơn vị quốc tế SI. Đây là đơn vị chuẩn để xác định cường độ của từ trường. Một Tesla được định nghĩa là cảm ứng từ khi một lực một Newton tác dụng lên một dây dẫn dài một mét có dòng điện một Ampe chạy qua, vuông góc với từ trường.
Công thức liên quan đến Tesla được biểu diễn như sau:
\[
1 \, \text{T} = \frac{1 \, \text{N}}{1 \, \text{A} \cdot 1 \, \text{m}}
\]
Bên cạnh Tesla, đơn vị Gauss (ký hiệu: G) cũng được sử dụng trong một số ngữ cảnh, đặc biệt là trong các ứng dụng kỹ thuật cũ và lĩnh vực địa vật lý. Mối quan hệ giữa Tesla và Gauss là:
\[
1 \, \text{T} = 10,000 \, \text{G}
\]
Một số đơn vị khác có liên quan đến cảm ứng từ bao gồm:
- Weber (Wb): Đây là đơn vị đo từ thông, và cảm ứng từ có thể được liên hệ với từ thông qua diện tích của bề mặt mà từ thông đi qua. Công thức được sử dụng là: \[ B = \frac{\Phi}{A} \] với \( \Phi \) là từ thông (đơn vị Weber), và \( A \) là diện tích (đơn vị mét vuông).
- Ampere trên mét (A/m): Đơn vị này được dùng để đo cường độ từ trường trong môi trường từ hóa.
Việc lựa chọn đơn vị đo phụ thuộc vào ngữ cảnh và lĩnh vực nghiên cứu cụ thể. Tesla thường được sử dụng trong các ứng dụng khoa học và công nghiệp, trong khi Gauss có thể xuất hiện trong các hệ thống cũ hoặc trong lĩnh vực địa vật lý.

5. Ứng Dụng Thực Tế Của Cảm Ứng Từ
Cảm ứng từ có nhiều ứng dụng thực tế trong đời sống hàng ngày và trong các ngành công nghiệp hiện đại. Dưới đây là một số ví dụ tiêu biểu về các ứng dụng của cảm ứng từ:
5.1. Máy Phát Điện
Máy phát điện là một trong những ứng dụng phổ biến nhất của cảm ứng từ. Khi một cuộn dây dẫn quay trong từ trường, nó tạo ra dòng điện xoay chiều thông qua hiện tượng cảm ứng điện từ. Nguyên lý này được sử dụng trong các nhà máy điện để sản xuất điện năng từ năng lượng cơ học.
5.2. Động Cơ Điện
Ngược lại với máy phát điện, động cơ điện sử dụng dòng điện để tạo ra chuyển động cơ học. Dòng điện chạy qua các cuộn dây trong động cơ tạo ra một từ trường, tương tác với từ trường của nam châm vĩnh cửu hoặc của các cuộn dây khác, làm quay rotor của động cơ.
5.3. Máy Quét MRI (Cộng Hưởng Từ)
Trong lĩnh vực y tế, máy quét MRI sử dụng từ trường mạnh để tạo ra hình ảnh chi tiết của các cơ quan và mô trong cơ thể. Nguyên lý hoạt động dựa trên việc các hạt nhân nguyên tử trong cơ thể đáp ứng với từ trường, cho phép thu thập dữ liệu để tái tạo hình ảnh chi tiết.
5.4. Cảm Biến Từ
Cảm biến từ được sử dụng rộng rãi trong các thiết bị điện tử và ô tô để phát hiện vị trí, tốc độ, và hướng chuyển động. Chúng hoạt động dựa trên việc đo lường sự thay đổi của từ trường trong môi trường xung quanh.
5.5. Ứng Dụng Trong Hệ Thống Vận Chuyển
Các hệ thống vận chuyển tiên tiến như tàu đệm từ (Maglev) sử dụng cảm ứng từ để nâng tàu lên khỏi đường ray, giảm ma sát và cho phép tàu di chuyển với tốc độ cao mà vẫn êm ái. Hệ thống này dựa trên từ trường mạnh để đạt được khả năng này.
5.6. Ổ Cứng Máy Tính
Trong lĩnh vực công nghệ thông tin, cảm ứng từ được sử dụng trong ổ cứng máy tính để lưu trữ dữ liệu. Các đĩa từ tính trong ổ cứng ghi nhận và đọc dữ liệu thông qua sự thay đổi của từ trường.
Cảm ứng từ, với khả năng tạo ra và tương tác với từ trường, có những ứng dụng sâu rộng trong nhiều lĩnh vực khác nhau, từ sản xuất năng lượng, y tế, đến công nghệ và giao thông vận tải. Điều này cho thấy tầm quan trọng và sự cần thiết của hiểu biết về cảm ứng từ trong cuộc sống hiện đại.
XEM THÊM:
6. Bài Tập Về Cảm Ứng Từ
Phần này cung cấp một số bài tập nhằm giúp bạn hiểu rõ hơn về cách tính toán cảm ứng từ trong các tình huống khác nhau. Các bài tập được phân loại từ cơ bản đến nâng cao và bao gồm cả các ứng dụng thực tế.
6.1. Bài tập cơ bản
-
Một vòng dây phẳng có diện tích \( S = 5 \, \text{cm}^2 \) được đặt trong từ trường đều có cảm ứng từ \( B = 0,1 \, \text{T} \). Góc giữa mặt phẳng vòng dây và vectơ cảm ứng từ là \( \alpha = 30^\circ \). Tính từ thông qua vòng dây.
Giải:
Áp dụng công thức từ thông: \( \Phi = B \cdot S \cdot \cos(\alpha) \)
Thay số: \( \Phi = 0,1 \cdot 5 \times 10^{-4} \cdot \cos(30^\circ) \approx 0,000433 \, \text{Wb} \)
-
Một khung dây được đặt trong từ trường đều có cảm ứng từ \( B = 0,06 \, \text{T} \). Diện tích khung dây là \( 1,2 \times 10^{-5} \, \text{m}^2 \). Tính từ thông qua khung dây khi mặt phẳng khung dây vuông góc với các đường sức từ.
Giải:
Vì khung dây vuông góc với từ trường nên \( \alpha = 0^\circ \), do đó \( \cos(0^\circ) = 1 \)
Từ thông: \( \Phi = B \cdot S = 0,06 \cdot 1,2 \times 10^{-5} = 7,2 \times 10^{-7} \, \text{Wb} \)
6.2. Bài tập nâng cao
-
Một khung dây phẳng có diện tích \( 20 \, \text{cm}^2 \), gồm 10 vòng, được đặt trong từ trường đều có độ lớn \( B = 2 \times 10^{-4} \, \text{T} \). Góc giữa vectơ cảm ứng từ và mặt phẳng khung dây là \( 30^\circ \). Tính suất điện động cảm ứng xuất hiện trong khung dây khi từ trường giảm đều về 0 trong thời gian \( 0,01 \, \text{s} \).
Giải:
Từ thông ban đầu: \( \Phi_1 = N \cdot B \cdot S \cdot \cos(\alpha) \)
Thay số: \( \Phi_1 = 10 \cdot 2 \times 10^{-4} \cdot 20 \times 10^{-4} \cdot \cos(30^\circ) \)
Từ thông cuối: \( \Phi_2 = 0 \) (vì \( B = 0 \))
Suất điện động cảm ứng: \( \epsilon = -\frac{\Delta \Phi}{\Delta t} = -\frac{\Phi_2 - \Phi_1}{0,01} \)
6.3. Bài tập ứng dụng thực tế
-
Hai dây dẫn thẳng dài song song cách nhau 32 cm đặt trong không khí. Cường độ dòng điện chạy trong dây 1 là \( i_1 = 5 \, \text{A} \) và trong dây 2 là \( i_2 = 1 \, \text{A} \), với chiều dòng điện ngược nhau. Tính cảm ứng từ tổng hợp tại điểm M nằm trong mặt phẳng chứa hai dây và cách dây 1 là 8 cm.
Giải:
Cảm ứng từ tại M do dây 1 gây ra: \( B_1 = \frac{\mu_0 \cdot i_1}{2 \pi \cdot r_1} \)
Cảm ứng từ tại M do dây 2 gây ra: \( B_2 = \frac{\mu_0 \cdot i_2}{2 \pi \cdot r_2} \), với \( r_2 = 8 + 32 = 40 \, \text{cm} \)
Cảm ứng từ tổng hợp tại M: \( B = |B_1 - B_2| \)



.jpg)

















