Chủ đề phát biểu định luật faraday lớp 11: Phát biểu định luật Faraday lớp 11 là một trong những chủ đề quan trọng trong chương trình Vật lý, giúp học sinh nắm vững nguyên lý cảm ứng điện từ và các ứng dụng rộng rãi của nó. Bài viết này sẽ cung cấp thông tin chi tiết, ví dụ minh họa và hướng dẫn giải bài tập để giúp bạn hiểu rõ và áp dụng hiệu quả định luật này.
Mục lục
Định Luật Faraday - Lớp 11
Định luật Faraday là một trong những định luật cơ bản của điện từ học, được giới thiệu trong chương trình Vật lý lớp 11. Định luật này mô tả mối quan hệ giữa sự biến thiên của từ thông và suất điện động cảm ứng được tạo ra trong mạch kín.
Phát Biểu Định Luật Faraday
Định luật Faraday phát biểu rằng:
Suất điện động cảm ứng (\(\mathcal{E}\)) sinh ra trong một mạch kín tỉ lệ thuận với tốc độ biến thiên của từ thông (\(\Phi\)) qua mạch đó.
Công thức của định luật Faraday được biểu diễn bằng:
\[
\mathcal{E} = -\frac{d\Phi}{dt}
\]
Trong đó:
- \(\mathcal{E}\) là suất điện động cảm ứng (V).
- \(\Phi\) là từ thông qua mạch (Wb).
- \(t\) là thời gian (s).
Từ Thông (\(\Phi\))
Từ thông qua một diện tích được xác định bởi:
\[
\Phi = B \cdot A \cdot \cos(\theta)
\]
Trong đó:
- \(B\) là cảm ứng từ (T).
- \(A\) là diện tích bề mặt mạch (m²).
- \(\theta\) là góc giữa vector cảm ứng từ và vector pháp tuyến của bề mặt.
Ứng Dụng Của Định Luật Faraday
Định luật Faraday có nhiều ứng dụng quan trọng trong thực tiễn, bao gồm:
- Máy phát điện: Sử dụng nguyên lý cảm ứng điện từ để biến đổi cơ năng thành điện năng.
- Máy biến áp: Điều chỉnh điện áp trong các hệ thống điện bằng cách thay đổi từ thông qua cuộn dây.
- Động cơ điện: Ứng dụng dòng điện cảm ứng để tạo ra chuyển động quay.
Ví Dụ Minh Họa
Hãy xét một cuộn dây tròn có diện tích \(A = 0,1 \, m^2\) đặt trong một từ trường đều \(B = 0,5 \, T\). Nếu từ trường tăng lên \(B = 1,0 \, T\) trong khoảng thời gian \(t = 2 \, s\), ta có:
- Từ thông ban đầu: \(\Phi_1 = B_1 \cdot A = 0,5 \cdot 0,1 = 0,05 \, Wb\).
- Từ thông cuối cùng: \(\Phi_2 = B_2 \cdot A = 1,0 \cdot 0,1 = 0,1 \, Wb\).
- Độ biến thiên từ thông: \(\Delta \Phi = \Phi_2 - \Phi_1 = 0,1 - 0,05 = 0,05 \, Wb\).
- Suất điện động cảm ứng: \(\mathcal{E} = -\frac{\Delta \Phi}{\Delta t} = -\frac{0,05}{2} = -0,025 \, V\).
Kết Luận
Định luật Faraday là nền tảng lý thuyết quan trọng để hiểu về cảm ứng điện từ, với nhiều ứng dụng trong công nghệ hiện đại như máy phát điện, máy biến áp, và động cơ điện.

.png)
I. Giới Thiệu Về Định Luật Faraday
Định luật Faraday là một trong những định luật quan trọng nhất trong lĩnh vực điện từ học, được nhà khoa học Michael Faraday phát biểu lần đầu tiên vào năm 1831. Định luật này mô tả cách một từ trường thay đổi theo thời gian có thể tạo ra một suất điện động (EMF) trong một mạch điện, hay còn gọi là hiện tượng cảm ứng điện từ.
Theo định luật Faraday, suất điện động cảm ứng trong một mạch kín tỉ lệ với tốc độ biến thiên của từ thông xuyên qua mạch đó. Công thức của định luật Faraday được biểu diễn bằng:
\[
\mathcal{E} = -\frac{d\Phi_B}{dt}
\]
Trong đó:
- \(\mathcal{E}\): Suất điện động cảm ứng (V)
- \(\Phi_B\): Từ thông qua mạch (Wb)
- \(t\): Thời gian (s)
Định luật Faraday không chỉ cung cấp nền tảng lý thuyết vững chắc cho các hiện tượng điện từ mà còn mở ra nhiều ứng dụng thực tiễn trong đời sống. Ví dụ điển hình bao gồm nguyên lý hoạt động của máy phát điện, động cơ điện, và các cảm biến từ trường.
Dưới đây là một số bước cơ bản để hiểu và áp dụng định luật Faraday:
- Xác định từ thông \(\Phi_B\) qua mạch: \(\Phi_B\) được tính bằng tích phân của từ trường \(B\) qua diện tích \(A\) mà nó xuyên qua.
- Quan sát sự thay đổi của từ thông theo thời gian \(t\).
- Áp dụng công thức của định luật Faraday để tính suất điện động cảm ứng \(\mathcal{E}\).
Với các bước này, học sinh có thể hiểu rõ hơn về bản chất của định luật Faraday và cách thức nó ảnh hưởng đến các hiện tượng điện từ trong thực tế.
II. Định Luật Faraday Về Cảm Ứng Điện Từ
Định luật Faraday về cảm ứng điện từ là một trong những nguyên lý nền tảng của vật lý điện từ, xác định mối quan hệ giữa từ trường và điện trường trong một mạch điện. Cụ thể, định luật này cho biết khi từ thông xuyên qua một mạch kín thay đổi, sẽ tạo ra một suất điện động cảm ứng trong mạch đó. Điều này có thể được mô tả bằng công thức:
\[
\mathcal{E} = -N \frac{d\Phi_B}{dt}
\]
Trong đó:
- \(\mathcal{E}\): Suất điện động cảm ứng (V)
- \(N\): Số vòng dây trong cuộn dây
- \(\Phi_B\): Từ thông qua mạch (Wb)
- \(t\): Thời gian (s)
Định luật Faraday về cảm ứng điện từ không chỉ giải thích cơ chế sinh ra suất điện động cảm ứng mà còn giải thích nguyên lý hoạt động của các thiết bị như máy phát điện, động cơ điện và các loại cảm biến từ.
Dưới đây là các bước cụ thể để áp dụng định luật Faraday trong việc tính toán suất điện động cảm ứng:
- Xác định từ thông \(\Phi_B\) qua mạch: Từ thông được tính bằng tích phân của từ trường \(B\) qua diện tích \(A\) mà nó xuyên qua.
- Theo dõi sự biến thiên của từ thông \(\Phi_B\) theo thời gian \(t\).
- Áp dụng công thức \(\mathcal{E} = -N \frac{d\Phi_B}{dt}\) để tính suất điện động cảm ứng trong mạch.
Với các kiến thức này, học sinh có thể hiểu rõ cách định luật Faraday giải thích sự tương tác giữa từ trường và điện trường, đồng thời vận dụng định luật này trong các bài tập và ứng dụng thực tế.

III. Định Luật Faraday Về Điện Phân
Định luật Faraday về điện phân là một định luật quan trọng trong hóa học và điện học, giúp giải thích mối quan hệ giữa lượng điện tích truyền qua một dung dịch điện phân và lượng chất được giải phóng hoặc tích tụ tại các điện cực. Định luật này được Michael Faraday phát biểu vào năm 1834, dựa trên các thí nghiệm của ông về hiện tượng điện phân.
Có hai định luật Faraday về điện phân:
- Khối lượng của chất được giải phóng ở điện cực (hoặc tích tụ) tỉ lệ thuận với lượng điện tích \(Q\) truyền qua dung dịch:
\[
m = k \cdot Q
\]
- \(m\): Khối lượng của chất được giải phóng (g)
- \(Q\): Lượng điện tích (Coulomb)
- \(k\): Hằng số tỉ lệ, phụ thuộc vào chất điện phân và bản chất của ion.
- Khối lượng của chất được giải phóng tỉ lệ thuận với đương lượng điện hóa của chất đó:
\[
m = \frac{E \cdot Q}{F}
\]
- \(E\): Đương lượng điện hóa của chất (g/Coulomb)
- \(F\): Hằng số Faraday, bằng \(96485\) Coulomb/mol.
Để áp dụng định luật Faraday về điện phân vào thực tế, ta có thể thực hiện theo các bước sau:
- Xác định lượng điện tích \(Q\) truyền qua dung dịch điện phân bằng cách nhân cường độ dòng điện \(I\) với thời gian \(t\) điện phân: \[Q = I \cdot t\]
- Sử dụng công thức \(m = \frac{E \cdot Q}{F}\) để tính khối lượng của chất được giải phóng hoặc tích tụ tại các điện cực.
Với các công thức và phương pháp trên, định luật Faraday về điện phân không chỉ giải thích cơ chế của quá trình điện phân mà còn cung cấp công cụ mạnh mẽ để tính toán các quá trình điện hóa trong công nghiệp và nghiên cứu.

XEM THÊM:
IV. So Sánh Giữa Định Luật Faraday Về Cảm Ứng Điện Từ Và Điện Phân
Định luật Faraday về cảm ứng điện từ và định luật Faraday về điện phân đều là những phát hiện quan trọng trong vật lý, nhưng chúng liên quan đến những hiện tượng khác nhau và có những điểm tương đồng cũng như khác biệt đáng chú ý. Dưới đây là sự so sánh chi tiết giữa hai định luật này:
1. Điểm Giống Nhau
- Cả hai định luật đều do Michael Faraday phát hiện và mang tên ông.
- Đều liên quan đến hiện tượng điện từ, trong đó có sự tương tác giữa từ trường và điện trường.
- Cả hai định luật đều có các ứng dụng rộng rãi trong khoa học và công nghệ, từ việc phát điện đến quá trình điện phân trong công nghiệp.
2. Điểm Khác Nhau
| Tiêu Chí | Định Luật Faraday Về Cảm Ứng Điện Từ | Định Luật Faraday Về Điện Phân |
|---|---|---|
| Hiện Tượng | Cảm ứng điện từ, suất điện động sinh ra do sự thay đổi từ thông. | Điện phân, quá trình chuyển hóa năng lượng điện thành hóa năng. |
| Công Thức | \(\mathcal{E} = -N \frac{d\Phi_B}{dt}\) | \(m = \frac{E \cdot Q}{F}\) |
| Ứng Dụng | Máy phát điện, biến áp, động cơ điện, cảm biến từ. | Điện phân kim loại, sản xuất hóa chất, mạ điện. |
| Bản Chất | Liên quan đến sự biến đổi của từ trường và sự cảm ứng suất điện động. | Liên quan đến dòng điện chạy qua dung dịch điện phân và sự tích lũy hoặc giải phóng chất tại điện cực. |
Sự so sánh này cho thấy rằng, mặc dù cùng được phát biểu bởi Michael Faraday, hai định luật này lại khám phá những khía cạnh khác nhau của hiện tượng điện từ, và đều có tầm quan trọng riêng biệt trong vật lý cũng như trong các ứng dụng thực tiễn.

V. Bài Tập Vận Dụng Định Luật Faraday
Để hiểu rõ hơn về định luật Faraday và áp dụng vào các tình huống thực tế, học sinh cần thực hành qua các bài tập đa dạng. Dưới đây là một số bài tập vận dụng định luật Faraday về cảm ứng điện từ và điện phân, cùng với các bước hướng dẫn chi tiết:
1. Bài Tập Về Cảm Ứng Điện Từ
Bài tập 1: Một cuộn dây gồm 200 vòng dây có diện tích mặt cắt ngang là 0,01 m2. Từ thông qua cuộn dây biến thiên đều từ 0,5 Wb xuống 0 Wb trong 0,1 giây. Tính suất điện động cảm ứng sinh ra trong cuộn dây.
Lời giải:
- Xác định số vòng dây: \( N = 200 \)
- Xác định từ thông ban đầu và cuối cùng: \(\Phi_{B1} = 0,5 \, \text{Wb}\), \(\Phi_{B2} = 0 \, \text{Wb}\)
- Tính sự thay đổi của từ thông: \(\Delta \Phi_B = \Phi_{B2} - \Phi_{B1} = 0 - 0,5 = -0,5 \, \text{Wb}\)
- Tính suất điện động cảm ứng: \[ \mathcal{E} = -N \frac{\Delta \Phi_B}{\Delta t} = -200 \cdot \frac{-0,5}{0,1} = 1000 \, \text{V} \]
Vậy suất điện động cảm ứng sinh ra trong cuộn dây là 1000 V.
2. Bài Tập Về Điện Phân
Bài tập 2: Điện phân dung dịch CuSO4 với cường độ dòng điện 5 A trong thời gian 30 phút. Biết đương lượng điện hóa của Cu là 0,0003294 kg/C. Tính khối lượng đồng giải phóng tại catot.
Lời giải:
- Tính tổng lượng điện tích truyền qua dung dịch: \[ Q = I \cdot t = 5 \, \text{A} \cdot 1800 \, \text{s} = 9000 \, \text{C} \]
- Tính khối lượng đồng giải phóng: \[ m = E \cdot Q = 0,0003294 \, \text{kg/C} \cdot 9000 \, \text{C} = 2,9646 \, \text{g} \]
Vậy khối lượng đồng được giải phóng tại catot là 2,9646 g.
Qua các bài tập trên, học sinh có thể nắm vững cách áp dụng định luật Faraday trong cả hai lĩnh vực cảm ứng điện từ và điện phân, từ đó củng cố kiến thức và chuẩn bị tốt hơn cho các kỳ thi.
VI. Kết Luận
Định luật Faraday là một trong những nền tảng của vật lý điện từ và hóa học, mở ra nhiều hướng nghiên cứu và ứng dụng thực tiễn quan trọng. Từ việc hiểu được cách mà từ trường có thể sinh ra điện trường cho đến việc khám phá quá trình điện phân, định luật này đã chứng minh sự kết nối sâu sắc giữa các hiện tượng tự nhiên.
Trong quá trình học tập và vận dụng định luật Faraday, học sinh không chỉ nắm vững các khái niệm lý thuyết mà còn phát triển khả năng giải quyết các bài toán thực tế. Điều này góp phần không nhỏ vào việc hình thành tư duy khoa học và khả năng ứng dụng kiến thức vào cuộc sống, từ việc thiết kế các thiết bị điện tử đến sản xuất công nghiệp.
Để kết thúc, có thể khẳng định rằng việc hiểu và áp dụng định luật Faraday không chỉ là một phần thiết yếu của chương trình vật lý lớp 11 mà còn là bước chuẩn bị quan trọng cho những nghiên cứu sâu hơn trong lĩnh vực khoa học và công nghệ.
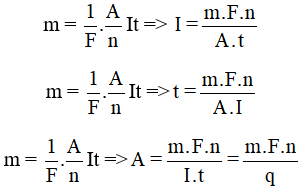
.jpg)






















